Вопрос 14 Результат решения уравнения Шредингера для атома водорода

Атом водорода представляет собой систему, состоящую из элек­трона, который обращается в кулоновском поле ядра (протона). Потенциальная энергия такой системы не зависит от времени и равна:

.

Эту величину следует подставить в стационарное уравнение Шредингера (6) и решить его с учетом стандартных условий, накла­дываемых на волновую функцию. Так как силовое поле, создаваемое ядром, сферически симметрично, то решать эту задачу удобнее в сферических координатах . Результат решения сводится к следующему. Уравнение решается только при определенных, образующих дискретный ряд, значениях параметра :

(7)

где m и e – масса и заряд электрона, n = 1,2,3....

Эти значения и являются возможными (разрешенными) значениями энергии атома водорода. Возможные волновые функции электрона в атоме водорода могут быть записаны в виде произведения трех составляющих, каждая из которых зависит от одной из координат сферической системы

(8)

где – так называемый первый боровский радиус, равный

.

Уравнение Шредингера решается функциями (8) лишь при определенных значениях чисел n, l, m, которые взаимосвязаны следующим образом:

(9)

Значения коэффициентов и в выражении (8) находятся для каждого состояния исходя из условия нормировки (3), которое в сферических координатах распадается на три условия:

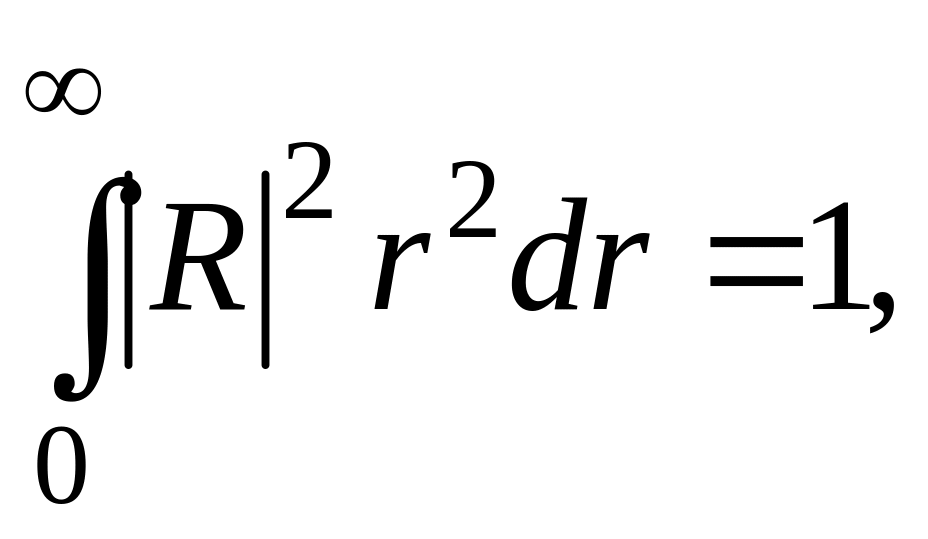
(10)

Возьмем, например, . Энергия атома в этом случае минимальна (основное состояние) и равна

эВ.

Остальные два квантовых числа l и m могут иметь только нуле­вые значения и энергии соответствует только одна волновая функция (вырождение отсутствует).

При квантовое число l может принимать значения 0 и 1, причем при , а при . В конечном счете значению соответствуют четыре различных состояния, описываемые волновыми функциями и каждому из них соответствует одна и та же энергия (четырех­кратное вырождение). Схематично:

Аналогично, при возможны 9 состояний, описываемых волновыми функциями:

и во всех этих состояниях атом обладает одной и той же энергией (девятикратное вырождение).

Рассмотрим конкретный вид нескольких первых волновых функций.

1. . Подставляя эти значения в (8), получим:

(11)

Применение условий нормировки дает:

Подставляя эти значения в (11), получим волновую функцию основного (невозбужденного) состояния атома водорода

(12)

Так как эта функция не зависит от углов и (сферически симметрична), то вероятность обнаружить электрон на данном рас­стоянии от, ядра будет одинакова по всем направлениям. Най­дем вероятность нахождения электрона в пределах элементарного слоя, ограниченного сферами радиусами и (рис.1).

Р и с. 1

Объем этого слоя и соответствующая вероятность, согласно (1) и (12), запишется:

Введем радиальную плотность вероятности следующим образом:

(13)

Графически эта функция изображается кривой, приведенной на рис. 2. Максимум кривой при свидетельствует о том, что для атома водорода, находящегося в основном состоянии, наиболее вероятное удаление электрона от ядра соответствует первому боровскому радиусу.

2. При для волновой функции, согласно (8) при учете (10) можно получить

             

         (r)

Р и с. 2

Эта функция также сферически симметрична, поэтому и здесь естес­твенно ввести радиальную плотность вероятности, которая запишет­ся следующим образом

(14)

3. При волновая функция имеет вид:

(15)

4. При

(16)

5. При

Если вероятность нахождения электрона в сферическом слое толщиной , удаленном на расстоянии от ядра, равна , то величина, введенная как называется радиальной плотностью вероятности. Если зависимость задана графически, то величина определяется как площадь прямоугольника с основа­нием и высотой , восстановленного на расстоянии от начала координат (площадь заштрихованного прямоугольника).