Вопрос 6 Опыты Штерна и Герца. Вопрос 16 , 19 Спин электрона.

Из опытов Штерна и Герлаха следует, что величина спинового магнитного момента равна магнетону Бора:

Следовательно, отношение магнитного спинового момента к механи­ческому спиновому моменту равно

Это означает, что отношение магнитного спинового момента к спину в два раза больше гиромагнитного отношения . Такой резуль­тат согласуется также с результатами других опытов, в частности, с опытами Эйнштейна – де Гааза и с опытами Барнета по определению гиромагнитного отношения. Дальнейшие эксперименты показали, что g – фактор для электрона немного больше двух : g=2(1+α). Это связывают с аномальным магнитным моментом электрона. Согласно теории α = 0,001159614(±3). В экспери­менте было получено значение α = 0,001159557(±30). Были проведены также прямые эксперименты, которые непосредственно доказали, что спин является собственной характеристикой электро­на, а не характеристикой электронов как составных частей атома.

5. Спин, наряду с зарядом и массой, относится к числу фунда-­ ментальных характеристик электрона. Но спин не является исключи­- тельным свойством электрона. Спином характеризуются все частицы микромира, при этом спиновое квантовое число может быть различным. Существуют частицы, для которых спиновое квантовое число является полуцелым. Это – электрон, протон, нейтрон и др. Такой класс час­тиц называют фермионами. Есть частицы с целым спином, включая нуль. Такой класс частиц называют бозонами. Например, спин фотона равен единице, спин альфа–частицы равен нулю и т.д.

6. Спину, как и всякой физической величине, сопоставляется соответствующий оператор спина, и может быть поставлена задача на его собственные значения. Однако эти вопросы выходят за рамки данного курса.

Вопрос 7 Развитие взглядов на природу света. Эффект Комптона

Хорошо известно, что существует широкий класс явлений, в которых электромагнитное излучение взаимодействует с заряженными частицами. Мы рассмотрим одно из этих явлений, получившее название эффекта Комптона, поскольку в нем особенно ярко демонстрируются недостаточность волновой теории и корпускулярные свойства света.

В 1923 г. американский физики А.Комптон, исследуя рассеяние рент­геновского излучения различными веществами, обнаружил, что в нем наряду с излучением первоначальной длины волны λ₀ содержится также излучение с большей длиной λ.

Разность Δλ = λ – λ₀, получившая название комптоновского сдвига, оказалась зависящей только от угла θ между направле­ниями рассеянного и первичного лучей. Сдвиг Δλ от длины волны λ₀ и от природы рассеивателя не зависит и определяется формулой

, (1.1.1)

где измеренное экспериментальное значение постоянной λ_С оказа­лось равным 2,43·10^–2 нм.

Из того факта, что Δλ не зависит от природы рассеивающего вещества, с несомненностью следует, что рассеяние лучей происходит не на атомах, а на электронах мишени. С точки зрения классического волнового описания механизм рассеяния состоит в следующем: электри­ческое поле падающей волны с частотой ω "раскачивает" электроны в мишени с той же самой частотой. При этом электроны излучают, подобно элементарному диполю, вторичные волны с той же самой час­тотой симметрично относительно плоскости, нормальной к направлению первичного излучения. Таким образом, в классической волновой картине рассеянное излучение независимо от угла рассеяния должно обладать одной и той же частотой - частотой ω₀ падающей волны. Этот результат противоречит эксперименту, что говорит о недостаточности волнового описания рассеяния света очень коротких длин волн на веществе.

Комптон интерпретировал свои экспериментальные результаты, постулировав, что падающее на мишень рентгеновское излучение должно опи­сываться не как волна с частотой ω₀, а как поток квантов, каждый с энергией . Процесс рас­сеяния в этой модели представляет собой упругое столкновение фотона со свободным покоящимся электроном вещества. Налетающий фотон переда­ет при столкновении часть своей энергии электрону, поэтому рассеянный квант обладает меньшей энергией Е, а, следовательно, рассеян­ное излучение - меньшей частотой .

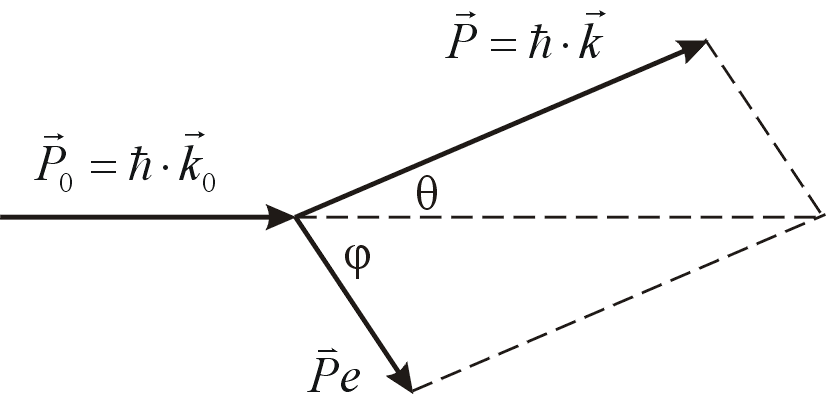
рис. 1.1

Изложим аргументы в пользу модели свободного и покоящегося до рассеяния электрона мишени. Справедливость этих предположений сле­дует из того, что энергия рентгеновского кванта (десятки килоэлектрон-вольт) на несколько порядков превосходит энергию связи электрон в атоме. Условие, при выполнении которого электрон может считаться покоящимся и свободным, достаточно очевидно: энергия, переданная электрону в акте рассеяния, должна значительно превосходить как его кинетическую энергию, так и энергию связи в атоме. Наиболее слабо связанные электроны внешних оболочек атомов (кинетическая энергия и энергия связи порядка нескольких электрон-вольт) заведомо удов­летворяют этому условию.

Импульсы фотона до и после рассеяния составляют соответственно

и , (1.1.2)

где ω₀, ω и k₀, k – соответственно частоты и волновые числа па­дающей и рассеянной волн. Поскольку фотон летит в направлении рас­пространения электромагнитной волны, направление его импульса совпадает с . Следовательно, соотношения (1.1.2) можно представить в векторной форме:

и (1.1.3)

На рис. 1.1 изображена диаграмма импульсов для упругого столкновения фотона со свободным покоящимся до столкновения электроном. Здесь – импульс налетающего фотона; – им­пульс фотона, рассеянного под углом θ; φ и – угол вылета и импульс электрона отдачи.

До столкновения импульс электрона равен нулю, а его энер­гия равна , где – инвариантная масса электрона ("масса покоя" частицы). После столкновения электрон приобретает импульс и энергию (так как в общем слу­чае скорость электрона отдачи значительна, мы используем реляти­вистские формулы).

Из законов сохранения энергии и импульса системы следуют два равенства:

(1.1.4)

(1.1.5)

Разделим обе части равенства (1.1.5) на с и перегруппируем члены:

.

Возведение этой формулы в квадрат даст

.

В равенстве (1.1.5) перенесем налево слагаемое и возведем в квадрат обе части получившегося при этом уравнения:

(1.1.7)

где θ – угол между и . Из сравнения (1.1.6) и (1.1.7) по­лучим

Умножим обе части этого равенства на 2π и разделим на . В итоге найдем, что

(1.1.8)

Если теперь учесть, что из (1.1.8) последует формула

(1.1.9)

где величину

(1.1.10)

называют комптоновской длиной волны той частицы, масса m кото­рой фигурирует в формуле. В рассматриваемом нами явлении λ_С – комптоновская длина волны электрона: . Подстановка в опре­делении (1.1.10) числовых значений и с дает для электрода значение λ_С = 2,43·10^–2 нм, совпадающее с экспериментальным.

Таким образом, в рамках корпускулярного описания электромаг­нитного излучения мы получили одну из основных закономерностей эффекта Комптона, выражаемую формулой (1.1.1). Обратим внимание на то, что в пределе h→0 комптоновская длина волны λ_С части­цы, а следовательно, и комптоновский сдвиг Δλ обращаются в нуль, что совпадает с выводом классической теории. Такое совпадение не случайно и в дальнейшем нам не раз придется столкнуться с формаль­ным переходом результатов квантовой механики в результаты класси­ческой при h→0. Отсюда следует важный вывод о том, что наличие в некотором выражении постоянной Планка является характерным приз­наком его "квантово-механической природы". Так, в частности, эф­фект Комптона представляет собой сугубо квантовое явление.

За открытие и объяснение эффекта А.Комптон был удостоен Нобелевской премии по физике в 1927 г.

Вопрос 8 – 9 Корпускулярно – волновой дуализм, Экспериментальное подтверждение гипотезы де Бройля: опыт Дэвиссона и Джермера, опыт Штерна, Гипотеза де Бройля. Уравнения волны де Бройля для свободной частицы.

Идея де Бройля заключалась в том, чтобы расширить аналогию между оптикой и механикой и волновой оптике сопоставить волновую механику, попытавшись применить последнюю к внутриатомным явлениям. "Попытка приписать электрону, и вообще всем частицам, подобно фотонам, двойственную природу, наделить их волновыми корпускуляр­ными свойствами, связанными между собой квантом действия (постоян­ной Планка ), – такая задача представлялась крайне необхо­димой и плодотворной... Необходимо создать новую механику волново­го характера, которая будет относиться к старой механике как вол­новая оптика к геометрической оптике", – писал де Бройль в книге "Революция в физике".

За открытие волновых свойств вещества Л. де Бройль в 1929 г. был удостоен Нобелевской премии.

Обратимся теперь к формальной стороне вопроса. Пусть мы имеем микрочастицу (например, электрон) с массой m, движущуюся в вакууме с постоянной скоростью . Пользуясь корпускулярным описанием, припишем частице энергию E и импульс в соответствии с формулами (рассмотрим общий случай релятивистской частицы).

. (1.2.1)

С другой стороны, в волновой картине мы используем понятия частоты и длины волны (или волнового числа ). Если оба описания являются различными аспектами одного и того же физическо­го объекта, то между ними должна быть однозначная связь. Следуя де Бройлю, перенесем на случай частиц вещества те же правила пере­хода от одной картины к другой, справедливые в применении к све­ту:

(1.2.2)

Соотношения (1.2.2) получили название формул де Бройля. Длина волны, связанная с частицей, определяется выражением

(1.2.3)

ее называют длиной волны де Бройля. Нетрудно сообразить по аналогии со светом, что именно эта длина волны должна фигурировать в критериях применимости волновой или корпускулярной картин.

Наиболее простым типом волны в вакууме с определенной часто­той и волновым вектором является плоская монохроматическая волна

Поэтому в соответствии с формулами (1.2.2) свяжем с движением час­тицы волну вида

(1.2.4)

Такую волну называют волной де Бройля. Непростой вопрос о физической природе этой волны и о толковании ее значений отложим на последующие параграфы.

Из определения (1.2.3) получим ряд полезных соотношений, свя­зывающих длину волны де Бройля с параметрами движущейся частицы. Подставив формулу (1.2.1) для импульса частицы p в (1.2.3), полу­чим зависимость от скорости частицы:

(1.2.5)

Выразив с помощью соотношения импульс час­тицы p через ее полную энергию E, найдем, что

(1.2.6)

Обозначим T кинетическую энергию частицы. Воспользовавшись определением , из (1.2.6) получим формулу

(1.2.7)

выражающую дебройлевскую длину волны частицы через ее кинетичес­кую энергию.

В предельном случае нерелятивистской частицы, когда отноше­ние , из (1.2.6) получим выражение для дебройлевской длины волны в нерелятивистском приближении:

(1.2.8)

Разумеется, выражение (1.2.8) можно было получить непосредственно из формулы (1.2.5) в пределе, когда отношение .

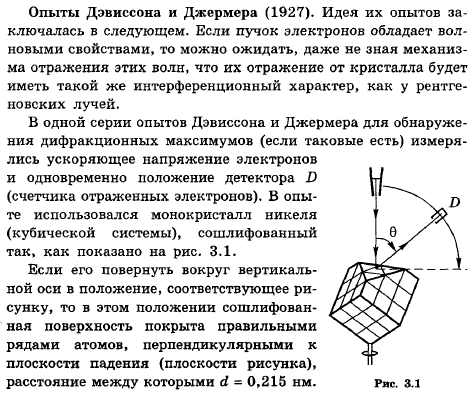
Экспериментальное подтверждение гипотезы де Бройля: опыт Дэвиссона и Джермера, опыт Штерна.