Вопрос 2 Явления подтверждающие сложность строения атома. Закономерности в атомных спектрах. Формула Бальмера

Изучение атомных спектров послужило ключом к познанию строе­ния атома. Прежде всего, было замечено, что линии в спектрах атомов располагается не беспорядочно, а группируется в так на­зываемые серии. Отчетливее всего это обнаруживается в спектре атома водорода, изображенном на рис. 1.

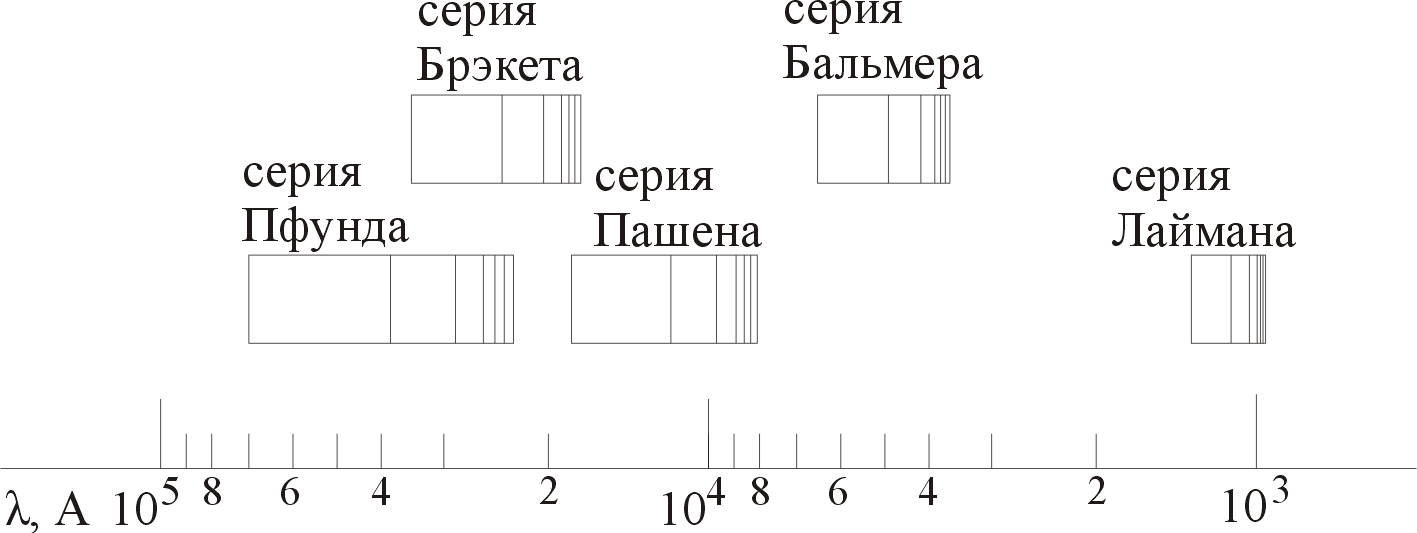
Р и с. 1

Очевидно, что линии располагаются в определенном порядке в виде серий, а расстояние между линиями в каждой серии закономерно убывает по мере перехода от более длинных волн к более коротким. Швейцарский физик Иоганн Бальмер обнаружил (1885 г.), что длины волн линий водорода могут быть точно представлены формулой

(1)

или, при переходе от длины волны к частоте,

, (2)

где R = 109737 см^-1 (3)

 эмпирическая постоянная, называемая постоянной Ридберга, с  скорость света в вакууме.

С формул (1) и (2) можно получить λ или  любой линии в любой серии. Так, если положить n₂ = 1, а величине n₁ прида-

вать значения 2,3,4,... , то получим длины волн (частоты) линий в серии Лаймана:

серия Лаймана: n₂ = 1, n₁ = 2,3,4 ... (ультрафиолетовая область)

Аналогично, линии остальных серий получаются при следующих значениях n₂ и n₁:

серия Бальмера: n₂ = 2, n₁ = 3,4,5 ... (видимая область)

серия Пашена: n₂ = 3, n₁ = 4,5,б... (инфракрасная область)

серия Брэкета: n₂ = 4, n₁ = 5,6,7 (инфракрасная область)

серия Пфунда: n₂ = 5, n₁ = б,7,8 ... (инфракрасная область)

Вопрос 5 Ядерная модель атома (атом Резерфорда). Заряд атома.

Вопрос 6 Постулаты Бора, Опыты Франка и Герца, Квантование эллиптических орбит атом бора

Первая удачная попытка создания модели атома водорода, кото­рая объяснила его наблюдаемый спектр, принадлежит Нильсу Бору (1913 г.). В конечном счете, Бор исходил из трех постулатов, которые можно сформулировать следующим образом:

1. Атомы могут пребывать только в определенных стационарных состояниях, в которых они не излучают и не поглощают энергии. В этих со­стояниях атомы обладают энергиями, образующими дискретный ряд:

Е₁, Е_2, Е_3, Е_4… (4)

2. Атомы могут излучать или поглощать энергию лишь при пере­ходе из одного стационарного состояния в другое, причем частоты излучения (поглощения) определяются правилом:

(5)

3. В стационарных состояниях электрон движется вокруг ядра по круговым орбитам, для которых момент импульса электро­на принимает значения, кратные :

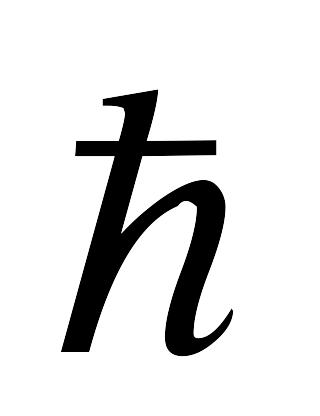, n = 1,2,3,4… (6)

где h и =h/2 – постоянные Планка.

По выражение самого Бора, "эти допущения находятся в явном противоречии с общепринятым пониманием электродинамики, но представляются необходимыми для экспериментально установленных фактов".

Если учесть, что момент импульса по определению или просто N = mVr для круговых орбит, то, используя третий постулат, можно, найти радиусы разрешенных орбит

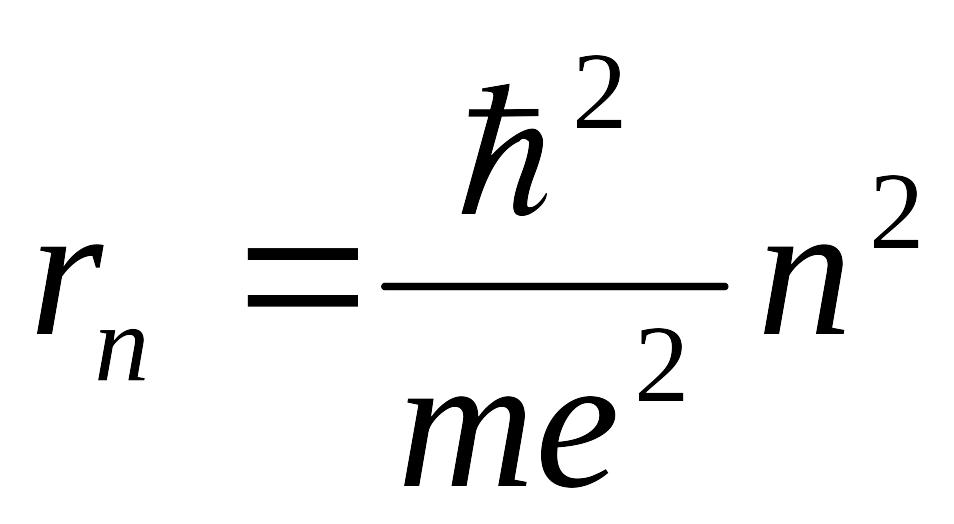, (7)

где m – масса и e – заряд электрона.

Далее, имея в виду, что полная энергия атома как системы ядро-электрон связана с ради­усом обращения электрона как E = –е²/2r, можно получить выражение для возможных значений энергий атома в стационарных состояниях:

(8)

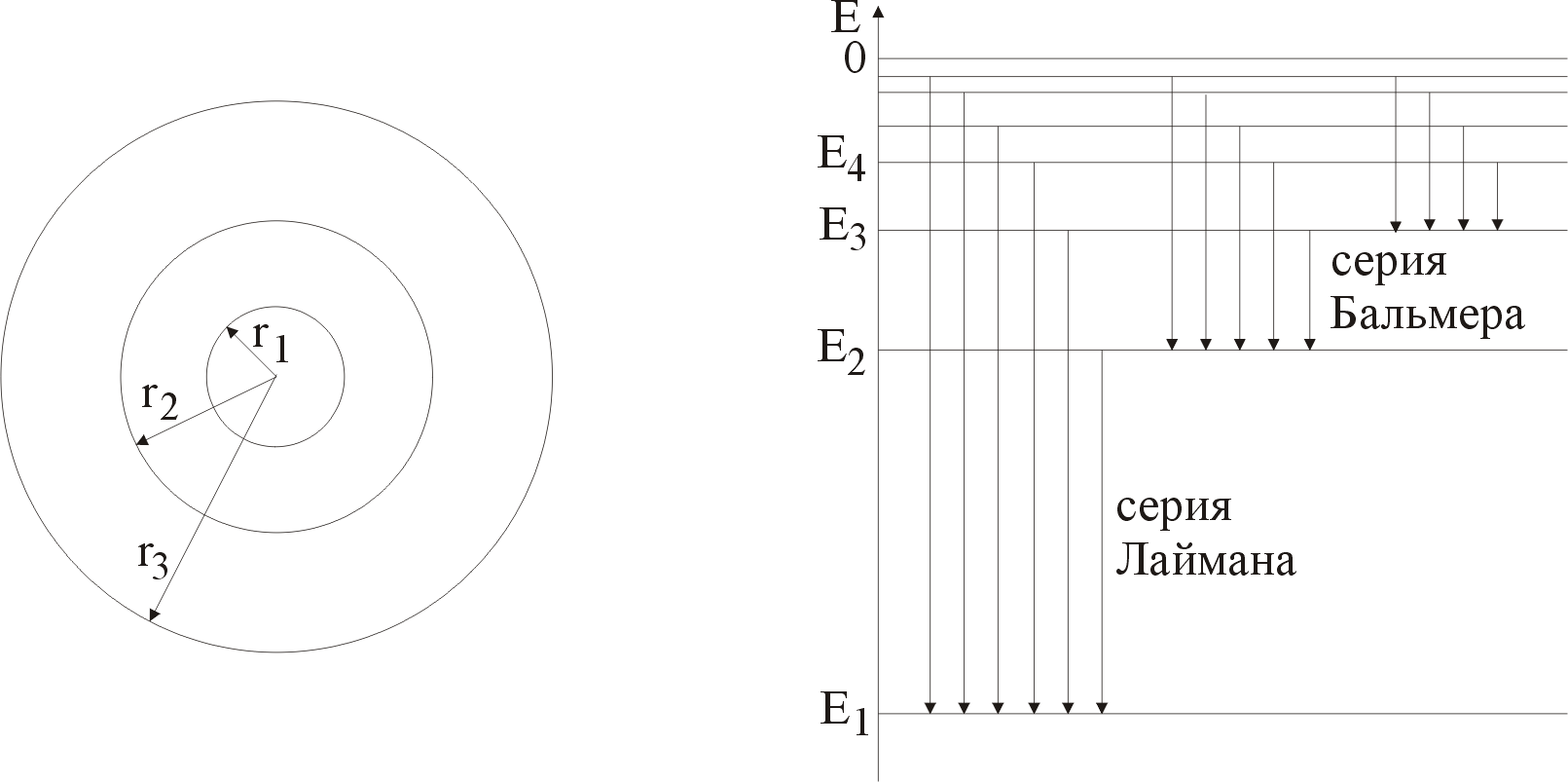
На рис. 2 графически изображены возможные значения энергии и соответствующие орбиты электронов в атоме водорода.

а) б)

Р и с. 2

Основно­му (невозбужденному) состоянию при n = 1 соответствуют:

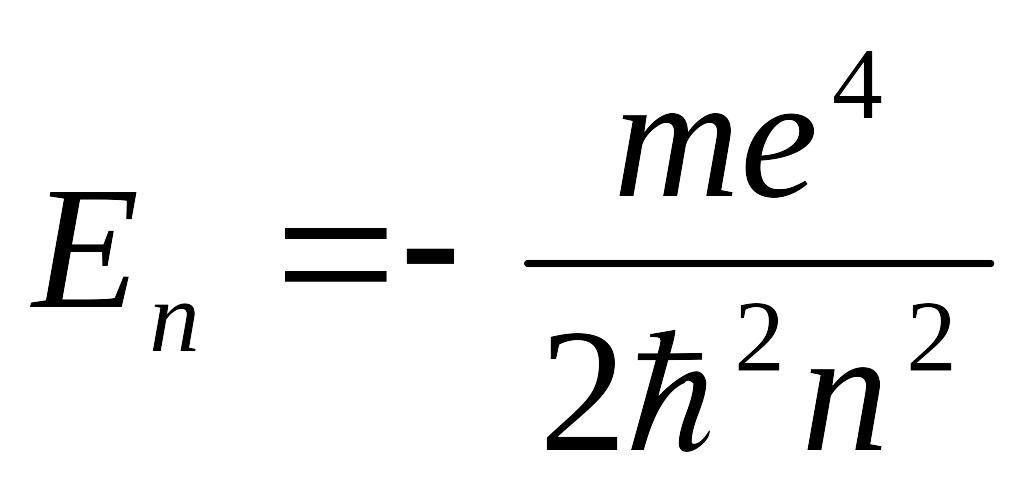= –13,6 эВ и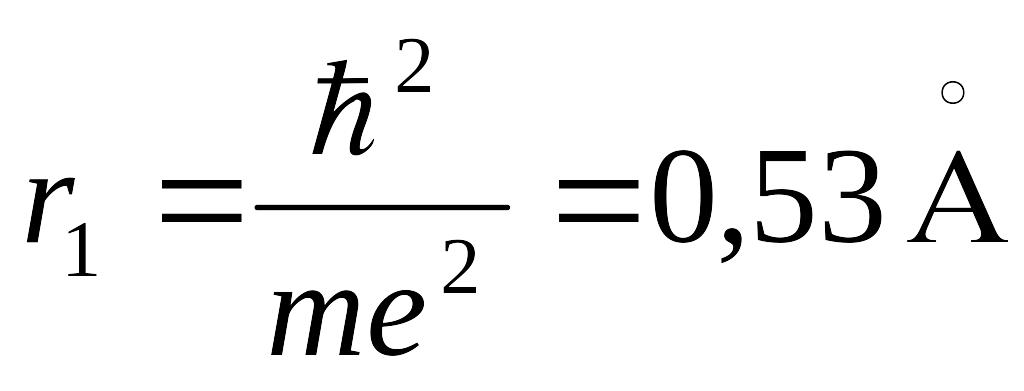

где r₁  так называемый первый боровский радиус.

При возбуждении атомы переходят в состояния c большими зна­чениями энергии и затем, при обратных переходах, которые изо­бражены стрелками и сгруппированы определенным образом на ри­с. 2,б, излучают, согласно правилу частот (5), серии линий, изображенные на рисунке 1.

Аналитически частоты этих линий можно получить, комбинируя (5) и (8)

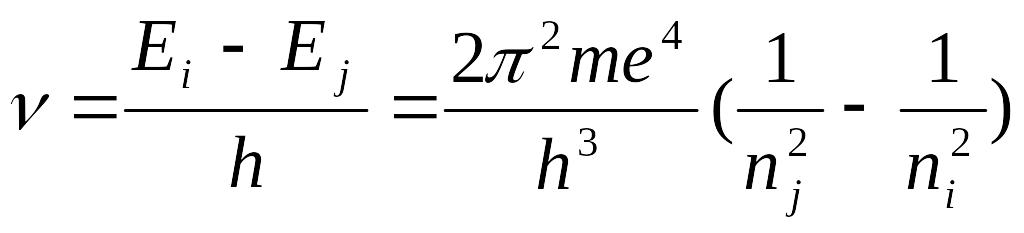(9)

С точностью до принятых обозначений (9) соответствует выраже­нию (2), в котором с таким же успехом можно было принять n₂ = n_j и n₁ = n_i. Приравнивая коэффициенты перед скобками в (2) и (9), можно выразить постоянную Ридберга через универ­сальные константы и получить ее значение:

см^-1,

что поразительно хорошо согласуется с эмпирическим значением (3), Таким образом, выражения (2) и (9) совершенно эквивалент­ны, что свидетельствует о полном количественном соответствии теории Бора с экспериментом.

Опыты Франка и Герца.

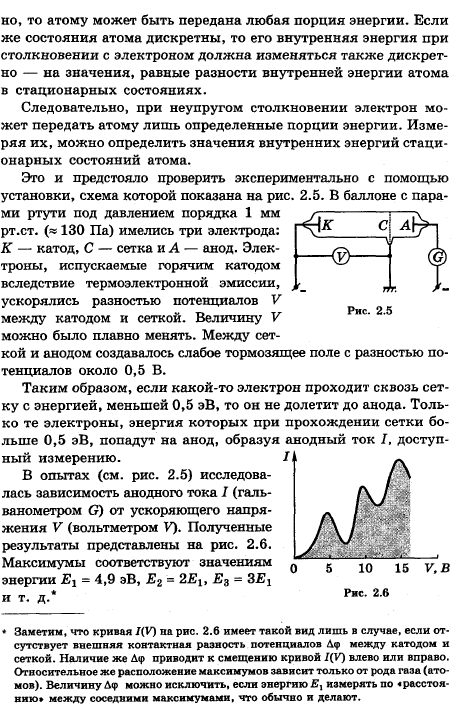
Квантование эллиптических орбит