
- •1. Основные понятия и принципы исследования операций
- •2. Типичные задачи исследования операций
- •3. Понятие модели и моделирования
- •4. Виды моделирования. Различные модели исследования операций
- •5. Основная задача линейного программирования.
- •7. Задача о снабжении сырьем
- •8. Сведение произвольной задачи линейного программирования к основной
- •9.Использование электронных таблиц при решении задач линейной оптимизации.
- •10.Графическое решение задач линейного программирования
- •11.Ключевая идея дп. Принцип оптимальности Беллмана.
- •12. Решение задачи о распределении ресурсов методами динамического программирования
- •13.Моделирование случайных чисел.
- •14. Вычисление определенного интеграла методом Монте-Карло
- •15. Нахождение площади геометрической фигуры методом Монте-Карло
- •16. Основные понятия и определения теории графов
- •17. Способы задания графа. Матрицы смежностей и инциденций.
- •18. Графы типа дерево. Остовное дерево. Минимальное остовное дерево
- •19. Задачи оптимизации на графах. Алгоритм Краскала построения минимального остовного дерева
- •20. Сетевое планирование: основная идея и модели решаемых задач
- •21. Моделирование систем массового обслуживания
- •22.Моделирование смо: каналы ,очереди, дисциплины обслуживания.
10.Графическое решение задач линейного программирования
 Среди
всех точек выпуклой области, являющейся
решением системы ограничений, выбрать
такую, координаты которой минимизируют
(максимизируют) линейную функцию F
= с1x + с2y.
Заметим, что переменные x,
y в ЗЛП
принимают, как правило, неотрицательные
значения (x≥
0, y ≥ 0),
поэтому область расположена в 1 четверти
координатной плоскости. Рассмотрим
линейную функцию F
= с1x + с2y и
зафиксируем какое-нибудь ее значение
F.
Пусть, к примеру, F
= 0,
т.е. с1x + с2y
= 0. Графиком
этого уравнения будет прямая, проходящая
через начало координат (0;0).
При изменении фиксированного значения
F =
d,
прямая с1x+
с2y = d
будет
смещаться параллельно и «зачертит» всю
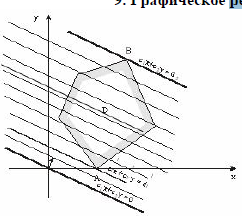
плоскость. Пусть D
–
многоугольник – область решения системы
ограничений. При изменении d
прямая
с1x + с2y = d,
при некотором
значении d
= d1 достигнет
многоугольника D,
назовем эту точкуА«точкой
входа», и затем, пройдя многоугольник,
при некотором значении d
= d2 будем
иметь с ним последнюю общую точку В,
назовем В
«точкой
выхода». Очевидно, что своего наименьшего
и наибольшего значения целевая функция
F = с1x + с2y
достигнет
в точках «входа» А
и «выхода»
В.
Учитывая,
что оптимальное значение на множестве
допустимых решений целевая функция
принимает в вершинах области D,
можно предложить следующий алгоритм
решения задачи двумерного линейного
программирования графическим
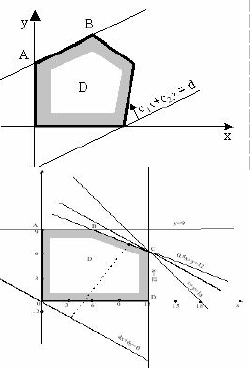
методом.1)Строим
область допустимых решений функции
F.Для
этого в ограничениях знаки неравенства
заменяем знаками равенства и строим
полученные прямые. Затем определяем те
полуплоскости, которые соответствуют
данным ограничениям и получаем область
допустимых решений, лежащую на пересечении
всех полуплоскостей.»2)Строим
прямую уровня.Для
этого берём произвольную точку М,
принадлежащую области допустимых
решений функции F
и, подставив координаты этой точки в
функцию, получаем прямую уровня. Затем
от выбранной точки М, откладываем вектор
а, координаты которого – это коэффициенты
при целевой функции F.
3)Максимализируем
(минимизируем) целевую функцию F.
Для максимизации
(минимизации)функции F
передвигаем прямую уровня по направлению
(в обратном направлении относительно)
вектора а до пересечения с граничной
точкой области допустимых решений.
Полученная точка является оптимальным
решением, в котором функция достигает
свой максимум (минимум). Находим координаты
этой точки и представляем их в функцию
F.
Среди
всех точек выпуклой области, являющейся
решением системы ограничений, выбрать
такую, координаты которой минимизируют
(максимизируют) линейную функцию F
= с1x + с2y.
Заметим, что переменные x,
y в ЗЛП
принимают, как правило, неотрицательные
значения (x≥
0, y ≥ 0),
поэтому область расположена в 1 четверти
координатной плоскости. Рассмотрим
линейную функцию F
= с1x + с2y и
зафиксируем какое-нибудь ее значение
F.
Пусть, к примеру, F
= 0,
т.е. с1x + с2y
= 0. Графиком
этого уравнения будет прямая, проходящая
через начало координат (0;0).
При изменении фиксированного значения
F =
d,
прямая с1x+
с2y = d
будет
смещаться параллельно и «зачертит» всю
плоскость. Пусть D
–
многоугольник – область решения системы
ограничений. При изменении d
прямая
с1x + с2y = d,
при некотором
значении d
= d1 достигнет
многоугольника D,
назовем эту точкуА«точкой
входа», и затем, пройдя многоугольник,
при некотором значении d
= d2 будем
иметь с ним последнюю общую точку В,
назовем В
«точкой
выхода». Очевидно, что своего наименьшего
и наибольшего значения целевая функция
F = с1x + с2y
достигнет
в точках «входа» А
и «выхода»
В.
Учитывая,
что оптимальное значение на множестве
допустимых решений целевая функция
принимает в вершинах области D,
можно предложить следующий алгоритм
решения задачи двумерного линейного
программирования графическим
методом.1)Строим
область допустимых решений функции
F.Для
этого в ограничениях знаки неравенства
заменяем знаками равенства и строим
полученные прямые. Затем определяем те
полуплоскости, которые соответствуют
данным ограничениям и получаем область
допустимых решений, лежащую на пересечении
всех полуплоскостей.»2)Строим
прямую уровня.Для
этого берём произвольную точку М,
принадлежащую области допустимых
решений функции F
и, подставив координаты этой точки в
функцию, получаем прямую уровня. Затем
от выбранной точки М, откладываем вектор
а, координаты которого – это коэффициенты
при целевой функции F.
3)Максимализируем
(минимизируем) целевую функцию F.
Для максимизации
(минимизации)функции F
передвигаем прямую уровня по направлению
(в обратном направлении относительно)
вектора а до пересечения с граничной
точкой области допустимых решений.
Полученная точка является оптимальным
решением, в котором функция достигает
свой максимум (минимум). Находим координаты
этой точки и представляем их в функцию
F.
Заметим, что вектор (с1, с2), перпендикулярный прямой, показывает направление роста целевой функции. При графическом решении ЗЛП возможны два случая, которые требуют особого обсуждения.
Случай 1. При перемещении прямой с1 x + с2y= d «вход» или «выход» (как на рисунке) произойдет по стороне многоугольника. Это случится, если в многоугольнике есть стороны, параллельные прямой с1х + с2у = d . В этом случае точек «выхода» («входа») бесчисленное множество, а именно – любая точка отрезка АВ. Это означает, что целевая функция принимает максимальное (минимальное) значение не в одной точке, а во всех точках, лежащих на соответствующей стороне многоугольника D.
Случай 2. Рассмотрим случай, когда область допустимых значений неограниченна. В случае неограниченной области целевая функция может быть задана таким образом, что соответствующая ей прямая не имеет точки «выхода» (или «входа»). Тогда максимальное значение функции (минимальное) не достигается никогда – говорят, что функция не ограничена.
Геометрическая интерпретация, которой мы пользовались при решении задач ЛП, перестает быть пригодной для этой цели при числе свободных переменных n – m > 3, а затруднительна уже при n – m = 3. Для нахождения решения задачи ЛП в общем случае применяются не геометрические, а вычислительные методы. Из них наиболее универсальным является так называемый симплекс-метод.
Универсальный
метод решения задач ЛП называется
симплекс-методом. Пример. Решить следующую
задачу ЛП в канонической форме
симплекс-методом.
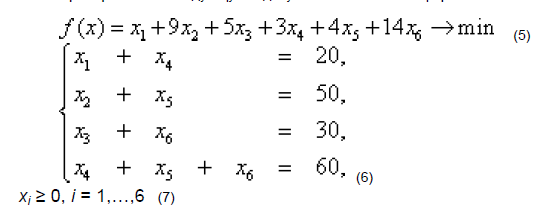
Говорят, что задача ЛП имеет каноническую форму, если все ограничения (кроме условий неотрицательности переменных) имеют вид равенств, а все свободные члены неотрицательны. Так что мы имеем задачу в канонической форме.
Идея симплекс-метода заключается в следующем. Сначала нужно найти некоторую (начальную) вершину многогранника допустимых решений (начальное допустимое базисное решение). Затем нужно проверить это решение на оптимальность. Если оно оптимально, то решение найдено; если нет, то перейти к другой вершине многогранника и вновь проверить на оптимальность. Ввиду конечности вершин многогранника (следствие конечности ограничений задачи ЛП) за конечное число "шагов" мы найдем искомую точку минимума или максимума. Надо заметить, что при переходе от одной вершины к другой значение целевой функции убывает (в задаче на минимум) или возрастает (в задаче на максимум).
Таким образом, идея симплекс-метода основывается на трех свойствах задачи ЛП.
ОДР не существует (ограничения противоречивы):
задача решений не имеет.
ОДР существует:
ОДР – замкнутый выпуклый N – угольник.
Задача имеет единственное решение, которое достигается в вершине ОДР.
Задача имеет множество решений, которые достигаютсяв любой точке, принадлежачей стороне ОДР.
ОДР – незамкнутый выпуклый N – угольник.
Задача имеет единственное решение, которое достигается в вершине ОДР.
Задача имеет множество решений, которые достигаютсяв любой точке, принадлежачей стороне ОДР.
Задача не имеет решений, так как ОДР неограничена в направлении возрастания (убывания) функции F.
