18. Графы типа дерево. Остовное дерево. Минимальное остовное дерево

Граф G называется деревом, если он является связным и не имеет циклов. Граф G, все компоненты связности которого являются деревьями, называется лесом.

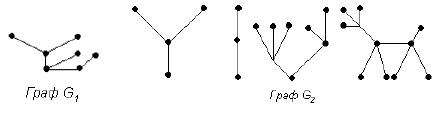
Граф G1 является деревом . Граф G2 является лесом , он содержит три связные компоненты, каждая из которых является деревом.

Следующие утверждения эквивалентны: граф G есть дерево; граф G является связным и не имеет простых циклов; граф G является связным и число его ребер ровно на единицу меньше числа вершин; любые две различные вершины графа G можно соединить единственной (и притом простой) цепью; граф G не содержит циклов, но, добавляя к нему любое новое ребро, получаем ровно один (с точностью до направления обхода и начальной вершины обхода) и притом простой цикл (проходящий через добавляемое ребро).

Если у дерева G есть, по крайней мере, одно ребро, то у него обязательно найдется висячая вершина. Пусть G – дерево. Тогда любая цепь в G будет простой.

Опр. Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.

Пусть G связный граф. Тогда остовное дерево графа G (если оно существует) должно содержать n(G) – 1 ребер. Таким образом, любое остовное дерево графа G есть результат удаления из G ровно m(G)-(n(G)-1)=m(G)-n(G)+1 ребер.

Опр. Число m(G)-n(G)+1 называется цикломатическим числом связного графа G и обозначается через v(G).

ЗАДАЧА О КРАТЧАЙШЕМ ПУТИ - Задача о нахождении на ориентированном графе пути наименьшей длины между двумя заданными его вершинами. Длиной пути такого графа называется сумма длин дуг, составляющих этот путь. Задача о кратчайшем пути возникает чаще всего при решении транспортных задач, дискретных задач динамического программирования и др.

Остовное дерево связного неориентированного графа — ациклический связный подграф данного графа, в который входят все его вершины. Иначе говоря, остовное дерево состоит из некоторого подмножества рѐбер графа, таких, что из любой вершины графа можно попасть в любую другую вершину, двигаясь по этим рѐбрами, и в нѐм нет циклов, то есть из любой вершины нельзя попасть в саму себя, не пройдя какое-то ребро дважды.

Понятие остовный лес неоднозначно, под ним могут понимать один из следующих подграфов:

любой ациклический подграф, в который входят все вершины графа, но не обязательно связный; в несвязном графе — подграф, состоящий из объединения остовных деревьев для каждой его компоненты связности.

Остовное дерево также иногда называют покрывающим деревом, остовом или скелетомграфа.

М инимальное остовное дерево (или минимальное покрывающее дерево) в связанном, взвешенном, неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рѐбер.

( Пример минимального остовного дерева в графе.Числа на ребрах обозначают вес ребер.)

Задача о нахождении минимального остовного дерева встречается в постановке: допустим, есть n городов, которые надо соединить дорогами, так, чтобы можно было добраться из любого города в любой другой (напрямую или через другие города). Разрешается строить дороги между заданными парами городов и известна стоимость строительства каждой дороги. Требуется решить, какие дороги нужно строить, чтобы минимизировать общую стоимость строительства.