Задача №6.02

Рассмотрим задачу №6.01. Пусть поставщик супа в пакетах предоставляет следующие скидки

Размер заказа	Цена, руб./шт.
1–199	2
200–499	1,96 (2% скидки)
500 и более	1,92 (4% скидки)

Следует ли владельцу магазина воспользоваться одной из скидок, предоставляемых поставщиком? Каковы при этом будут размер заказа и общие затраты на УЗ?

Решение

1. Строим пунктирными линиями графики трех функций затрат и обозначаем на них соответствующие цены 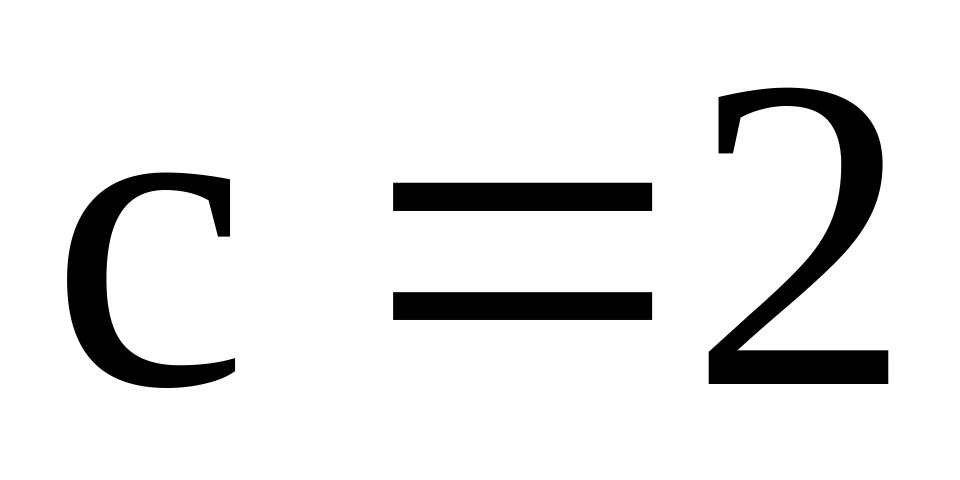, 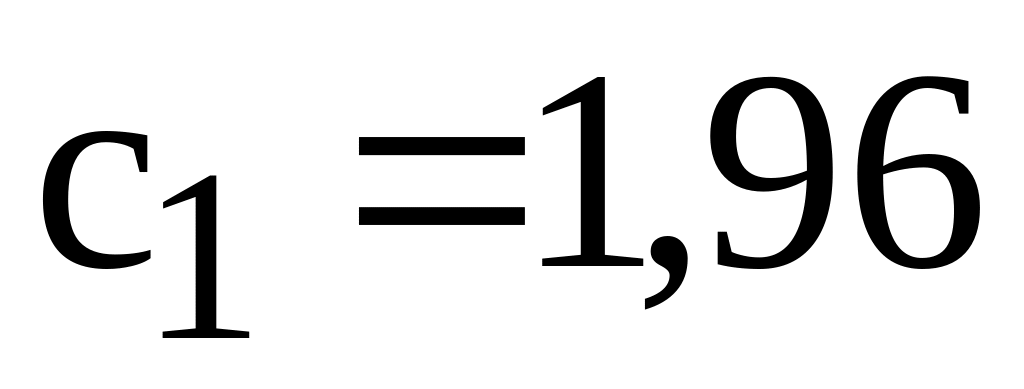и 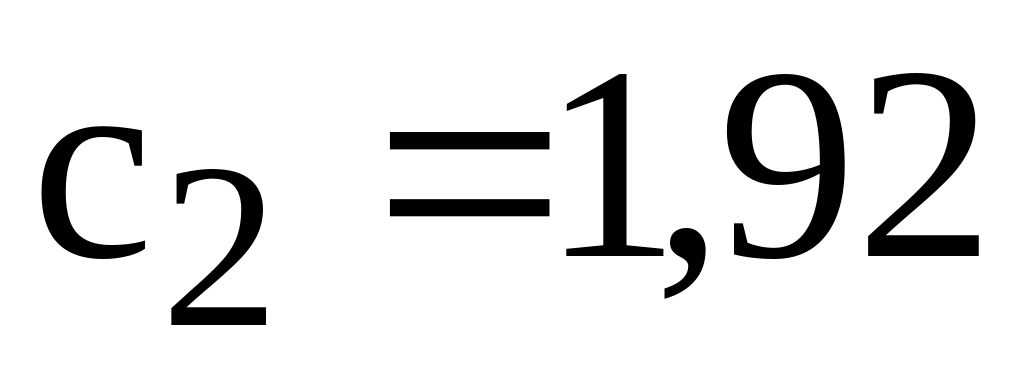(рис.6.6). Строим на графике точку, соответствующую .

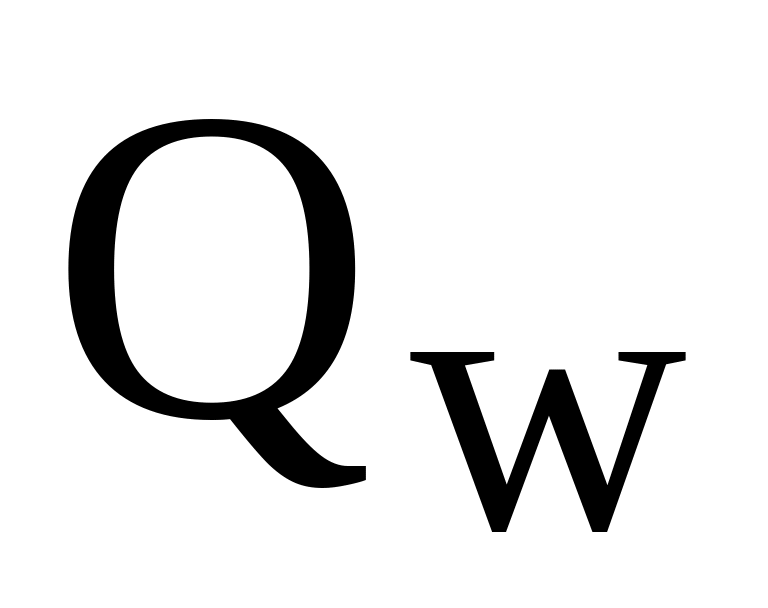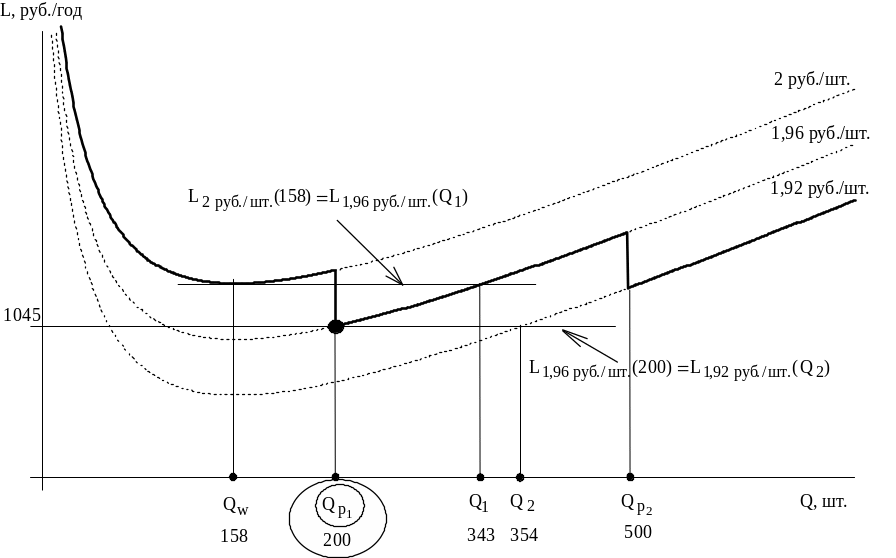
Рис.6.6. Решение задачи №6.02 с двумя скидками

2. Вычисляем значение =158 (см. решение задачи №5.01), отмечаем это значение на графике.

3. Поскольку 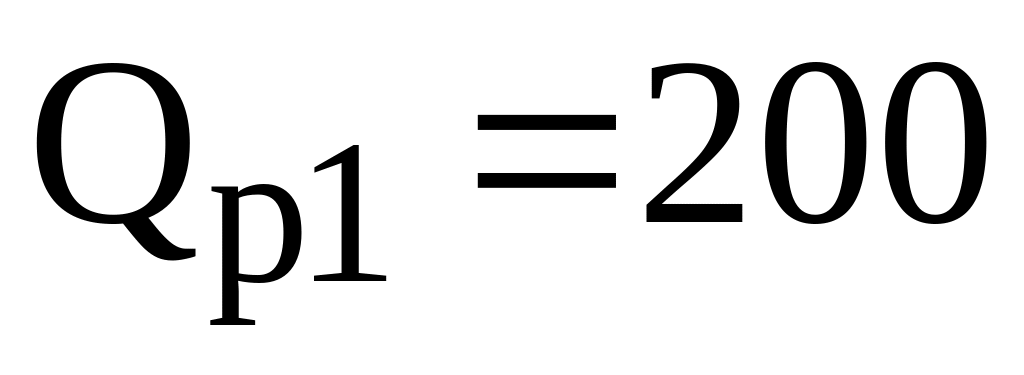не попадает в область I, то необходимо найти границу областей II и III. Для этого строим на графике уровень затрат, соответствующий заказу и цене с=2 руб. до пересечения со второй линией затрат, и графически находим и строим .

4. Находим численно, используя выражение

или ;

[шт.].

5. Используя правило (2) и график на рис.6.6, находим более дешевый объем заказа (с учетом только первой скидки)

[шт.].

5. Чтобы рассмотреть вторую скидку, построим на графике уровень затрат, соответствующий заказу, оптимальному при действии только первой скидки, т.е. и цене руб./шт. При пересечении этого уровня и третьей линии общих затрат графически определяем .

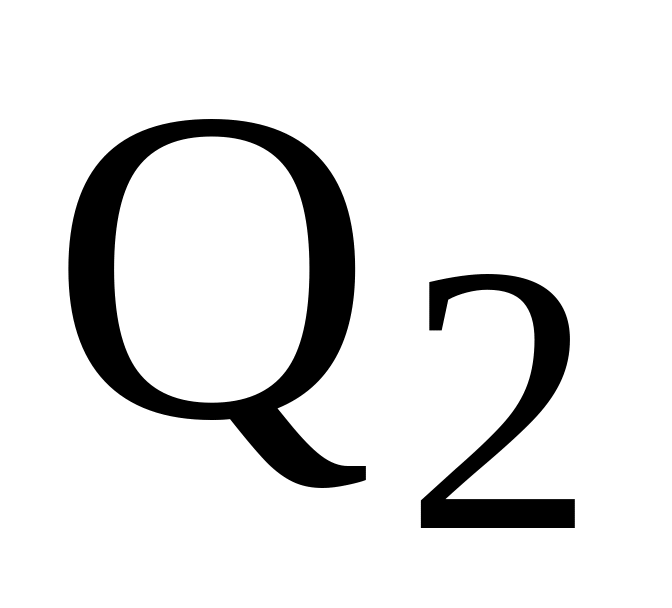6. Находим численно =354, исходя из выражения

или .

5. Используя правило (2) и график затрат, находим наиболее дешевый объем заказа с учетом первой и второй скидок

шт.

Таким образом, пользоваться второй скидкой владельцу магазина невыгодно. Оптимальный для него вариант – заказывать 200 пакетов по цене 1,96 руб./шт. обойдется в [руб./год].

Методические рекомендации и задания к контрольной работе

Домашняя контрольная работа - решение задач лабораторных работ, согласно условиям своего варианта.

ЛАБОРАТОРНАЯ РАБОТА №1 (ЧАСТЬ I)

“ОДНОИНДЕКСНЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ”

1.1. Цель работы

Приобретение навыков построения математических моделей одноиндексных задач ЛП и решения их в Microsoft Excel.

1.2. Порядок выполнения работы

1. Согласно номеру своего варианта выберите условие задачи и постройте ее модель.

2. Найдите оптимальное решение задачи в Excel и продемонстрируйте его преподавателю.

Примечание 1.1. Расчет числовых данных, которые непосредственно не заданы в условии задачи, производите непосредственно в ячейках экранной формы. Например, для ввода коэффициента при в левой части (2.3) в соответствующую ячейку надо ввести выражение =4/60, после чего в ячейке отобразится результат вычисления, то есть 0,066666667. Для ввода правой части ограничения (2.3) в соответствующую ячейку надо ввести выражение =14*8*1*22, при этом в ячейке отобразится число 2464. Этот способ позволяет четко представлять путь получения числовых данных в ячейках экранной формы, избегать ошибок при расчете параметров задачи, а также обеспечивает высокую точность расчетов.

3. Оформите отчет по лабораторной работе, который должен содержать:

исходные данные варианта;

построенную модель задачи с указанием всех единиц измерения;

результаты решения задачи.