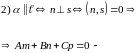- •1 Билет.
- •2 Билет.
- •3 Билет.
- •4 Билет.
- •5 Билет.
- •6 Билет.
- •7 Билет.
- •8 Билет.
- •9 Билет.
- •10 Билет.
- •11 Билет.
- •1 Билет.
- •2 Билет.
- •3 Билет.-
- •4 Билет.-
- •5 Билет.
- •6 Билет.-
- •7 Билет.
- •8 Билет.
- •9 Билет.
- •10 Билет.
- •5 Билет.
- •6 Билет.
- •7 Билет.
- •8 Билет.
- •9 Билет.
- •10 Билет. Угол между прямыми в пространстве
- •Угол между прямой и плоскостью
- •3 Билет.
- •4 Билет.
- •5 Билет.
- •6 Билет.-
- •7 Билет.
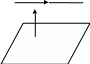
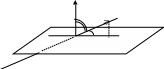
Угол между прямой и плоскостью
ОПРЕДЕЛЕНИЕ. Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость.
Пусть в некоторой пдск заданы плоскость
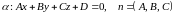
и прямая
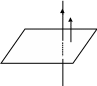
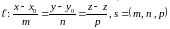 (рис. 50).
(рис. 50).
Рис. 50 |
|
Рис. 51
|
1)
условие перпендикулярности прямой и плоскости (рис. 51).
|
Рис. 52 |
– условие параллельности прямой и плоскости (рис. 52).
|
11 билет.-
12 билет.-
13 билет.-
Матан.
1 билет.
Чтобы задать функцию, надо
1) задать множество Х,
2) определить
правило установления соответствия
между
 и
и
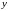 .
.
Способы задания функции:
1) аналитический (с помощью формул)
ПРИМЕР.
а)
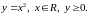 б)
б)

в)
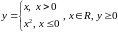 .
.
2) табличный
ПРИМЕРОМ табличного задания функции является расписание.
3) графический.
2 билет.
Если каждому
значению
из натурального ряда чисел 1,2,3,…,
,…ставится
в соответствие по некоторому правилу
действительное число
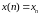 ,
то множество занумерованных действительных
чисел
,
то множество занумерованных действительных
чисел
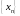 называется числовой последовательностью.
называется числовой последовательностью.
Таким образом, последовательность – функция натурального аргумента,
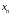 называется общим
или
-м
членом последовательности. Зная общий
член
,
можно найти любой член последовательности.
называется общим
или
-м
членом последовательности. Зная общий
член
,
можно найти любой член последовательности.
ПРИМЕР.
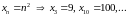
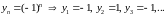
3 Билет.
ОПРЕДЕЛЕНИЕ. Если каждому значению из натурального ряда чисел 1,2,3,…, ,…ставится в соответствие по некоторому правилу действительное число , то множество занумерованных действительных чисел называется числовой последовательностью.
Таким образом, последовательность – функция натурального аргумента,
называется общим или -м членом последовательности. Зная общий член , можно найти любой член последовательности.
ПРИМЕР.
ОПРЕДЕЛЕНИЕ.
Последовательность
называется ограниченной сверху (снизу),
если
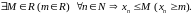 называется верхней гранью, а
нижней гранью последовательности.
называется верхней гранью, а
нижней гранью последовательности.
ПРИМЕРЫ.
а)
=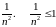 или
или
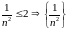 ограничена сверху:
ограничена сверху:
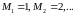
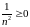 или
или
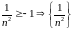 ограничена снизу:
ограничена снизу:
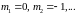
б)
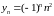 – сверху неограничена и снизу неограничена.
– сверху неограничена и снизу неограничена.
в)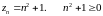 или
или
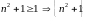 ограничена снизу:
ограничена снизу:
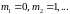 Сверху
Сверху
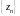 неограничена.
неограничена.
Если последовательность имеет верхнюю или нижнюю грани, то они неединственны.
ОПРЕДЕЛЕНИЕ.
Последовательность
называется ограниченной, если она
ограничена сверху и снизу, то есть
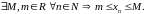
ПРИМЕР.
ограничена, так как
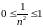 или
или
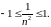
Сформулируем еще одно эквивалентное этому определение ограниченной последовательности, которым, как правило, более удобно пользоваться.
ОПРЕДЕЛЕНИЕ.
Последовательность
называется ограниченной, если
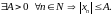
ОПРЕДЕЛЕНИЕ.
называется неограниченной, если для
любого положительного
найдется хотя бы один элемент
такой, что
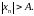
ОПРЕДЕЛЕНИЕ.
называется бесконечно большой, если
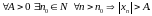
ПРИМЕРЫ.
а)
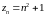 :
2,5,10,17,26,…1001,… – неограниченная и
бесконечно большая.
:
2,5,10,17,26,…1001,… – неограниченная и
бесконечно большая.
б)
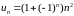 :
0,8,0,32,0,72,… – неограниченная, но не
бесконечно большая.
:
0,8,0,32,0,72,… – неограниченная, но не
бесконечно большая.
Всякая бесконечно большая последовательность неограничена. Обратное утверждение неверно.
ОПРЕДЕЛЕНИЕ.
Последовательность
 называется бесконечно малой (б.м.), если
называется бесконечно малой (б.м.), если
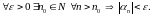
ПРИМЕР.
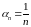 .
Если
.
Если
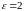 ,
то
,
то
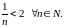
Если
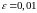 ,
то
,
то
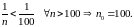
Если
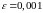 ,
то
,
то
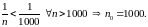
Пусть
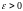 произвольно, тогда
произвольно, тогда
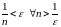 .
Таким образом,
бесконечно мала.
.
Таким образом,
бесконечно мала.

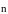
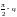
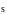
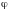
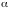
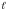
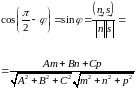
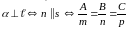 –
–