5 Билет.

Кривые второго порядка – плоские линии, которые в пдск задаются уравнениями второй степени относительно двух переменных

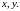
6 Билет.

Окружностью называется совокупность точек плоскости, равноудаленных от фиксированной точки, называемой ее центром.

Эллипс – совокупность точек плоскости, сумма расстояний от которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.

Гипербола – совокупность точек плоскости, модуль разности расстояний от которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная, не равная нулю и меньшая, чем расстояние между фокусами.

Парабола – совокупность точек плоскости, равноудаленных от фиксированной точки этой плоскости, называемой фокусом, и фиксированной прямой, не проходящей через эту точку, называемой директрисой.

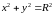. (3.10)

(3.10) – каноническое уравнение окружности.

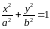(3.14)

(3.14) – каноническое уравнение эллипса.

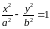, (3.18)

(3.18) – каноническое уравнение гиперболы.

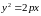, (3.22)

(3.22) – каноническое уравнение параболы; называется ее параметром.

Если фокус параболы на оси ОУ (рис. 35), то ее каноническое уравнение имеет вид .

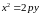7 Билет.

Любой ненулевой вектор , перпендикулярный плоскости 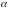, называется ее нормальным вектором, или нормалью. ( не полностью нашла )

8 Билет.

Углом между плоскостями называется любой из двух смежных двугранных углов, образованных плоскостями при их пересечении. Если плоскости параллельны, то угол между ними равен или 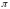радиан.

Рассмотрим плоскост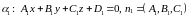и и

.

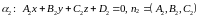Очевидно,

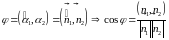
или .

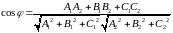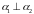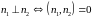Если , то – условие перпендикулярности плоскостей.

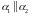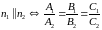Если , то – условие параллельности плоскостей.

ПРИМЕР. Найти угол между плоскостями

.

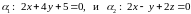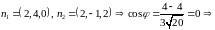плоскости перпендикулярны.

9 Билет.

Если 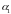не параллельна 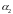, то есть 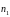не коллинеарен 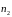, то система уравнений

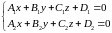
определяет прямую линию в пространстве.

10 Билет. Угол между прямыми в пространстве

Рассмотрим прямые, заданные в некоторой пдск каноническими уравнениями:

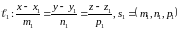
и

.

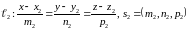ОПРЕДЕЛЕНИЕ. Углом между прямыми в пространстве называется угол между двумя пересекающимися прямыми, проходящими через произвольную точку пространства параллельно данным.

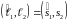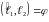Из определения следует, что . Если , то

.

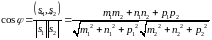1) 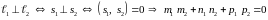– условие перпендикулярности прямых.

2) 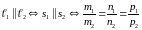– условие параллельности прямых в пространстве.

ПРИМЕР. Найти угол между прямой 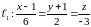и прямой , проходящей через точк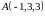и и .

.

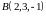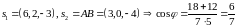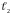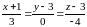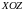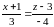Заметим, что уравнение прямой имеет вид: . В данном случае ноль в знаменателе писать принято: он означает, что направляющий вектор прямой (и сама прямая) параллелен плоскости . Эта прямая является результатом пересечения плоскостей и .
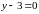