7 Билет.

1 вопрос. Матрица 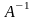называется обратной для матрицы , если она вместе с удовлетворяет условию: 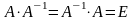, где – единичная матрица.

Из определения следует, что и – перестановочные, значит, обратная матрица существует лишь для квадратной матрицы (прямоугольные матрицы обратных не имеют).

2 ВОПРОС –

8 Билет.

Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если решений у нее более одного.

ПРИМЕР.

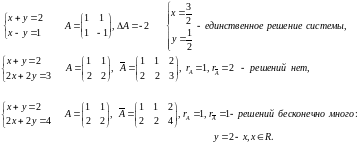
9 Билет.

ТЕОРЕМА. (Кронекера-Капелли, критерий совместности системы линейных уравнений) Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг ее основной матрицы был равен рангу расширенной (без доказательства).

СЛЕДСТВИЕ. Для того чтобы однородная система 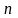уравнений с неизвестными имела ненулевое решение, необходимо и достаточно, чтобы ее основной определитель был равен нулю.

ДОКАЗАТЕЛЬСТВО.

1) Достаточность: система имеет нетривиальное решение.

Так как единственный минор -го порядка равен нулю, то , значит, нетривиальное решение существует.

2) Необходимость: система имеет нетривиальное решение .

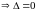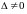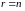Если , то не равен нулю минор -го порядка основной матрицы, значит, и решение единственно, что противоречит условию

10 Билет.

1 ВОПРОС. ТЕОРЕМА. Для того чтобы система линейных однородных уравнений (1.15) имела нетривиальное решение, необходимо и достаточно, чтобы ранг ее основной матрицы 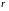был меньше числа неизвестных .

ДОКАЗАТЕЛЬСТВО.

1) Достаточность: 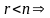(1.15) имеет нетривиальное решение.

По теореме о числе решений система в этом случае имеет бесконечное множество решений, среди которых содержатся и нетривиальные.

2) Необходимость: (1.15) имеет нетривиальное решение .

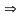Пусть , тогда по теореме о числе решений система (1.15) имеет единственное решение. Это решение тривиальное, что противоречит условию. Поэтому сделанное предположение неверно и .

ИЛИ

СЛЕДСТВИЕ. Для того чтобы однородная система уравнений с неизвестными имела ненулевое решение, необходимо и достаточно, чтобы ее основной определитель был равен нулю.

ДОКАЗАТЕЛЬСТВО.

1) Достаточность: система имеет нетривиальное решение.

Так как единственный минор -го порядка равен нулю, то , значит, нетривиальное решение существует.

2) Необходимость: система имеет нетривиальное решение .

Если , то не равен нулю минор -го порядка основной матрицы, значит, и решение единственно, что противоречит условию.

11 Билет.

ПРИМЕР. Решить систему уравнений матричным способом:

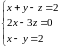
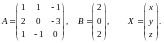
В предыдущем примере было показано, что 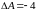, значит, систему матричным способом решить можно. Там же была найдена обратная матрица

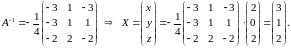
Таким образом, 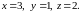Проверкой убеждаемся, что решение найдено верно.

Вернемся к равенству (1.12). Из него следует, что

,

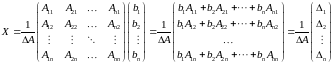поэтому 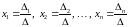, (1.13)

где 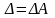, 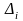– определитель матрицы, полученной из А заменой ее -го столбца на столбец правых частей системы (1.10) , = 1,2,…,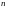 . Формулы (1.13) называются формулами Крамера.

ПРИМЕР. Решить систему линейных уравнений: .

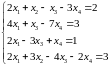Выпишем расширенную матрицу и системы и упростим ее с помощью элементарных преобразований над строками:

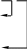
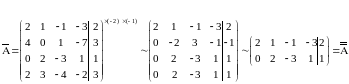
Очевидно, что 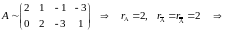по теореме

Кронекера-Капелли система совместна.

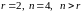, значит, по теореме о числе решений система неопределенная, то есть имеет бесконечное множество решений и 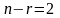– число свободных переменных.

Выпишем систему, соответствующую матрице и эквивалентную исходной:

.

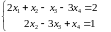Перенесем в правую часть переменные 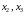, считая их свободными (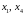 – зависимые переменные):

.

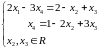Теперь подставим 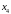в первое уравнение и выразим 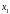через свободные переменные:

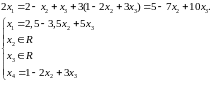– общее решение системы.

Векторная алгебра.