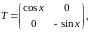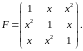1 Билет.
1 ВОПРОС. Числовой
матрицей
размера m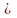
n
называется совокупность
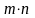чисел, расположенных в виде таблицы,
содержащей m
строк и n
столбцов.
2 ВОПРОС. Правила линейных операций:
1.Пусть
=
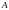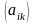и
=
,
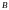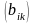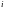=1,2,…,
,
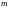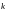=1,2,…,
– матрицы размера
.
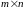Матрица
=
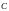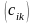также размера
называется суммой
матриц
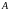и
,
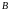если
,
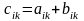=1,2,…,
,
=1,2,…,
ПРИМЕР.
=
,
=
=
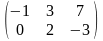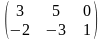
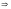
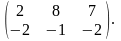
2.
Произведением
матрицы
=
размера
на число
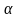называется матрица
=
того же размера, элементы которой
,
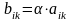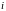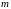=1,2,…,
,
k=1,2,…,
.
ПРИМЕР.
=
=
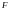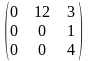
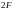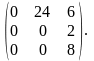
3.
Нулевой
матрицей
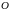называется матрица, все элементы которой
равны нулю.
4.
Матрица
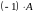называется противоположной
для
и обозначается
.
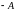Очевидно, что
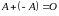для любой матрицы А.
5.
Разностью
матриц
и
одного размера называется сумма
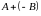и обозначается
.
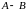6. Результат конечного числа линейных операций над матрицами называется их линейной комбинацией.
ПРИМЕР.
Пусть
=
,
=
.
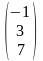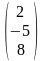Матрица
=
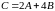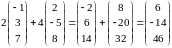– линейная
комбинация матриц и с коэффициентами 2 и 4.
Транспонированной
матрицей
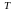для матрицы
размера
называется матрица размера
,
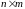полученная из
заменой всех ее строк столбцами с теми
же порядковыми номерами.
То есть, если
=
,
то
,
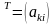=1,2,…,
,
=1,2,…,
.
ПРИМЕР.
=
;
=
=
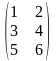
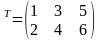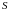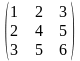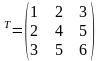
3х2 2х3 3х3 3х3
Пусть
=
– матрица размера
,
=
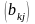– матрица размера
.
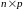Произведение этих матриц
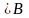– матрица
=
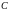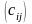размера
,
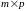элементы которой вычисляются по формуле:
,
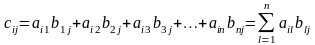=1,2,…,
,
=1,2,…,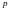
,
то есть элемент
-й
строки и
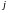-го
столбца матрицы
равен сумме произведений соответствующих
элементов
-й
строки матрицы
и
-го
столбца матрицы
.
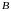ПРИМЕР.
=
,
=
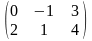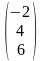
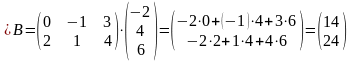
2х3 3х1 2х3 3х1 2х1
Произведение
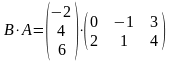– не существует.
3х1 2х3
2 Билет.
1 ВОПРОС.
,
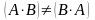даже если оба произведения определены.
ПРИМЕР.
,
,
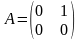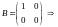
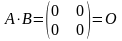хотя
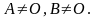
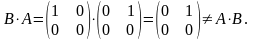
2 ВОПРОС. Матрицы
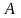и
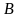называются перестановочными,
если
,
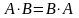в противном случае
и
называются неперестановочными.
Из определения следует, что перестановочными могут быть лишь квадратные матрицы одного размера.
ПРИМЕР.
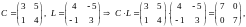
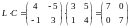матрицы
и
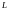перестановочные.
,
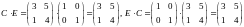то есть
,
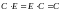значит,
и
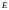– перестановочные матрицы.
Вообще единичная
матрица перестановочна с любой квадратной
матрицей того же порядка, и для любой
матрицы
.
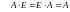Это свойство матрицы
объясняет, почему именно она называется
единичной: при умножении чисел таким
свойством обладает число 1.
Если соответствующие произведения определены, то:
2.
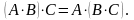
3.
,
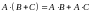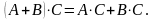
4.
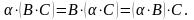
5.
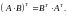
ПРИМЕР.
,
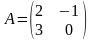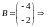
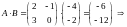
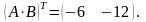
2х2 2х1 2х1 1х2
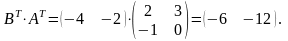
1х2 2х2 1х2
ЗАМЕЧАНИЕ. Элементами матрицы могут быть не только числа, но и функции. Такая матрица называется функциональной.
ПРИМЕР.
