11. Собственные значения матрицы. Собственные и присоединённые векторы матрицы.

Пусть А- квадратная матрица порядка n

Определение 1. Комплексное число называется собственным значением матрицы А, если существует ненулевое решение матричного уравнения

Алгебраическая кратность собственного значения лямбда матрицы А, называеться кратность коря лимба характеристического уравнением Det(A-גE)

Квадратная матрица порядка n имеет с учетом кратности M собственных значений

Собственный вектор квадратной матрица А называеться отвечающий её собственному значению лямбда, называеться не нулевое решение Ах=גх

Собственные вектора квадратной матрицы отвечающие различным её собственным значениям называемых линейным

Каждому собственному значению лямбда матрицы а отвечает m=n-rang(A-גE) линейно не зависимых собственных векторов

Геометрическая кратность собственного значения лямбда квадратной матрицы А называется количество линейно не зависимых собственных векторов этой матрицы отвечают их собственному значению Лямбда

12. Комплексные числа, их геометрическая интерпретация.

Определение. Комплексным числом z называется выражение , где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:

Определение. Числа и 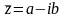называются комплексно – сопряженными.

Определение. Два комплексных числа 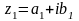и называются равными, если соответственно равны их действительные и мнимые части:

Определение. Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части.

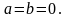
1) два комплексных числа z₁ = (x₁, y₁) и z₂ = (x₂, y₂) называются равными, если x₁ = x₂ и y₁ = y₂;

2) суммой комплексных чисел z₁ и z₂ называется комплексное число z вида z = (x₁ + x₂, y₁ + y₂);

3) произведением комплексных чисел z₁ и z₂ называется комплексное число

z = (x₁x₂ - y₁y₂, x₁y₂ + x₂y₁);

4) множество комплексных чисел , отождествляется с множеством действительных чисел R.

Разностью комплексных чисел z₁ и z₂ называется комплексное число z такое, что z₂ + z = z₁, откуда находим z = z₁ - z₂ = (x₁ - x₂, y₁ - y₂).

Частным комплексных чисел z1 и z2 называется комплексное число z такое, что . Отсюда находим Z=( ; )

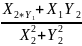13. Алгебраическая форма комплексного числа. Действия над комплексными числами.

Z=x+yi алгебраическая форма

Z=x-jy число сопряженное числу Z=x+yi

j - мнимая единица

j²=-1

1)Сложение и вычитание.

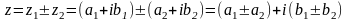
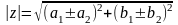
3. Умножение.

В тригонометрической форме:

,

3) Деление.

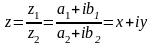
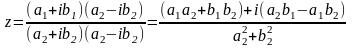
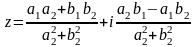
В тригонометрической форме:

4) Возведение в степень.

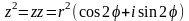
В общем случае получим: ,

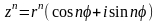5) Извлечение корня из комплексного числа.

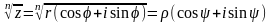
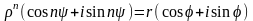
Отсюда:

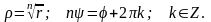
14. Модуль и аргумент комплексного числа. Главное значение аргумента. Тригонометрическая и показательная формы комплексного числа. Действия над комплексными числами в тригонометрической форме.

Z=a+b A=(a,b)

|Z|=r=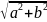

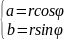
Z=r(cos +sin )

ArgZ=h –аргумент комплексного числа

-

|Z|=

=cos +sin формула Эйлера

z показатель формулы комплексного числа

тригонометрической формой комплексного числа.

Пример:

Z=4+3i

X=4 y=3 >0. 2 четверть

|Z|=sqrt(4*4+3*3)=sqrt25=5

Tga=y/x=3/4

a=arctg(3/4)+ПК

argZ=arctg(3/4)

Z=5*(cos(arctg(3/4))+isin(arctg(3/4))) –тригонометрическая форма.

Z=5*e*arctg(3/4) – показательная форма.

Действия

1) Умножение

2) Деление

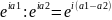
3)Введение в степень 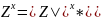+isin(xa))

- формула Муавра

4) извлечение корня из n степени