6. Определитель квадратной матрицы. Вычисление определителей второго и третьего порядков.

Определителем квадратной матрицы А порядка n называется алгебраическая сумма n! произведения вида (-1)^n(a) a1j₁ a2j_{2 …}anj_{n ­} в каждом из которых содержится по 1 – ому элементу из каждой строки и каждого столбца.

1. Вычисление по любой строке и любому столбцу

2. Вычисление треугольником

3. Правилом дополнения

7. Свойства определителей.

1. Если все элементы некоторой строки или столбца равны 0, то определитель равен 0

2. Если определитель имеет 2 одинаковых строки или 2 одинаковых столбца, то он равен 0

3. Если элементы 2 строк пропорциональны то определитель равен 0

4. (Линейная зависимость строк и столбцов)

Если все элементы К ого столбца определителя N порядка имеют вид

Aij=L1*ai1+L2*ai2+…+Lk1*aik+Lk+1*aik+…+Ln*ain то определитель равен 0

Замечание: имеет место аналогичное свойство для строк

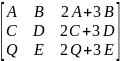=0

5. При транспортировании матриц определитель не меняется

6. Общий множитель некоторой строки элементов выноситься за знак определителя

7. При перестановке 2 ух строк или 2 ух столбцов определителя изменяется только знак

8. Если в некоторой строке прибавить другую строку умноженную на произвольные числа то определитель не измениться

9. Если к некоторому столбцу прибавить другой столбец умноженный на любое число то определитель не изменится

10. Если все элементы К ого столбца определителя Д n-ого порядка приставить в виде

Aij=L₁Bi1+L₂bi2 , то Д=L₁Д₁+L₂Д₂

11. Определитель Д ого порядка равен сумме по парных произведений всех элементов I ой строки, на их алгебраические дополнения

12. Определитель треугольной и диагональной матрицы равен произведению всех её элементов главной диагонали

13. det A = det A^T;

14. det ( A  B) = det A  det B.

15. det (AB) = detAdetB

8. Общие способы вычисления определителей.

1. Приведение к треугольному виду; свойства 6 и 8

2. Разложение определителя по строке; свойство 10

3. Разложение определителя по столбцу; свойство 11

4. Представление определителя в виде суммы определителей

5. Метод рекурертных соотношений

6. Теорема Лапаса

9. Ранг матрицы, его свойства. Методы нахождения ранга матрицы.

Определение. Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s.

Определение. Порядок базисного минора матрицы называется рангом матрицы и обозначается

Rang А.

Теорема. Наибольшее число линейно независимых столбцов в матрице равно числу линейно независимых строк.

Методы нахождения ранга матрицы

1. нахождение ненулевых строк.

2. По нахождению базисного минора.

10. Обратная матрица. Теорема о существовании обратной матрицы. Методы нахождения обратной матрицы.

Определим операцию деления матриц как операцию, обратную умножению.

Определение. Если существуют квадратные матрицы Х и А, удовлетворяющие условию:

XA = AX = E,

где Е - единичная матрица того же самого порядка, то матрица Х называется обратной к матрице А и обозначается А^-1.

Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.

Рассмотрим общий подход к нахождению обратной матрицы.

Исходя из определения произведения матриц, можно записать:

AX = E  , i=(1,n), j=(1,n),

Пример. Дана матрица А = , найти А^-1.

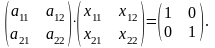
Таким образом, А^-1= .

Для нахождения обратных матриц больших порядков, применяют следующую формулу:

где М_ji- дополнительный минор элемента а_ji матрицы А.

Пример. Дана матрица А = , найти А^-1. det A = 4 - 6 = -2.

M₁₁=4; M₁₂= 3; M₂₁= 2; M₂₂=1

x₁₁= -2; x₁₂= 1; x₂₁= 3/2; x₂₂= -1/2

Таким образом, А^-1= .

свойства

1) (A^-1)^-1 = A;

2) (AB)^-1 = B^-1A^-1

3) (A^T)^-1 = (A^-1)^T.