
- •Производная функции. Дифференцирование суммы, разности, произведения и частного двух функций. Геометрический смысл производной функции.
- •Дифференциал функции, его свойства.
- •Дифференцирование элементарных функций. Табличные производные.
- •Понятие матрицы. Операции над матрицами, их свойства.
- •Квадратная матрица. Треугольная, диагональная, единичная матрицы. Степень квадратной матрицы. Матричный многочлен.
- •Определитель квадратной матрицы. Вычисление определителей второго и третьего порядков.
- •Свойства определителей.
- •Общие способы вычисления определителей.
- •Ранг матрицы, его свойства. Методы нахождения ранга матрицы.
- •Обратная матрица. Теорема о существовании обратной матрицы. Методы нахождения обратной матрицы.
- •Собственные значения матрицы. Собственные и присоединённые векторы матрицы.
- •Комплексные числа, их геометрическая интерпретация.
- •Корень n-ой степени из комплексного числа. Логарифм и степень комплексного числа.
- •Правило Крамера. Решение линейных систем алгебраических уравнений.
- •Системы линейных алгебраических уравнений. Общие понятия. Теорема Кронекера-Капелли.
- •Однородные и неоднородные системы линейных алгебраических уравнений. Теоремы о существовании решений. Структура общего решения.
- •Системы координат на плоскости.
- •Прямая на плоскости. Различные уравнения прямой на плоскости
- •Условия пересечения, параллельности, совпадения и перпендикулярности двух прямых на плоскости. Определение угла между двумя прямыми.
- •Уравнение кривой на плоскости. Кривые второго порядка на плоскости, их классификация. Кривая второго порядка может быть задана уравнением
- •Эллипс, его свойства и изображение.
- •Гипербола, её свойства и изображение.
- •Парабола, её свойства и изображение.
- •Системы координат в пространстве.
- •Уравнения плоскости в пространстве. Условия пересечения, параллельности, совпадения и перпендикулярности двух плоскостей в пространстве. Определение угла между двумя плоскостями.
- •Уравнения прямой в пространстве. Условия пересечения, параллельности, совпадения и перпендикулярности двух прямых в пространстве. Определение угла между двумя прямыми.
- •Поверхности второго порядка, их классификация и изображения
Производная функции. Дифференцирование суммы, разности, произведения и частного двух функций. Геометрический смысл производной функции.
Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.
Производная - основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.
Дифференцирования
суммы:
![]()
Дифференцирования разности:
Дифференцирования
произведения
(правило Лейбница):
![]()
Дифференцирования частного:


 у
у
f(x)
f(x0 +x) P
f
f(x0) M
x
0 x0 x0 + x x
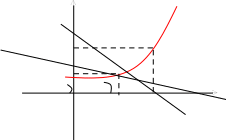
Пусть f(x)
определена на некотором промежутке (a,
b). Тогда
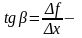 тангенс угла наклона секущей МР к графику
функции.
тангенс угла наклона секущей МР к графику
функции. ,
,
где - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.
Уравнение касательной к кривой:
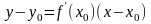
Уравнение нормали
к кривой:
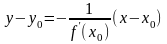 .
.
Производные основных элементарных функций.
1)С = 0; 9)

2)(xm)
= mxm-1;
10)
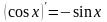
3)
 11)
11)

4)
 12)
12)

5)
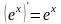 13)
13)

6)
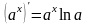 14)
14)

7)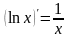 15)
15)
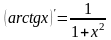
8)
 16)
16)
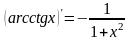
Дифференциал функции, его свойства.
Определение. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции.
Обозначается dy или df(x).
Из определения следует, что dy = f(x)x или
dy = f(x)dx.
Можно также записать:

Дифференциал функции f – это линейная функция y=f’(x0)*(x-x0) в точке x0 и обозначают df. Для функции x производная в каждой точке равна 1, то есть dx=x-x0 Поэтому пишут: df=f’(x)dx
Дифференциал в математике — линейная часть приращения функции или отображения.
Приближенное значение функции вблизи точки равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом: f’(x)=df/dx
Геометрически дифференциал функции df – это приращение ординаты касательной к графику функции в данной точке при изменении абсциссы точки на dx.
Свойства
1) d(u ± v) = (u ± v)dx = udx ± vdx = du ± dv
2) d(uv) = (uv)dx = (uv + vu)dx = vdu + udv
3) d(Cu) = Cdu
4)
![]()
Дифференцирование элементарных функций. Табличные производные.
Дифференцирование элементарных функций
(X+Y) ’=X’+Y’
(X-Y) ’=X’-Y’
(C*X) ’=C*X’, Где С это постоянная
(X*Y) ’=X’Y+XY’
(X/Y) ’=( X’Y-XY’)/(Y*2)
(F(K*X+B)) ’=KF’*(KX+B) ’
(F(g(X)) ’=F’(g(X))*g’ (x)
Табличные производные
C’=0, где С постоянная
(Xn) ’=n*xn-1
 =
=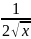
(ex)’=ex
(Ax)’=Ax*ln g
(Ln x)’=

(sin x)’= cos x
(Cos x)’= - sin x
(Tg x)’=

(Ctg x)’ = -

(Arcsin x) ’=
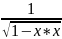
(Arcos x) ’= -
(Arctg x) ’=
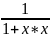
14) (Arcctg x) ’= -
