1.Метрология – наука об измерениях методах и средствах обеспечения их единства и способах достижения требуемой точности.Предметом заканадательной метрологии яявляется устоновление обязательныъ технических и юридических требований по приминению единиц физических величин эталонов методов и средств измерений направленных на обеспечение единсвта и необходимости точности измерений.Физическая велечина – свойство общее в качественном отношении для множества обектов физических систем их состояний и происходивших в них процессов.это свойствао является индивидуальным в количественном отношении для каждого из обектов.значение физ.велечины оно отражает в качественном и кол-венном отношениях соотвествующее свойство обекта. - Единица физической величины - физическая величина (ФВ) фиксированного размера, которой условно присвоено значение, равное единице, и применяемая для количественного выражения однородных физических величин. Прямое измерение – измерение, при котором искомое значение величины находят непосредственно из опытных данных.

Косвенное измерение – измерение, при котором искомое значение величины находят по известной зависимости межу этой величиной и величинами, подвергаемыми прямым измерениям (нахождение плотности по массе и размерам)

Совокупные измерения – производимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин находят из системы уравнений, получаемых при прямых измерениях (нахождение массы гири в наборе по известной массе одной из них и по результатам сравнения масс различных сочетаний гирь)

Совместные измерения – проводимые одновременно измерения двух или более неодноименных величин для выявления зависимости между ними.

Абсолютными называют измерения, которые основаны на прямых измерениях одной или нескольких основных величин или на использовании значений физических констант.

Относительными называют измерения, при которых искомую величину сравнивают с одноименной величиной, играющей роль единицы или принятой за исходную.

3. Под абсолютной погрешностью измерения понимают разность между полученным в ходе измерения и истинным значением физической величины:

Относительная погрешность представляет собой отно­шение абсолютной погрешности к истинному значению измеряемой величины:

Систематическая погрешность — погрешность, изменяющаяся во времени по определённому закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т. п.), неучтёнными экспериментатором.

Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора или если произошло замыкание в электрической цепи).

Случайная погрешность — составляющая погрешности измерения, изменяющаяся случайным образом в серии повторных измерений одной и той же величины, проведенных в одних и тех же условиях.

ПОГРЕШНОСТЬ МЕТОДА ИЗМЕРЕНИЙ - (погрешность метода) [error of method] - составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений.

Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.

5. Количественной характеристикой измеряемой величины служит ее размер. Получение информации о размере физической или нефизической величины является содержанием любого измерения.

Формализованным отражением качественного различия измеряемых величин является их размерность. Согласно международному стандарту ИСО размерность обозначается символом dim. Размерность основных величин — длины, массы и времени — обозначается соответствующими заглавными буквами: dim l = L; dim m = М; dim t = Т.

В физике и технике единицы измерения (единицы физических величин, единицы величин^[1]) используются для стандартизованного представления результатов измерений. Использование термина единица измерения противоречит рекомендациям метрологических изданий^[2], однако он широко употребляется в научной литературе^[3]. Численное значение физической величины представляется как отношение измеренного значения к некоторому стандартному значению, которое и является единицей измерения. Число с указанием единицы измерения называется именованным.

Различают основные единицы измерения, которые определяются с помощью эталонов, и производные единицы, определяемые через основные. Выбор величины и количества основных единиц измерения может быть произвольным и определяется только традициями или соглашениями. Существует большое количество различных систем единиц, которые различаются выбором основных единиц измерения.

Государство, как правило, законодательно устанавливает какую-либо систему единиц. Метрология непрерывно работает над улучшением единиц измерения и основных единиц и эталонов.

7. СИТУАЦИОННОЕ МОДЕЛИРОВАНИЕ (от франц. situation — положение, обстановка, стечение обстоятельств...) — разновидность физического моделирования, воспроизводящего сравнительно небольшое количество факторов деятельности, необходимых и достаточных для адекватного воспроизведения конкретной ситуации управления объектом в СЧМ

Информация - это совокупность сведений, уменьшающих начальную неопределенность знаний об объекте. ^ Измерительная информация - информация о значениях измеряемой физической величины.

9. Необходимым условием проведения однократного измерения служит наличие априорной информации. К ней относится, например, информация о виде закона распределения вероятности показания и мере ее рассеяния, которая извлекается из опыта предшествующих измерений. Без априорной информации выполнение однократного измерения бессмысленно. Предварительно проводится тщательный анализ априорной информации. В ходе этого анализа уясняется физическая сущность изучаемого явления, уточняется его модель, определяются влияющие факторы. ^

Априо́ри (лат. a priori — буквально «от предшествующего») — знание, полученное до опыта и независимо от него (знание априори, априорное знание), т.е. знание, как бы заранее известное

Необходимым условием проведения однократного измерения является наличие априорной информации. К априорной относятся:

1. информация о виде закона распределения вероятно­сти показания и мере его рассеяния, которая извлекается из опыта предшествующих измерений;

2. информация о том, насколько значение измеряемой величины может отличаться от результата однократного измерения, которая может быть представлена классом точ­ности прибора;

3. информация о значении аддитивной и мультиплика­тивной поправки 9_i. Если значение поправки не известно,то оно учитывается ситуационной моделью, согласно кото­рой значение поправки может быть любым с одинаковой вероятностью в пределах от 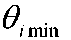до .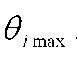

11. 5. Определение и свойства точечных оценок параметров

распределения: состоятельность, несмещенность, эффективность

Пусть  – некоторый параметр распределения FX (x, ).

Информация, необходимая для нахождения оценки ˆθ неизвестного

параметра , содержится в выборке Х1, …, Хn из данного

распределения. Таким образом, возникает задача построения оценки

ˆθ

параметра распределения как функции случайной выборки:

ˆθ

= ˆθ (Х1, …, Хn).

Заметим, что оценка параметра распределения является случайной

величиной (статистикой). В результате проведения эксперимента

(серии n независимых наблюдений) получают реализацию выборки –

числа x1, x2, …, xn. При этом оценка ˆθ принимает соответствующее

числовое значение ˆθ e =ˆθ (x1, x2,…, xn), которое является

приближенным значением неизвестного параметра . Оценки

указанного типа называют точечными, их применение целесообразно

14

при достаточно больших выборках. При малых объемах выборок

используют интервальные оценки, которые будут рассмотрены далее.

Ниже определяются свойства точечных оценок: состоятельность,

несмещенность, эффективность, каждое из которых определенным

образом характеризует меру близости оценки ˆθ (случайной

величины) к истинному значению (неслучайной величине)

неизвестного параметра  распределения FX (x, ). Понятно, что

вопрос обладает ли данная оценка каким-либо (или всеми) из

указанных свойств требует специального рассмотрения.

Состоятельность. Оценка ˆθ называется состоятельной оценкой

параметра , если оценка ˆθ по вероятности сходится к оцениваемому

параметру:  > 0 +

ˆθ

P (| θ | ε) 0 n     (символически это принято

записывать так:

ˆθ

θ

P

n   ). Иными словами, состоятельная оценка

обладает свойством: с увеличением объема выборки n уменьшается

вероятность того, что абсолютная величина отклонения оценки от

оцениваемого параметра  превзойдет любое наперед заданное  > 0.

Несмещенность. Оценка ˆθ называется несмещенной оценкой

параметра , если ее математическое ожидание равно оцениваемому

параметру: Mˆθ = .

Если Mˆθ  , то имеет место систематическая ошибка, величину

|Mˆθ – | называют смещением.

Оценка ˆθ называется асимптотически несмещенной, если

Mθˆ nθ 

В качестве упражнения докажем следующее утверждение:

Пусть ˆθ – несмещенная оценка параметра распределения ,

причем D[ˆθ ] + 0 n   , тогда ˆθ – состоятельна.

15

Запишем неравенство Чебышева:  > 0 0  2

P(|θˆ Mθˆ | ε) D[θˆ] ε

   .

Учтем, что по условию ˆθ – несмещенная оценка (Mˆθ = ), тогда,

переходя к пределу при n  , по теореме о сжатой переменной

имеем:

 > 0 ˆθP(| θ|ε) + 0 n   , то есть ˆθ – состоятельна:

ˆθ

n θ

P

  .

Эффективность. Оценку ˆθ называют эффективной оценкой

параметра  в классе оценок, имеющих дисперсию, если дисперсия ˆθ

минимальна. Из двух оценок, принадлежащих данному классу, более

эффективна та, которая имеет меньшую дисперсию.__

п.с 11 вопрос найти только это смог , придется в инете искать на самой паре.

13.

стандартным отклонением (средним квадратичным отклонением) — S:

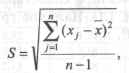
которое обычно и приводят при представлении результатов измерений (анализа) и которым характеризуют их воспроизводимость.

Стандартное отклонение, деленное на среднее выборки, называют относительным стандартным отклонением:

В общем случае метод анализа оптимален в той области содержаний, в которой и абсолютное (S) и относительное (S_r) стандартное отклонение имеют минимальные значения Ме́тод максима́льного правдоподо́бия или метод наибольшего правдоподобия (ММП, ML, MLE — Maximum Likelihood Estimation) в математической статистике — это метод оценивания неизвестного параметра путём максимизации функции правдоподобия^[1]. Основан на предположении о том, что вся информация о статистической выборке содержится в функции правдоподобия. Метод максимального правдоподобия был проанализирован, рекомендован и значительно популяризирован Р. Фишером между 1912 и 1922 годами (хотя ранее он был использован Гауссом, Лапласом и другими).

Пусть есть выборка из распределения , где  — неизвестные параметры. Пусть  — функция правдоподобия, где . Точечная оценка

называется оце́нкой максима́льного правдоподо́бия параметра . Таким образом оценка максимального правдоподобия — это такая оценка, которая максимизирует функцию правдоподобия при фиксированной реализации выборки.

Часто вместо функции правдоподобия используют логарифмическую функцию правдоподобия . Так как функция монотонно возрастает на всей области определения, максимум любой функции является максимумом функции , и наоборот. Таким образом

,

Если функция правдоподобия дифференцируема, то необходимое условие экстремума - равенство нулю ее градиента:

Достаточное условие экстремума может быть сформулировано как отрицательная определенность гессиана - матрицы вторых производных:

Важное значение для оценки свойств оценок метода максимального правдоподобия играет так называемая информационная матрица, равная по определению:

В оптимальной точке информационная матрица совпадает с математическим ожиданием гессиана, взятым со знаком минус:

15.

Критерий Пирсона, или критерий χ² (Хи-квадрат) — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки.

Статистика критерия

Для проверки критерия вводится статистика:

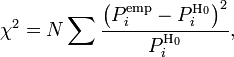
где  — предполагаемая вероятность попадания в -й интервал,  — соответствующее эмпирическое значение,  — число элементов выборки из -го интервала,  — полный объём выборки. Также используется расчет критерия по частоте, тогда:

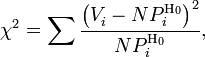
где  — частота попадания значений в интервал. Эта величина, в свою очередь, является случайной (в силу случайности ) и должна подчиняться распределению .

17.Критерии согласия.

8. Критерии согласия

Критериями согласия называют критерии, предназначенные для проверки простой гипотезы  при сложной альтернативе  . Мы рассмотрим более широкий класс основных гипотез, включающий и сложные гипотезы, а критериями согласия будем называть любые критерии, устроенные по одному и тому же принципу. А именно, пусть задана некоторая функция отклонения эмпирического распределения от теоретического, распределение которой существенно разнится в зависимости от того, верна или нет основная гипотеза. Критерии согласия принимают или отвергают основную гипотезу исходя из величины этой функции отклонения.

Итак, имеется выборка из распределения . Мы сформулируем ряд понятий для случая простой основной гипотезы, а в дальнейшем будем их корректировать по мере изменения задачи. Проверяется простая основная гипотеза при сложной альтернативе .

K1.

Пусть возможно задать функцию , обладающую свойствами:

а)

если гипотеза верна, то , где — непрерывное распределение;

б)

если гипотеза неверна, то при .

K2.

Пусть такая функция задана. Для случайной величины из распределения определим постоянную из равенства .

Построим критерий:

(22)

Мы построили критерий согласия. Он «работает» по принципу: если для данной выборки функция отклонения велика (по абсолютному значению), то это свидетельствует в пользу альтернативы, и наоборот. Убедимся в том, что этот критерий имеет (асимптотический) размер и является состоятельным.

Определение 29.

Говорят, что критерий для проверки простой гипотезы является критерием асимптотического размера , если его размер приближается к с ростом :

  при   .

Поскольку альтернатива всегда является сложной, то, как мы уже отмечали в замечании 16, вероятность ошибки второго рода любого критерия  есть функция  от конкретного распределения  из списка возможных альтернатив  . Или, при ином виде основной гипотезы, из числа распределений, отвечающих альтернативе  .

Определение 30.

Критерий для проверки гипотезы против сложной альтернативы называется состоятельным, если для любого распределения , отвечающего альтернативе , вероятность ошибки второго рода стремится к нулю с ростом объема выборки:

  при   .

Свойство 10.

Для критерия , заданного в (22), при :

1.

;

2.

для любого распределения , отвечающего .

Иначе говоря, построенный критерий имеет асимптотический размер и состоятелен.

19. Нормированние метрологических характеристик средств измерений.

21. Метрологическая надежность средств измерений

В процессе эксплуатации метрологические характеристики и параметры средства измерений претерпевают изменения. Эти изменения носят случайный монотонный или флуктуирующий характер и приводят к отказам, т.е. к невозможности СИ выполнять свои функции. Отказы делятся на неметрологические и метрологические.

Неметрологическим называется отказ, обусловленный причинами, не связанными с изменением MX средства измерений. Они носят главным образом явный характер, проявляются внезапно и могут быть обнаружены без проведения поверки.

Метрологическим называется отказ, вызванный выходом MX из установленных допустимых границ. Как показывают проведенные исследования [5], метрологические отказы происходят значительно чаще, чем неметрологические. Это обуславливает необходимость разработки специальных методов их прогнозирования и обнаружения. Метрологические отказы подразделяются на внезапные и постепенные.

Внезапным называется отказ, характеризующийся скачкообразным изменением одной или нескольких MX. Эти отказы в силу их случайности невозможно прогнозировать. Их последствия (сбой показаний, потеря чувствительности и т.п.) легко обнаруживаются в ходе эксплуатации прибора, т.е. по характеру проявления они являются явными

Постепенным называется отказ, характеризующийся монотонным изменением одной или нескольких MX.

С понятием "метрологический отказ" тесно связано понятие метрологической исправности средства измерений. Под ней понимается состояние СИ, при котором все нормируемые MX соответствуют установленным требованиям.

Способность СИ сохранять установленные значения метрологических характеристик в течение заданного времени при определенных режимах и условиях эксплуатации называется метрологической надежностью.

Надежность СИ характеризует его поведение с течением времени и является обобщенным понятием, включающим в себя стабильность, безотказность, долговечность, ремонтопригодность (для восстанавливаемых СИ) и сохраняемость.

Стабильность СИ является качественной характеристикой, отражающей неизменность во времени его MX. Она описывается временными зависимостями параметров закона распределения погрешности.

езотказностью называется свойство СИ непрерывно сохранять работоспособное состояние в течение некоторого времени. Она характеризуется двумя состояниями: работоспособным и неработоспособным.

Долговечностью называется свойство СИ сохранять свое работоспособное состояние до наступления предельного состояния. Работоспособное состояние — это такое состояние СИ, при котором все его MX соответствуют нормированным значениям. Предельным называется состояние СИ, при котором его применение недопустимо.

Ремонтопригодность — свойство СИ, заключающееся в приспособленности к предупреждению и обнаружению причин возникновения отказов, восстановлению и поддержанию его работоспособного состояния путем технического обслуживания и ремонта.

23.Основные понятия и определения в области стандартизации.

Данное понятие охватывает широкую область общественной деятельности , которая включает в себя научные ,технические ,хозяйственные, экономические ,юридические аспекты. Что бы так сказать повышать производительность ,прибыль государства ,нужны эти форма стандартизации. Если правильно поставить данную стандартизацию , то это поспособствует развитию специализации и кооперирования производства. У этого понятия есть свое понятие давайте его рассмотрим. Стандартизация – это установление и применение правил что бы упорядочить деятельность в определенной области на пользу и при участии всех сторон (условия использования, безопасность , соблюдение условий и.т.д).Ст. так будем её называть , основана на объединённых достижениях науки , техники и передового опыта.Она должна идти в 1 ногу с прогрессом. Так же Ст. Должа обеспечить возможно полное удовлетворения интересов производителя и потребителя, повышение труда , экономия расходов материалов , энергии, рабочего времени , а так-же самое главное это безопасность при производстве. Объектами СТ. обычно являются изделия , нормы , правила , требования , методы , термины и .т.д., которые имеют перспективу многократного применения в науке , технике , промышлености, и.т.д. Ст. Делится на 2 вида. Государственная ст.- это форма развития , которая осуществляется под руководством государственных органов на единых Г. Планам ст. Национальная ст. – проводится в масштабе государства без государственной формы руководства и Международная стандартизация – проводится специальными международными органами или группой государств с целью облегчения взаимной торговли. науки, техники. Есть такое понятие как стандарт которое устанавливается при стандартизации нормы. И так посмотрим что такое стандарт. Стандарт – это номраивно-технический документ по ст., который устанавливает комплекс норм , правил , требований к объекту ст и утверждённый органами правительства. Так же есть еще такое понятие как Технические условия - это номративо-тех документ по ст. который устанавливает комплекс требований к конкретным типам , маркам , артикулам и продукции.