Матрица рангов движения показателей

Наименование	Критериальный	Фактич. порядок движения по периоду
показателя	порядок движения	Т1	Т2	Т3	…	ТК
Показатель 1	1	X11	X12	X13	…	X1K
Показатель 2	2	X21	X22	X23	…	X2K
>Показатель 3	>3	X31	X32	X33	…	X3K
…	…	…	…	…	…	…
Показатель N	N	XN1	XN2	XN3	…	XNK

Четвертый этап заключается в сравнении двух ранговых рядов – критериального и фактического. Как известно, ранговые ряды отличаются друг от друга по двум основным характеристикам: вопервых, разностью между номерами отдельных показателей и, вовторых, инверсией одного полного ряда по отношению к другому. Для оценки близости фактического и нормативного порядков используются коэффициенты ранговой корреляции Спирмена (по отклонениям) и Кенделла (по инверсиям).

Коэффициент ранговой корреляции Спирмена рассчитывается следующим образом:

1. Для каждого показателя из списка вычисляется квадрат разности (отклонения)  между его местом (рангом) в нормативном упорядочении и рангом в фактическом упорядочении по формуле

Y_i = (X_i – X_k)²,  (3.2)

где  Y_i – разность между рангом iго показателя в критериальном упорядочении и в фактическом;

X_k – ранг показателя в критериальном упорядочении;

X_i – ранг показателя в фактическом упорядочении.

2. Подсчитывается сумма квадратов отклонений по всем показателям в рассматриваемом периоде времени и рассчитывается коэффициент Спирмена по формуле

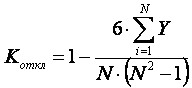,                                             (3.3)

Коэффициент ранговой корреляции Кенделла рассчитывается в несколько приемов.

Вопервых, для каждого показателя подсчитывается число других показателей, имеющих в критериальном упорядочении место, большее, чем место рассматриваемого показателя, а в фактическом упорядочении – ранг меньший, чем ранг рассматриваемого показателя:

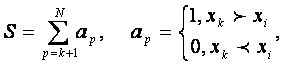,                         (3.4)

где k – место рассматриваемого показателя в критериальном упорядочении;

S – число инверсий для данного показателя;

p – места показателей, сравниваемых с рассматриваемым показателем;

N – число показателей, включенных в список характеристик системы;

a_p – функция, показывающая, находится или нет рассматриваемый показатель в инверсии с показателем, сравниваемым с ним (если да, то a_p = 1, в противном случае a_p = 0);

x_k (x_i) – ранг показателя в фактическом упорядочении, имеющего в критериальном упорядочении место k(p).

Вовторых, подсчитывается общее число инверсий по всем показателям и определяется коэффициент корреляции Кенделла:

, (3.5)

Оба коэффициента (К_откл, К_инвер) дают оценку близости данного рангового ряда к ряду, принятому за эталон (критериальный), на интервале от 1 до +1. Оценка +1 получается при совпадении фактического ряда с критериальным, а 1 при их полной разнонаправленности.

Интерпретировать значения описанных выше коэффициентов  можно следующим образом. Если их величины лежат в положительной области числовой оси, то в содержательном плане это свидетельствует о некотором улучшении структуры характеристик экономической системы и об увеличении эффективности ее работы. Если же значения коэффициентов отрицательны, то выбранная схема управления экономической системой приводит к отклонению ее структуры от оптимальной по принятому критерию и снижению эффективности ее функционирования. Вместе с тем это может свидетельствовать о значительном воздействии на систему внешних факторов, с которыми не в состоянии справиться ее механизм саморегуляции.

Показатель результирующей оценки близости фактической структуры движения показателей системы к критериальной (эталонной), основанный на двух коэффициентах ранговой корреляции для данного периода времени, можно рассчитать по формуле

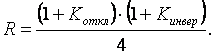,                                   (3.6)

Результирующая оценка показывает, насколько характер изменений в структуре связей системы отвечает выбранному критерию оценки. Иными словами, можно сказать, что этот показатель позволяет оценить эффективность принимаемых управленческих решений в соответствии с заданным критерием. Диапазон изменения этого показателя от 0 до +1. При этом 1 – полное совпадение изменений в структуре связей системы с выбранным критерием; 0 – полное несовпадение изменений в системе относительно выбранного критерия.

Участок, ограниченный по R^K в интервале времени ( t ₁, t_k ), отражает ситуацию, когда в любой момент времени потенциал экономического пространства используется полностью. Участок, ограниченный ломаными и кривой R в интервале  времени  (t₁, t_k),  отражает  реальную   оценку   использования   потенциала экономического пространства.

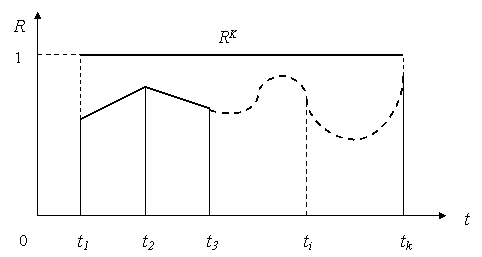
Рис. 3.7.Геометрическая интерпретация результативности использования экономического пространства

Величину этого уровня можно оценить соотношением площадей второго и первого участков. С учетом того, что R^K = 1, предлагается следующая простая формула:

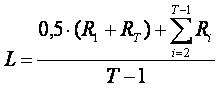  ,                              (3.7)

где T– число периодов времени.

         Чем лучше согласованы процессы, происходящие в региональном экономическом пространстве, тем большее значение будет иметь L (максимум L = 1, минимум L = 0).

Количественная оценка использования потенциала экономического пространства региона сформирована. Остановимся на качественной оценке, позволяющей сделать вывод о принадлежности экономического пространства региона к той или иной типологической группе (табл. 2.1).

Исходными данными для такой оценки будут ускорения движения показателей по каждому из блоков (табл. 3.1, 3.2, 3.4, 3.5). С учетом того, что показатели в каждом блоке подвергались процедуре ранжирования, необходимо использовать весовые коэффициенты для величин ускорения по каждому показателю. Существует достаточно много способов определения таких коэффициентов – от использования экспертных оценок до применения регрессионного анализа. Вес каждого показателя ускорения должен, с одной стороны, определяться его местом в блоке, с другой – зависеть от количества показателей в блоке. Для получения весовых коэффициентов, отвечающих этим требованиям, нами предлагается использовать экспоненциальную зависимость от числа, обратного порядковому номеру показателя в блоке:

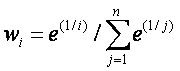,                                         (3.8)

где w_i – весовой коэффициент показателя, занимающего iе место в блоке;

е – основание натурального логарифма;

n – количество показателей в блоке.

         Для блоков, включающих до десяти показателей, числовые значения коэффициентов приведены в (табл. 3.8).

Таблица 3.8