15. Правила главных характеристик и гарантированный уровень решения.

Правило одной главной характеристики.

Среди характеристик вариантов решения выбирается та, которая обладает наибольшим приоритетом.

По остальным характеристикам решения назначаются требуемые ограничения, которые определяют допустимую область для принятия решения.

Вариант по этому правилу называется оптимальным, если он соответствует наилучшему значению главной характеристики и удовлетворяет ограничениям на остальные характеристики.

Правило легко применимо для выбора вариантов, является простым для расчетов, но является самым слабым по силе выбора и обладает адекватностью, соответствующей величине приоритета главной характеристики.

Правило двух главных характеристик.

Главными называются характеристики вариантов решения, обладающие наибольшими величинами коэффициентов приоритета.

Оптимальным по данному правилу называется вариант, у которого обе главные характеристики принимают наилучшие значения. Самыми приоритетными характеристиками являются характеристики затрат и некоторой эффективности решения.

Обычно ЛПР стремится уменьшить затраты на решение и увеличить его эффективность. При этом снижать затраты на решение до нуля, естественно, нельзя.

Поэтому по данному правилу возможны следующие формулировки критерия оптимального выбора:

• При заданных затратах на решение найти такой вариант, который обеспечивает максимум эффективности решения;

• Минимизировать затраты для достижения определенной эффективности решения;

По остальным характеристикам решения назначаются приемлемые для ЛПР ограничения.

Правило несложно для расчетов, широко применяется для выбора вариантов решения, но является менее сильным и менее адекватным проблеме, чем любое из правил принятия решения по полному множеству характеристик. Это правило можно расширить на большее число наиболее важных характеристик решения.

Правило гарантированного уровня.

Оптимальным по данному правилу называется такой вариант решения, который попадает в допустимую область решения.

Допустимая область определяется заданными ограничениями на характеристики решения.

Правило является простым для расчета, так как при этом требуется только перебор, сортировка вариантов и ряд итераций (повторов). Правило является обычным для проектных решений, успешно применяется и представляет собой реализацию требований технического задания на разработку проекта.

16. Правила квасе-паритета, взвешенных суммы и произведения характеристик.

Правило квазипаритета – правило паритета, преобразованное в правило паритета для дискретного (отдельного, прерывистого) множества вариантов.

(Правило паритета, то есть некоторого баланса приоритетов характеристик решения, разработано для непрерывного множества вариантов (баланс, равенство отношений)).

Линия заданного приоритета характеристик и их расчеты по правилу квазипаритета довольно просты. Правило позволяет учесть любые упорядоченные значения характеристик решения и обеспечивает однозначный выбор оптимального варианта при монотонных логических функциях решения.

Правило взвешенной суммы.

Оптимальным по правилу взвешенной суммы назовем вариант, который обеспечивает среди других вариантов решения максимум суммы произведений коэффициентов приоритета характеристик 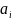на логические функции требований

µ(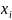 ), то есть обеспечивает

Мах∑ µ( )

Величины произведений µ( ) называют вкладами характеристик.

Смысл такого критерия выбора оптимального варианта состоит в том, чтобы учесть вклады в общую сумму тех характеристик вариантов решения, которые приняты к рассмотрению ЛПР.

Расчеты по данному правилу просты, принцип довольно широко применяется на практике в экономических задачах.

Выбор варианта решения по этому правилу обладает одним недостатком – маленькие вклады по важным характеристикам могут компенсироваться большими вкладами по характеристикам с малым приоритетом.

В результате применения этого правила лучше может оказаться вариант, обеспечивающий максимум суммы вкладов характеристик с низкими приоритетами, так как правило требует просто суммировать вклады характеристик.

Правило максимума взвешенного произведения.

Вариант решения по данному правилу называется оптимальным, если среди всех имеющихся вариантов он обеспечивает максимум произведения коэффициентов приоритета характеристик на логические функции требований µ( ), то есть обеспечивает

Мах П ( )

П - произведение логических функций ( ).

Такая форма критерия оптимальности обладает важной особенностью: если одна из величин µ( ) мала или равно 0, то величина всего критерия так же мала или равна нулю.

При использовании критерия взвешенной суммы вклад каждой характеристик в общую сумму только увеличивает ее значение.

Поэтому при использовании критерия взвешенного произведения говорят о его жесткости, так как он бракует любой вариант решения, который недостаточно удовлетворяет предъявляемым требованиям хотя бы по одной характеристике решении.

Это свойство формулируется в аксиоме выбора оптимальных решений:

Если значение какой-либо характеристики сравниваемого варианта решения не удовлетворяет требованиям задания, то и значение критерия взвешенного произведения тоже будет неудовлетворительным.

Правило несложно для расчетов особенно при равных приоритетах характеристик, обеспечивает однозначный выбор при монотонных величинах логических функций и довольно широко применяется на практике