24. 7 Методов количественного расчёта.
1 Метод. Экстраполяция
Экстраполяция (метод наименьшмх квадратов) означает прогноз по имеющимся данным вне границ изменения независимой характеристики «y».
Предположим, что имеется несколько результатов наблюдений за объектом управления по одной его характеристике y(x) для ряда значений x 1, x 2 ,…x n
Например,
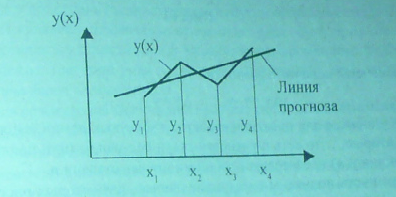
Линия прогноза может быть проведена «на глаз». Это может быть прямая, если нет никакой информации о характере этой линии. Лучшим способом построения линии прогноза является так называемый «метод наименьших квадратов» . Метод состоит в том, что линия прогноза проводится таким образом, чтобы сумма квадратов отклонений значений y(x)от значений, полученных опытным путем:y1,y2…yn. Была минимальна. Такая линия единственная и она лучше других экстраполирует имеющиеся данные.
2 Метод. Конечные разности
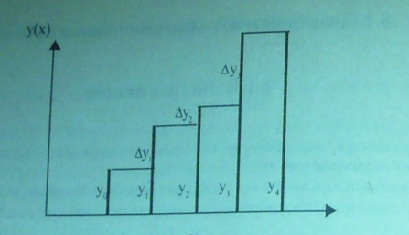
Важным и удобным для практики свойством конечных разностей является то, что если первые, вторые…, то есть n – разности стали постоянны (или практически постоянны), то функция y(x) представляет собой многочлен степени n.
Например, пусть получены следующие данные,для которых рассчитаны конечные разности:
-
Y
Дельта y
Дельта в квадрате y
2,0
2,24
24
2,56
32
8
2,96
40
8
Вторые разности, которые записаны в единицах последнего знака без нулей впереди, вычисляются как разности первых:
Дельта в квадрате у нулевое = дельта у 1 – дельта н нулевое
Дельта в квадрате у 1 = дельта у 2 – дельта у 1
Вторые разности по таблице постоянны, а это значит, что функция прогноза характеристики у в зависимости от х будет представлять собой многочлен степени 2. Это зависемость:
Y = х в квадрате – 3 х + 4
3 Метод Временный ряд
Временным рядом называют зависимость от времени на фоне ошибки (вида):
Y= y(t)+ E (t)
Где t – время процесса, а y(t)-прогнозируемая зависимость, E(t)- ошибка, зависящая от времени. Наиболее простым и распространенным путем выявления тенденции развития зависимости y (t) является сглаживание временного ряда. Одним из примеов сглаживания заключается в расчете скользящих средних. Применение скользящих средних позволяет сгладить периодические и случайные колебания и тем самым выявить имеющуюся тенденцию развития.
Метод скользящих средних состоит в том, что подсчитываются средние для меньшего числа имеющихся значений m<n
Например, сначала подсчитывается среднее для первых трех значений m=3
y̅ 1 = 1 /3 (y 1 + y 2 + y3)
Затем подсчитываем среднее для следующих трех значений временного ряда:
y̅ 2 = 1/3(y2+y3+y4)
Эта процедура повторяется до полного перебора значений ряда y(t)
Этот метод можно усовершенствовать путем введения весовых коэффициентов в расчетные выражения средних значений. Такое прием называется методом взвешенных скользящих средних.
