23. Принятие решений по экспериментальным данным на примере оценке прибыли турфирмы.
Существует зависимость Y – прибыли небольшой туристической фирмы от 2 факторов:
X1-количество сотрудников в агентстве, X2-уровень цен на туристические услуги.
Предположим, что кол-во сотрудников меняется от 3 до 6 человек, уровень цен колеблется от 90% до 110% от средних цен, а диапазон изменения прибыли колеблется от 50% до 100% по отношению к затратам.
Планирование эксперимента предполагает активное воздействие на исходные данные для рационального построения и использования на практике. Полагаем, что характеристики объекта могут поменяться: кол-во сотрудников и средний уровень цен на услуги. Из этого следует, что эксперимент можно организовать по активной схеме полного факторного эксперимента на 2 уровнях. Для этого перейдём от натуральных характеристик X1 и X2 к безмерным x1 и x2:
3 4 5 6
X1 - количество сотрудников
-1 0 1 2
x1 – безразмерная характеристика сотрудников
Интервал варьирования – 1 сотрудник.
Для второй характеристики имеем:
90% 100% 110%
X2 – уровень цен
-1 0 1
х2 – безразмерная характеристика уровня цен
Интервал варьирования 10%.
Теория планирования эксперимента говорит, что в новых осях можно построить следующую модель объекта:
Y=f(x1x2)=b0+b1x1+b2x2+b1,2x1x2
Коэффициенты модели b данном случае определяется по следующей схеме активного воздействия на объект:
№ |
X0 |
X1/x1 |
X2/x2 |
X1/X2 |
1 |
+ |
-/3 |
-/90 |
+ |
2 |
+ |
+/5 |
-/90 |
- |
3 |
+ |
-/3 |
+/110 |
- |
4 |
+ |
+/5 |
+/110 |
+ |
Коэффициенты b определяются по соотношению:
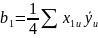
Таблица содержит столько столбцов, сколько надо определить коэффициентов в модели. Плюсы в таблице соответствуют 1, а минусы -1 для безразмерных характеристик искомой модели. В знаменателях стоят соответствующие значения натуральных характеристик.
Предположим, что наблюдения дали следующие результаты Y1 и Y2:
№ |
Y1 |
Y2 |
|
1 |
116 |
124 |
120 |
2 |
105 |
115 |
110 |
3 |
108 |
102 |
105 |
4 |
88 |
96 |
92 |
Полученные данные позволяют рассчитать коэффициенты модели:
b0 = ¼(120 + 110 + 105 + 92) = 106,75
b1 = ¼(-120 + 110 – 105 + 92) = 23
b2 = ¼(-120 – 110 + 105 + 92) = 33
b1 = ¼(120 + 110 + 105 + 92) = 106,75
b1,2 = ¼(120 – 110 – 105 + 92) = -3
Модель зависимости прибыли от числа сотрудников и уровня цен на услуги имеет вид:
Y = 106,75 + 23x1 + 33x2 – 3x1x2
Схема эксперимента позволяет следующим образом трактовать полученную модель.
Для 0-ых значений характеристик, т.е. для числа сотрудников 4 и 100% уровня цен на услуги прибыль равна 106,75%.
При 3 сотрудниках и 90% уровне цен (x1= - 1, х2= - 1) прибыль равна
Y = 106,75 - 23 - 33 – 3 = 53,75
При 5 сотрудниках и 90% уровня цен (x1= 1, х2= - 1)
Y = 106,75 + 23 - 33 + 3 = 99,75
При 3 сотрудниках и 110% уровня цен (x1= - 1, х2= 1)
Y = 106,75 - 23 + 33 + 3 = 119,75.
Эксперимент показал, что наилучшим вариантом решения будет наименьшее число сотрудников при наибольшем уровне цен.
Полученная модель позволяет решить 2-ую задачу: наибольшее влияние оказывает уровень цен (коэффициент b2 = 33), эффект числа сотрудников меньше (коэффициент b1 = 23). Взаимодействие числа сотрудников и уровня цен незначительное (коэффициент b1,2 = 3).