1.3. Примеры решения задач
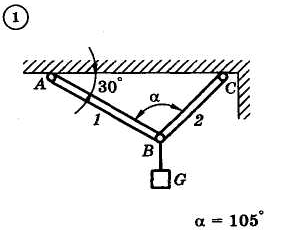
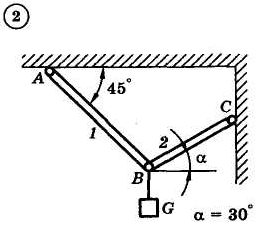
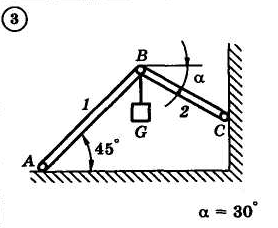
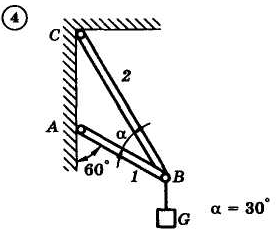
Задача 1.3.1. В шарнире В кронштейна АВС подвешен груз весом Р=100 Н. Определить усилия в стержнях кронштейна, если = 1100, =300, = 400. Стержни прикреплены к стене шарнирно (рис. 1.1, а).
Решение.
Аналитический
способ.
Объектом
равновесия следует считать шарнир В,
так как он объединяет оба стержня и
через него проходит линия действия
активной силы
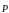(рис. 1.1, б).
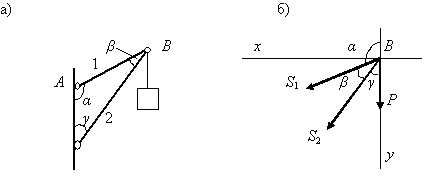
Рис. 1.1
Применяя принцип освобождаемости от связей, мысленно отбросим стержни и заменим их действие на шарнир В реакциями, считая при этом все стержни растянутыми (усилия направлены внутрь стержней). Активную силу перенесем вдоль линии действия и приложим в шарнире.
Так как все силы лежат в одной плоскости, то необходимо показать две координатные оси. Систему отсчета изобразим так, чтобы ее начало находилось в точке В, ось х направим горизонтально и влево, а ось y – вертикально и вниз.
К
объекту равновесия приложена система
сходящихся сил, поэтому для ее равновесия
необходимо и достаточно, чтобы
равнодействующая
этих сил равнялась нулю.
.
Для составления уравнений равновесия необходимо записать два уравнения проекций системы сил. Проекцией силы на какую-либо ось называется алгебраическая величина, равная произведению модуля силы и косинуса угла, который вектор силы образует с положительным направлением оси. Если угол, который сила образует с осью, острый, то проекция имеет знак «+», если тупой – то «–», если сила перпендикулярна оси, то ее проекция на данную ось равна нулю.
;
.
Определение
неизвестных величин.
Подставляя в уравнения равновесия
значения
и
,
а также используя формулу приведения
,
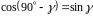запишем:
;
.
Тогда из первого выражения имеем
.
Произведя подстановку значения S1 во второе выражение, определим S2:
или
.
Зная
значение
,
находим
:
.
В результате усилие во втором стержне получено со знаком «–», это означает, что стержень 2 не растянут, а сжат. Положительное значение усилия в стержне 1 подтверждает правильность нашего предположения о том, что он растянут.
Графический
способ.
Изобразив в произвольном масштабе
вектор заданной силы
,
проводим через его начало и конец прямые,
параллельные независимым реакциям
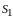и
,
причем не имеет значения, какую прямую
провести через начало заданной силы, а
какую – через ее конец (рис. 1.2). Точка
пересечения линий, параллельных
неизвестным реакциям, определяет третью
вершину треугольника.
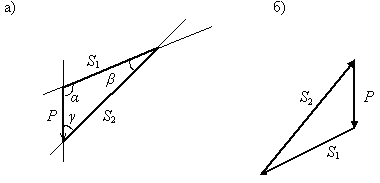
Рис. 1.2
Совершая
обход треугольника в направлении
заданной силы
,
показываем реакции стержней. Модули
и
определяются по теореме синусов.
откуда
В силовом треугольнике получаем истинное направление реакций: направлена так же, как и на расчетной схеме (рис. 1.2, б), то есть стержень 1 растянут, а реакция направлена в противоположную сторону, что означает – стержень 2 сжат.
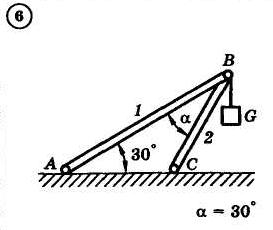
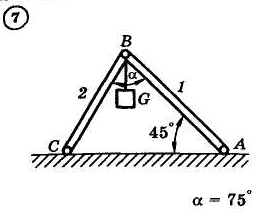
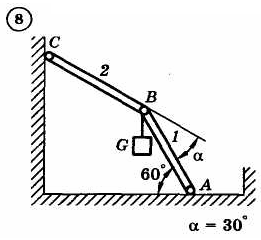
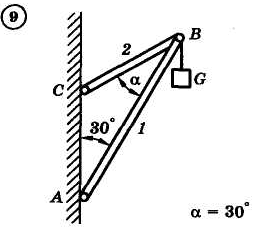
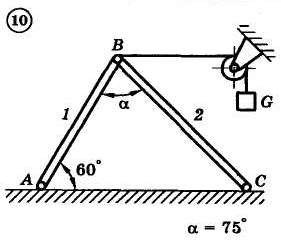
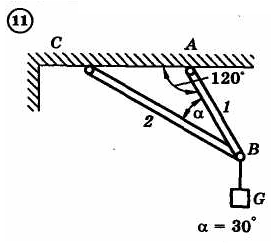
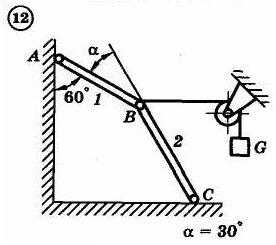
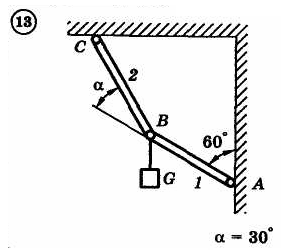
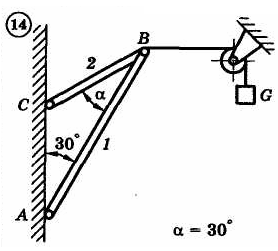
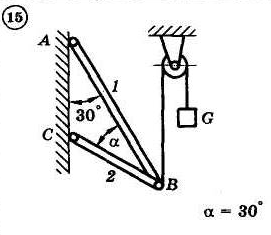
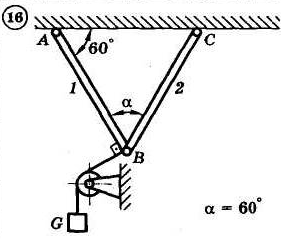
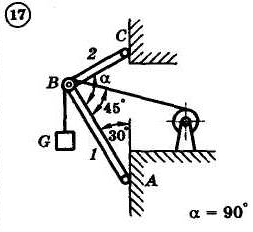
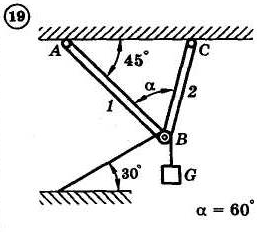
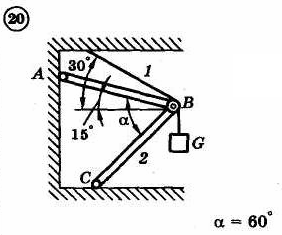
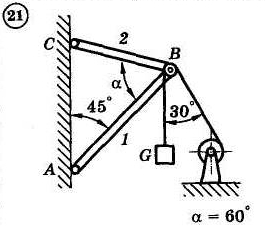
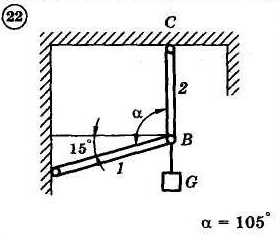
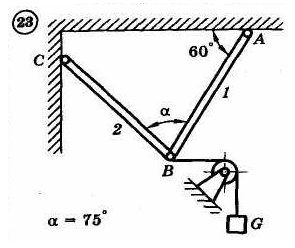
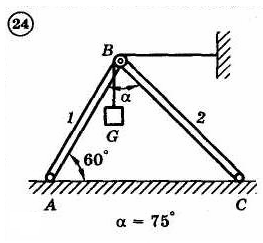
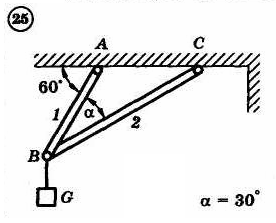
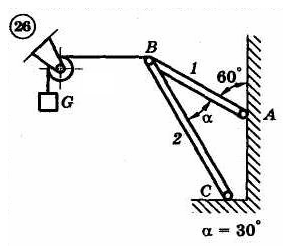
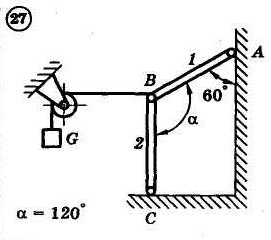
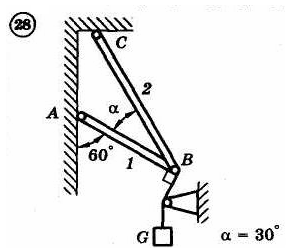
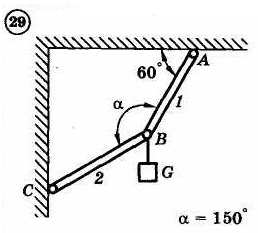
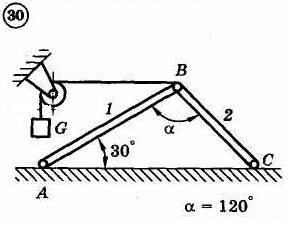
1.4. Задания с-1
Найти усилия в опорных стержнях 1 и 2 аналитическим и графическим способами. Вес груза G=10 кН.
