14.3. Примеры решения задач

Задача 14.3.1. К нижнему шкиву 3 подъемника (рис.14.1) приложен постоянный вращающий момент М. Определить ускорение груза 1 массы т₁, поднимаемого вверх, если масса противовеса 2 равна т₂, шкивы 3 н 4 массы т₃ каждый представляют собой однородные цилиндры радиуса r. Массой ремня и трением в подшипниках шкивов пренебречь.

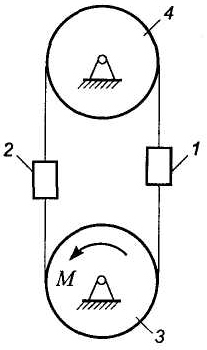
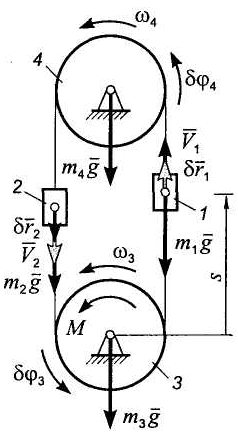
Рис. 14.1 Рис. 14.2

Решение. Система имеет одну сте­пень свободы, если тела, входящие в сис­тему, считать абсолютно твердыми, ре­мень нерастяжимым, а проскальзывание ремня на шкивах отсутствующим. При этих предположениях положение системы вполне определяется углом поворота ведущего шкива 3, который будем отсчи­тывать в направлении вращения шкива. Имея в виду цель задачи, примем за обобщенную координату перемещение s груза 1 (рис.14.2). Запишем уравнение Лагранжа

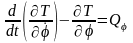. (14.2)

Вычислим кинетическую энергию системы как сумму кинетических энер­гий тел, входящих в ее состав,

.

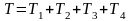Так как тела 1 и 2 движутся поступа­тельно, а тела 3 и 4 совершают враща­тельное движение, то

,

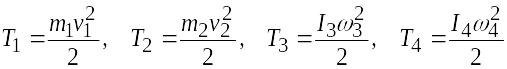где - скорости груза и противовеса, - угловые скорости шкивов, 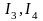- моменты инерции шкивов относительно их осей вращения.

Таким образом,

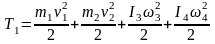. (14.3)

Запишем выражение (14.3) в обобщенных координатах. Заме­тив, что

,

получаем после подстановки последних формул в (14.3):

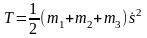. (14.4)

Таким образом, в рассматриваемом случае кинетическая энергия системы является функцией только обобщенной скорости.

Вычислим производные от кинетической энергии, входящие в уравнение (14.2):

(14.5)

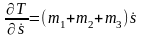, (14.6)

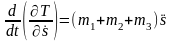. (14.7)

Найдем обобщенную силу. Заметив, что связи, наложенные на систему, являются идеальными, вычислим сумму работ вращающего момента и сил тяжести на перемещении системы из положения, в котором обобщенная координата равна нулю, в произвольное положение с координатой s > 0:

Поскольку 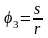, то

откуда

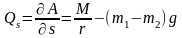. (14.8)

Подставляя формулы (14.5), (14.7) и (14.8) в уравнение (14.2), получаем дифференциальное уравнение движения системы

, (14.9)

из которого находим ускорение груза

.

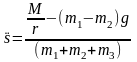Задача 14.3.2. Грузоподъемная установка (рис. 14.3) состоит из бараба­на 1 массой m₁= 200 кг и радиусом r= 0,2 м, невесомого нерастяжимого троса, который перемещает груз 2 по на­клонной плоскости, составляющий угол α = 30° с гори­зонтом. Масса груза т₂ = 1000 кг, коэффициент трения между грузом и наклонной плоскостью f = 0,2. К бараба­ну приложен вращающий момент М = 1,6 кНм. Опреде­лить величину ускорения груза а. Барабан считать одно­родным цилиндром.

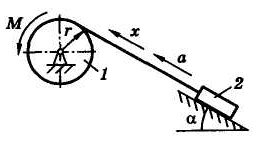
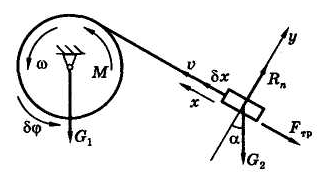
Рис. 14.3 Рис. 14.4

Решение. Рассматриваемая система имеет одну сте­пень свободы (s = 1) и может быть описана одним уравне­нием Лагранжа второго рода

В качестве обобщенной координаты выберем координа­ту х груза на наклонной плоскости q = x, тогда обобщенная скорость 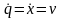будет являться скоростью груза.

Кинетическая энергия системы имеет вид

,

где ω — угловая скорость барабана; J — его момент инер­ции относительно оси вращения. Для однородного цилиндра

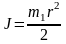
и, следовательно, J = 4 кгм².

При учете кинематической связи v = ωr, т. е. кинетическая энергия запишется в виде

.

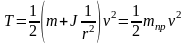где приведенная (к грузу) масса системы равна

кг.

Вычислим производные, входящие в левую часть урав­нения Лагранжа. Частная производная по обобщенной координате

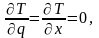
так как кинетическая энергия явно от координаты х не зависит. Частная производная по обобщенной скорости

.

Полная производная по времени

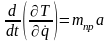
дает левую часть уравнения Лагранжа.

Входящую в правую часть уравнения обобщенную силу Q вычислим через возможную работу. Рассмотрим дей­ствующие в системе силы (рис. 14.4) и придадим телам системы возможное перемещение: бесконечно малое пере­мещение груза δх и поворот барабана на бесконечно ма­лый угол δφ. Соотношение между этими величинами мож­но получить из уравнения кинематической связи v = ωr. Интегрируя обе части этого уравнения по времени, находим

,

или

,

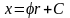где С — постоянная интегрирования.

Варь­ируя последнее соотношение, получаем равенство

,

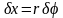которое в данном случае имеет простой геометрический смысл — равенство длины дуги окружности произведе­нию радиуса на величину угла в радианах.

На возможном перемещении работу будут совершать сила трения

,

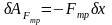сила тяжести груза

и вращающий момент

.

Таким образом, возможная работа для механической системы будет равна

,

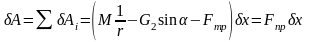где F_np — приведенная сила системы.

Поскольку для системы с одной степенью свободы воз­можная работа записывается в виде δА = Qδq, и в нашей задаче δq = δx, сравнивая последние два соотношения, находим Q = F_np, т. е. обобщенная сила является в данной постановке задачи приведенной силой

.

Вычислим ее, учитывая, что

.

Тогда

.

Составляем теперь уравнение Лагранжа, приравнивая правую и левую части: т_npа = F_np, откуда находим ускорение груза

.

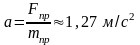Задача 14.3.3. В планетарном механизме, расположенном в гори­зонтальной плоскости, колесо 1 неподвижно (рис. 14.5). К рукоятке О₁О₃ приложен постоянный вращающий момент М. Определить уг­ловое ускорение рукоятки, считая колеса 2 и 3 однородными диска­ми с одинаковыми массами т и радиусами r. Массой рукоятки и сопротивлением пренебречь.

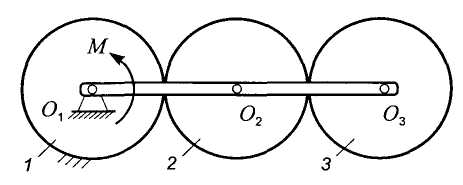
Рис. 14.5

Решение. Система имеет одну степень свободы. За обобщенную координату принимаем угол поворота рукоятки (рис. 14.6), тогда обобщенная скорость будет . Уравнение Лагранжа второго рода запишется в виде

. (14.10)

Кинетическая энергия системы равна сумме кинетических энер­гий колес 2 и 3:

. (14.11)

Предполагая, что колеса 2 и 3 совершают плоское движение, определяем их кинетические энергии по теореме Кёнига:

. (14.12)

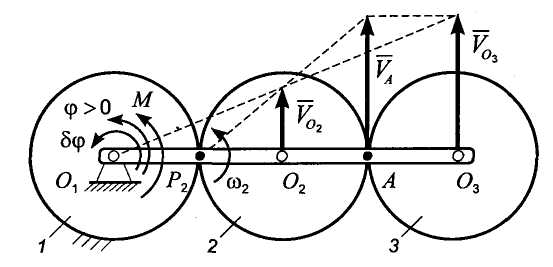
Рис. 14.6

Найдем скорости центров масс колес:

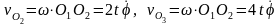. (14.13)

Угловую скорость колеса 2 определим с помощью мгновенного центра скоростей этого звена (точка 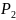, рис. 14.6):

. (14.14)

Колесо 3 движется поступательно, так как скорости его точек А и 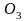равны, поэтому

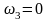. (14.15)

Моменты инерции колес

. (14.16)

Подставляя (14.12) в (14.11) с учетом (14.13)—(14.16), получаем кинетическую энергию системы как функцию обобщенной скорости

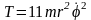. (14.17)

Вычислим производные от кинетической энергии системы, вхо­дящие в уравнение (14.10):

. (14.18)

Для определения обобщенной силы сообщаем рукоятке возмож­ное перемещение 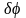и вычисляем сумму элементарных работ актив­ных сил на возможных перемещениях точек их приложения. Так как связи, наложенные на систему, являются идеальными, а механизм расположен в горизонтальной плоскости (поэтому работа сил тяже­сти колес равна нулю), то

,

откуда

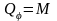. (14.19)

Подставив (14.18) и (14.19) в (14.10), получим дифференциаль­ное уравнение движения механизма

,

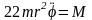из которого находим угловое ускорение рукоятки

.
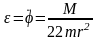