Реакции связей

Наименование связей	Условные обозначения и реакции	Примечание
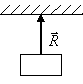
Опирание		Реакция связи направлена вдоль общей нормали к соприкасающимся поверхностям
Гибкие связи		Реакция направлена по касательной к гибкой связи в точку подвеса
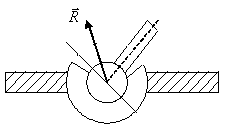
Сферический шарнир		Направление реакции зависит от действия других (активных) сил, при решении задач принято показывать три составляющие реакции
Нагруженный стержень		Реакция направлена вдоль стержня и проходит через центры шарниров, ограничивающих стержень
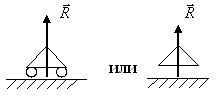
Шарнирно- подвижная		Реакция направлена по нормали к поверхности качения. В стержневой аналогии этот вид связи изображается в виде одного нагруженного стержня
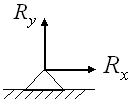
Шарнирно- неподвижная		Направление реакции зависит от действия других (активных) сил, при решении задач принято показывать две составляющие реакции. В стержневой аналогии связь изображается в виде двух нагруженных стержней
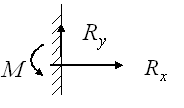
Жесткая заделка		Кроме составляющих реакций связи показывают пару сил с моментом М, который в этом случае называется реактивным

Сходящимися называются силы, линии действия которых пересекаются в одной точке.

Условие равновесия в геометрической форме : для равновесия системы сходящихся сил необходимо и доста­точно, чтобы силовой многоугольник, построенный для данных сил, был замкнутым.

Условия равновесия в анали­тической форме:

.

Если на тело действуют сходящиеся силы, лежащие в одной плоскости, то уравнений равновесия будет два.

При решении задач полезно использовать теорему о трех силах: если твердое тело находится в равновесии под действием трех непараллельных сил, то все три силы лежат в одной плоскости и ли­нии действия всех сил пересекаются в одной точке.

Алгоритм решения задач по статике сводится к такой последовательности действий.

1. Составление расчетной схемы.

1.1. Выбор объекта равновесия. При выборе объекта равновесия необходимо выяснить, к какому телу приложены задаваемые силы. Объект равновесия может иметь значительные размеры (балка) или очень малые, такие, которыми можно пренебречь (шарнир), и тогда объектом равновесия считают точку.

1.2. Изображение задаваемых сил и реакций связей.

1.3. Изображение системы отсчёта. Оси координат могут иметь любое направление, выбор их направления обусловлен характером задачи. Обычно ось х направляют вдоль горизонтальной оси балки вправо, а ось у вертикально вверх.

2. Определение условия равновесия.

3. Составление уравнений равновесия.

4. Определение искомых величин, проверка правильности решения и анализ полученных результатов.

Все расчёты при решении задач рекомендуется, как правило, производить в общем виде. Тогда для искомых величин будут получаться формулы, дающие возможность проанализировать полученные результаты.

При решении задач на равновесие несвободного твердого тела графическим способом удобно пользоваться, если число задаваемых сил и сил реакций связей, приложенных к твердому телу, находящемуся в равновесии, равно трем; при этом задача сводится к построению и решению силового треугольника. Силовой треугольник следует начинать строить с заданной силы.