12.5. Вопросы для самоконтроля (защиты контрольной работы)

1. Что называется кинетической энергией материальной точки?

2. Что называется кинетической энергией механической системы?

3. Сформулируйте теорему Кенига.

4. Получите формулы для вычисления кинетической энергии твердого тела при поступательном, вращательном и плоско­параллельном его движениях.

5. Как вычисляется работа силы упругости и силы тяжести?

6. На каких перемещениях работа силы тяжести а) положительна, б) отрицательна, в) равна нулю?

7. При каких условиях работа силы упругости положительна; отрицательна?

8. Как определяется работа постоянной по модулю и направле­нию силы на прямолинейном перемещении?

9. Чему равна работа постоянной по модулю и направлению силы трения скольжения?

10. Что называется мощностью силы?

11. Как определяется работа и мощность силы, приложенной к твердому телу, вращающемуся вокруг неподвижной оси?

12. Сформулируйте теорему об изменении кинетической энергии механической системы в дифференциальной форме (в форме мощностей).

13. Сформулируйте теорему об изменении кинетической энергии механической системы в конечной (интегральной) форме.

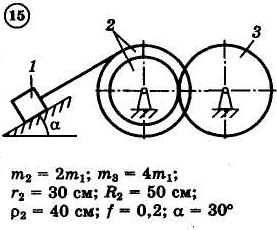
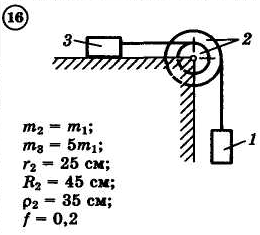
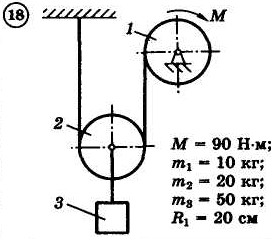
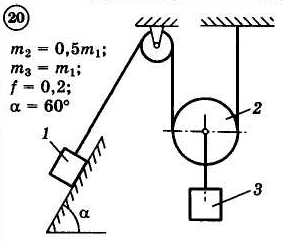
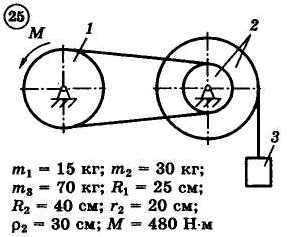
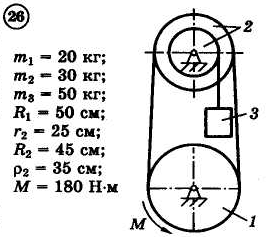
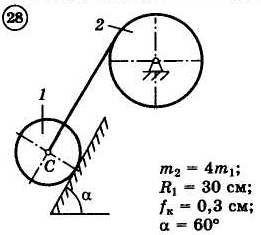
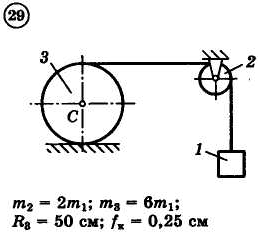
12.4.Задания

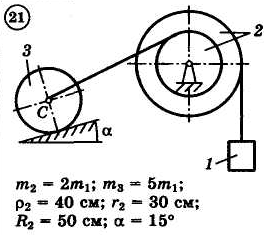
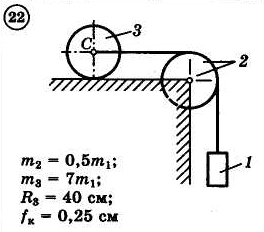
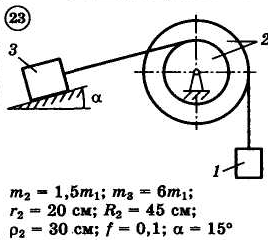
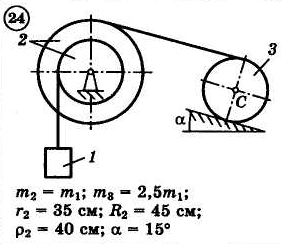
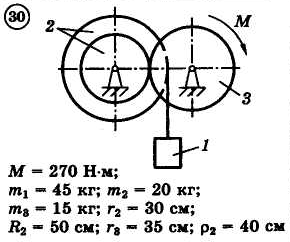
Для приведенных на схемах 1-30 механических си­стем, используя теорему об изменении кинетической энер­гии в интегральной форме, определить угловую скорость (варианты 4, 6, 7, 9, 11, 18, 25, 26, 28) или линейную скорость (остальные варианты) тела 1 после его заданного перемещения φ₁ = 2π рад или s₁ = 2 м. Движение начина­ется из состояния покоя.

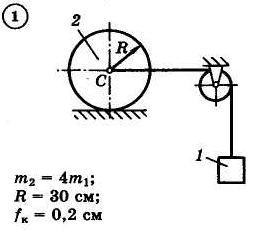
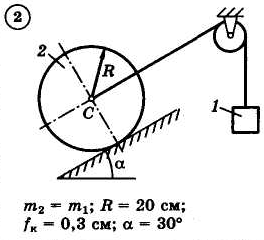
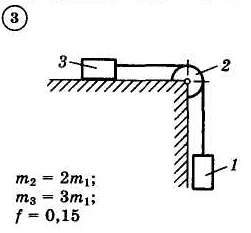
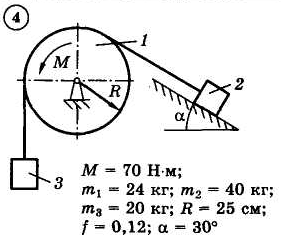
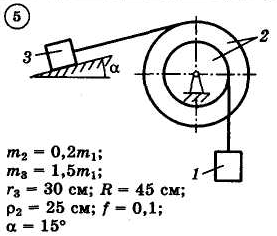
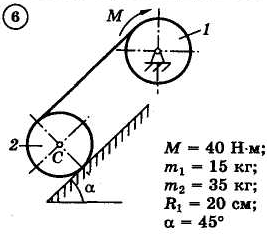
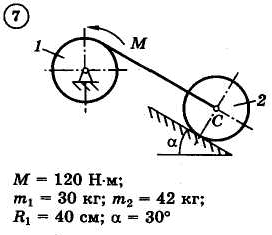
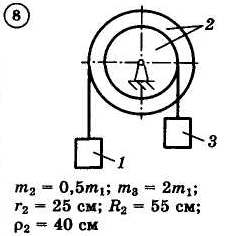
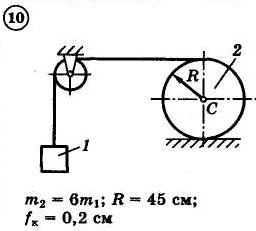
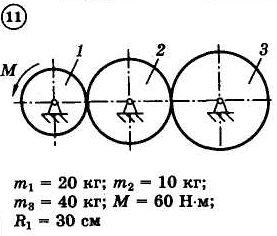
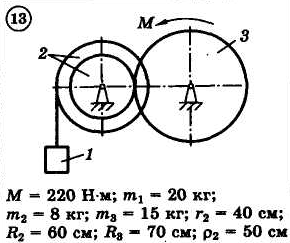
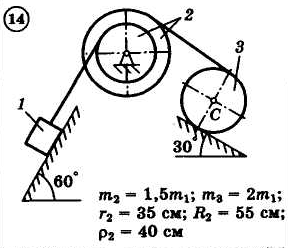
Д–13. Исследование движения механической системы с применением общего уравнения динамики

13.1. Цель: практическое освоение общего уравнения дина­мики как инструмента для состав­ления дифференциальных уравнений движения механических систем с одной степенью свободы.

13.2. Базовые понятия теории и методические рекомендации по решению задач

При движении механической системы в каждый момент времени сумма элемен­тарных работ активных сил и сил инерции на любом возможном перемещении системы равна нулю, т.е.

, (13.1)

где - активные силы, - силы инерции.

Уравнение (13.1) называют общим уравнением динамики, так как из него при различных дополнительных предположениях могут быть получены дифференциальные уравнения движения механиче­ской системы, общие теоремы динамики и т.п. В координатной форме уравнение (13.1) записывается в виде

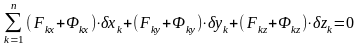, (13.2)

где F_kx, F_ky, F_kz - проекции активных сил на координатные оси; , , 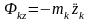- проекции сил инерции; , , - вариации координат точек приложения сил.

Задачи с помощью общего уравнения динамики рекомендуется решать в следующем порядке:

1. Определить число степеней свободы s рассматриваемой системы.

2. Выбрать независимые величины (обобщенные ко­ординаты), с помощью которых можно однозначно задать положение системы, т.е. назначить параметры, относительно которых будут составляться дифференциальные уравнения движения.

3. Изобразить на рисунке активные (задаваемые) силы и реакции неидеальных связей.

4. Приложить к телам (массам) системы силы инерции, напра­вив их в сторону, противоположную соответствующим ускорениям

5. Сообщить одной из точек системы возможное перемещение, изобразив его на расчетной схеме:

а) если в качестве обобщенной координаты выбрана линейная величина, то возможное перемещение следует сообщить той точке системы, положение которой определяет эта координата;

б) если в качестве обобщенной координаты принята угловая величина, то возможное перемещение следует сообщить тому телу, положение которого определяет эта координата;

6. Изобразить на расчетной схеме векторы возможных переме­щений точек приложения сил, указанных в п. 3 и 4.

7. Составить общее уравнение динамики; для этого следует вычислить и приравнять нулю сумму элементарных работ активных сил, реакций неидеальных связей и сил инерции на возможном пе­ремещении системы.

8. Подставить в уравнение п. 7 формулы для сил инерции из п. 4.

9. Выразить возможные перемещения точек приложения сил че­рез возможное перемещение, соответствующее выбранной координате системы.

10. Выразить ускорения точек приложения сил через обобщен­ное ускорение (вторую производную от обобщенной координаты по времени).

11. Подставив формулы, полученные в п. 9 и 10, в уравнение п. 8, получить после простых преобразований дифференциальное уравнение движения системы.

12. Дальнейшие действия зависят от цели, поставленной в задаче: а) решение закончено, если требовалось составить дифференци­альное уравнение движения;

б) если требуется найти закон движения системы, то далее следует проинтегрировать полученное дифференциальное уравнение при заданных начальных условиях;

в) если в задаче требуется определить ускорение какой-либо точки или угловое ускорение какого-либо тела (такая задача, как правило, ставится для систем, движущихся под действием постоян­ных сил), то искомую величину легко найти из полученного диффе­ренциального уравнения.