10.5. Вопросы для самоконтроля (защиты контрольной работы)

1. Сформулируйте основные законы механики.

2. Какая система отсчета называется инерциальной?

3. Запишите основное уравнение динамики.

4. От каких переменных могут зависеть силы, рассматриваемые в теоретической механике?

5. Запишите дифференциальное уравнение движения материальной точки в векторной форме.

6. Запишите дифференциальные уравнения движения матери­альной точки в проекциях на оси прямоугольной декартовой системы координат.

7. Запишите дифференциальные уравнения движения материальной точки в проекциях на естественные оси.

8. Сформулируйте первую задачу динамики для материальной точки.

9. Сформулируйте вторую задачу динамики для материальной точки и порядок ее решения.

Д–11. Исследование поступательного движения механической системы с применением теоремы о движении центра масс

11.1. Цели:

выяснить область применения общих теорем механики при исследовании динамического поведения механических систем;

приобрести практические навыки решения конкретных технических задач.

11.2. Базовые понятия теории и методические рекомендации по решению задач

А. Теорема о движении центра масс

Центром масс механической системы называется геометрическая точка С про­странства, определяемая радиус-вектором

,

где - масса системы.

Координаты центра масс определяются по формулам:

, 3(.2)

где x_k, y_k, z_k - координаты точки М_к .

Движение центра масс описывается уравнением

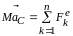, (11.1)

в котором - ускорение центра масс, - внешняя сила, дейст­вующая на точку М_k.

Формула (11.1) выражает теорему о движении центра масс:

Центр масс механической системы движется как матери­альная точка, в которой сосредоточена масса системы и к ко­торой приложены все внешние силы, действующие на систему.

При решении конкретных задач теорема о движении центра масс используется в проекциях на координатные оси:

(11.2)

Здесь х_с, у_с, z_с - проекции ускорения центра масс, a проекции силы .

Следствия из теоремы:

1. Если главный вектор внешних сил, действующих на систему, равен нулю, т.е. , то из (11.1) при этом следует, что или

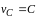, (11.3)

где - постоянный вектор, т.е. центр масс системы движется рав­номерно и прямолинейно.

2. Если проекция главного вектора внешних сил на какую-либо ось, например х, равна нулю, т.е. 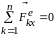, то проекция скорости центра масс на эту ось не изменяется при движении системы:

. (11.4)

Выражение (11.4) мож­но переписать в виде

. (11.5)

Б. Теорема об изменении количества движения

Количеством движения материальной точки называется произ­ведение массы точки на ее скорость, т.е. вектор .

Количеством движения механической системы называется вектор, равный сумме количеств движения точек системы.

, (11.6)

Количество движения системы связано со скоростью ее центра масс соотношением

, (11.7)

Формулы (11.6) и (11.7) используются при вычислении количест­ва движения системы в проекциях на координатные оси:

,

.

Уравнение, описывающее изменение количества движения сис­темы в зависимости от действующих на нее сил, может быть записа­но в двух формах: дифференциальной и интегральной (конечной).

Теорема об изменении количества движения в дифференциаль­ной форме имеет вид

, (11.9)

т.е. производная по времени от количества движения системы равна главному вектору всех внешних сил системы.

Теорема об изменении количества движения в интегральной форме имеет вид

, (11.9)

где - количества движения системы в моменты t₁ и t₂; - импульс силы за время t₂ –t₁.

При решении задач равенства (11.8) и (11.9) используются в проекциях на координатные оси:

.

Проекции импульса силы определяются по формулам

Следствия из теоремы:

1. Если главный вектор внешних сил, действующих на систему, равен нулю: , то из (11.8) следует, что

,

т.е. количество движения системы не изменяется при ее движении.

2. Если проекция главного вектора внешних сил на какую-либо ось, например х, равна нулю, т.е. , то проекция количества движения системы на эту ось не изменяется при ее движении:

.

Все многообразие задач, которые могут быть решены с помо­щью теоремы о движении центра масс и теоремы об изменении ко­личества движения, можно разделить на два типа:

1. Задачи, в которых движение центра масс системы известно; требуется определить неизвестную внешнюю силу, как правило, это реакция одной из связей.

2. Задачи, в которых имеет место сохранение движения центра масс в проекции на одну из осей. Искомыми величинами могут быть уравнение движения, скорость, перемещение какого-либо тела системы и т.п.

Рассмотрим порядок решения указанных задач.

А. Теорема о движении центра масс

Задачи первого типа (определение реакций связей) рекоменду­ется решать в следующем порядке:

1. Построить расчетную схему задачи:

изобразить схему рассматриваемой механической системы;

изобразить на ней все внешние силы, в том числе реакции внешних связей;

выбрать координатную систему; желательно, чтобы определяемая реакция связи была параллельной одной из координатных осей;

для определенности будем считать, что такой осью является координатная ось Ох.

2. Записать теорему о движении центра масс в проекциях на ось Ох; в это уравнение будет входить искомая реакция связи, проекции известных сил и величина .

3. Определить по исходным данным задачи величину , при этом, если в задаче известны движения тел, образующих рассматри­ваемую механическую систему, то следует использовать формулу

,

4. Из уравнения найти искомую реакцию и провести анализ полученного результата.

Задачи второго типа рекомендуется решать в следующем порядке:

1. Построить расчетную схему задачи:

изобразить схему рассматриваемой механической системы;

изобразить на ней все внешние силы, в том числе реакции внешних связей; выяснить особенности расположения внешних сил: в задачах рассматриваемого типа внешние силы образуют систему параллельных сил;

выбрать координатную систему, направив одну из осей пер­пендикулярно внешним силам; для определенности будем считать, что такой осью является координатная ось Ох.

2. Записав теорему о движении центра масс в проекциях на ось Ох, убедиться в том, что имеет место сохранение проекции на эту ось скорости центра масс.

3. Сформулировать начальные условия задачи

.

4. Дальнейшие действия зависят от того, какая величина является искомой:

если определяется, проекция скорости на ось Ох какой-либо точки системы, то (11.4) записывается в виде (11.5), постоянная интегрирования определяется по начальным условиям; из полученного соотношения можно найти искомую величину, если известны проекции скоростей остальных точек системы;

если определяется координата или проекция перемещения ка­кой-либо точки системы, то соотношение (11.4), записанное в виде (11.5), интегрируется; полученное таким образом конечное соотношение после определения постоянных интегрирования по начальным условиям служит для определения искомой величины.

Б. Теорема об изменении количества движения

Задачи первого типа (определение реакций связей) рекоменду­ется решать в следующем порядке:

1. Построить расчетную схему задачи:

изобразить схему рассматриваемой механической системы;

изобразить на ней все внешние силы, в том числе реакции внешних связей;

выбрать координатную систему; желательно, чтобы опреде­ляемая реакция связи была параллельной одной из координатных осей; для определенности будем считать, что такой осью является координатная ось Ох.

2. Записать теорему об изменении количества движения в про­екциях на ось Ох; в это уравнение будет входить искомая реакция связи, проекции известных сил и величина .

3. Вычислить проекцию количества движения системы на ось Ох и найти ее производную по времени.

4. Подставить производную от проекции количества движения на ось Ох и найти из полученного уравнения искомую реакцию связи. Провести анализ полученного результата.

Задачи второго типа рекомендуется решать в следующем порядке:

1. Построить расчетную схему задачи:

изобразить схему рассматриваемой механической системы;

изобразить на ней все внешние силы, в том числе реакции внешних связей; выяснить особенности расположения внешних сил: в задачах рассматриваемого типа внешние силы образуют систему параллельных сил;

выбрать координатную систему, направив одну из осей перпендикулярно внешним силам; для определенности будем считать, что такой осью является координатная ось Ох.

2. Записав теорему об изменении количества движения в проек­циях на ось Ох, убедиться в том, что имеет место сохранение проекции на эту ось количества движения системы:

.

3. Сформулировать начальные условия задачи.

4. Дальнейшие действия зависят от того, какая величина являет­ся искомой:

если определяется, проекция скорости на ось Ох какой-либо точки системы, то это можно сделать после определения постоянной интегрирования по начальным условиям;

если определяется координата или проекция перемещения ка­кой-либо точки системы, то соотношение п. 2 интегрируется;

полученное таким образом конечное соотношение после оп­ределения постоянных интегрирования по начальным услови­ям служит для определения искомой величины.