9.5. Вопросы для самоконтроля (защиты контрольной работы)

1. Какое движение точки называют сложным?

2. Какое движение точки называют абсолютным?

3. Какое движение точки называют относительным?

4. Какое движение точки называют переносным?

5. Сформулируйте и запишите теорему о сложении скоростей.

6. Сформулируйте и запишите теорему о сложении ускорений.

7. Что характеризует ускорение Кориолиса?

8. Как определить модуль вектора ускорения Кориолиса?

9. Сформулируйте правило Жуковского.

10. В каких случаях ускорение Кориолиса равно нулю?

11. Запишите теорему о сложении ускорений в случае поступа­тельного переносного движения.

Глава 3. Динамика

Д–10. Решение второй задачи динамики точки

10.1. Цель: приобретение практических навыков составления и интегрирования дифференциальных уравнений движения материальной точки.

10.2. Базовые понятия теории и методические рекомендации по решению задач

Движение материальной точки массы т под действием систе­мы сил (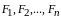 ), происходящее относительно инерциальной системы отсчета, описывается уравнением

, (10.1)

где - ускорение точки. Если точка является несвободной, то в правую часть соотношения (10.1) входят также реакции связей.

Поскольку 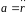, где - радиус-вектор точки, то уравнение (10.1) можно записать в виде

. (10.2)

Уравнение (10.2) называется дифференциальным уравнением движения материальной точки в векторной форме. При решении конкретных задач динамики материальной точки уравнение (10.2) записывается соответственно избранной системе координат.

Дифференциальные уравнения движения материальной точки в проекциях на оси прямоугольной декартовой системы координат имеют вид

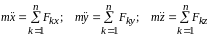, (10.3)

здесь - проекции ускорения точки, a - проекции силы на соответствующие оси координат.

Дифференциальные уравнения движения материальной точки в проекциях на оси естественного трехгранника записываются в форме

, (10.4)

где s - дуговая координата; - касательное уско­рение точки; v - модуль скорости; ρ - радиус кривизны траектории в данной точке; - проекции силы на касательную τ, главную нормаль п и бинормаль b соответственно.

С помощью дифференциальных уравнений движения матери­альной точки можно решать первую и вторую задачи динамики.

Первая (прямая) задача. Зная закон движения и массу точки, определить силу, действующую на точку.

Для решения этой задачи необходимо знать ускорение точ­ки. В задачах этою типа оно может быть задано непосредственно либо задан закон движения точки, в соответствии с ко­торым оно может быть определено.

Если движение свободной материальной точки массы т за­дано в прямоугольных декартовых координатах x=x(t), y=y(t), z = z(t), то первая задача динамики решается в следующем порядке:

1. Определяются проекции силы на оси х, у и z по формулам

. (10.5)

2. Вычисляется модуль силы

. (10.6)

3. Определяется направление силы с помощью направляющих косинусов

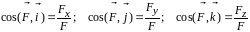. (10.7)

Вторая (обратная) задача.

Зная действующие на точку силы, ее массу и начальные условия движения, определить закон движения точки или какие-либо другие ее кинематические характеристики.

Начальные условия движения точки в декартовых осях — это координаты точки и проекции начальной скорости на эти оси в момент време­ни, соответствующий началу движения точки и принимаемый обычно равным нулю.

Решение задач этого типа сводится к составлению диффе­ренциальных уравнений (или одного уравнения) движения ма­териальной точки и их последующему решению путем непо­средственного интегрирования или с использованием теории дифференциальных уравнений.

Вторую задачу динамики рекомендуется решать в следующем порядке:

1. Выбрать систему координат.

2. Изобразить на расчётной схеме материальную точку в произ­вольном положении и действующие на неё силы, включая реакции связей (при несвободном движении точки).

3. Составить дифференциальные уравнения движения точки.

4. Записать начальные условия движения.

5. Построить общее решение дифференциальных уравнений движения.

6. Определить постоянные интегрирования по начальным усло­виям.

7. Подставив постоянные интегрирования в общее решение, оп­ределить закон движения точки.

При свободном движении материальной точки удобно пользо­ваться прямоугольной декартовой системой координат.

При криволинейном движении несвободной материальной точ­ки удобно составлять проекции дифференциальных уравнений на естественные оси.