
- •Введение
- •Образец титульного листа
- •Глава 1. Статика
- •1.2. Базовые понятия теории и методические рекомендации по решению задач
- •Реакции связей
- •1.3. Примеры решения задач
- •1.4. Задания с-1
- •1.5. Вопросы для самоконтроля (защиты контрольной работы)
- •Плоской произвольной системы сил
- •2.2. Базовые понятия теории и методические рекомендации по решению задач
- •2.3. Примеры решения задач
- •2.4. Задания с-2
- •2.5. Вопросы для самоконтроля (защиты контрольной работы)
- •Конструкции
- •3.2. Базовые понятия теории и методические рекомендации по решению задач
- •3.3. Примеры решения задач
- •3.4. Задания с-3
- •3.5. Вопросы для самоконтроля (защиты контрольной работы)
- •4.2. Базовые понятия теории и методические рекомендации по решению задач
- •4.3. Примеры решения задач
- •4.4. Задания с-4
- •4.5. Вопросы для самоконтроля (защиты контрольной работы)
- •5.2. Базовые понятия теории и методические рекомендации по решению задач
- •5.3. Примеры решения задач
- •5.4. Задания с-5
- •5.5. Вопросы для самоконтроля (защиты контрольной работы)
- •Глава 3. Кинематика
- •6.2. Базовые понятия теории и методические рекомендации по решению задач
- •Основные задачи кинематики:
- •6.3. Примеры решения задач
- •6.4.Задания к-6
- •6.5. Вопросы для самоконтроля (защиты контрольной работы)
- •7.2. Базовые понятия теории и методические рекомендации по решению задач
- •7.3. Примеры решения задач
- •7.4.Задания к–2
- •7.5. Вопросы для самоконтроля (защиты контрольной работы)
- •8.2. Базовые понятия теории и методические рекомендации по решению задач
- •8.3. Примеры решения задач
- •8.4. Задания к-8
- •8.5. Вопросы для самоконтроля (защиты контрольной работы)
- •9.2. Базовые понятия теории и методические рекомендации по решению задач
- •9.3. Примеры решения задач
- •1. Определение . По теореме о сложении скоростей имеем .
- •9.4. Задания к-9
- •9.5. Вопросы для самоконтроля (защиты контрольной работы)
- •Глава 3. Динамика
- •10.2. Базовые понятия теории и методические рекомендации по решению задач
- •10.3. Примеры решения задач
- •10.4. Задания д-10
- •10.5. Вопросы для самоконтроля (защиты контрольной работы)
- •11.2. Базовые понятия теории и методические рекомендации по решению задач
- •11.3. Примеры решения задач
- •11.4.Задания д – 11
- •11.5. Вопросы для самоконтроля (защиты контрольной работы)
- •Движения механической системы с использованием теоремы об изменении кинетической энергии
- •12.2. Базовые понятия теории и методические рекомендации по решению задач
- •12.3. Примеры решения задач
- •12.5. Вопросы для самоконтроля (защиты контрольной работы)
- •12.4.Задания
- •13.2. Базовые понятия теории и методические рекомендации по решению задач
- •13.3. Примеры решения задач
- •13.4. Задания
- •13.5. Вопросы для самоконтроля (защиты контрольной работы)
- •14.2. Базовые понятия теории и методические рекомендации по решению задач
- •14.3. Примеры решения задач
- •14.4. Задания д–6
- •14.5. Вопросы для самоконтроля (защиты контрольной работы)
9.3. Примеры решения задач
Задача 9.3.1. Тело D движется поступательно вдоль оси х так, что координата некоторой его точки меняется как xD = t3 + t2, м (рис. 9.1).
По
желобу ОА,
который представляет собой дугу
окружности радиуса R
= 20 м
тела движется точка М
так, что длина дуги |ОМ|
= s
= 5πt,
м.
Для момента времени t
= 1 с
определить абсолютную скорость
 и абсолютное ускорение
и абсолютное ускорение
 точки М.
точки М.
Решение.
1.
Определение
.
Согласно теореме о сложении скоростей,
абсолютная скорость равна векторной
сумме относительной и переносной
скоростей:
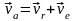 .
.
Относительную
скорость точки (скорость по отношению
к телу D)
находим, вычисляя ее алгебраическое
значение как производную от дуговой
координаты по времени:
 ,
и при t
= 1с
получаем
,
и при t
= 1с
получаем
 .
.
Чтобы определить направление этой скорости, следует установить, где находится точка М в данный момент времени.
Вычисляя
длину дуги |OM|t=1c=
5π
м,
определяем значение угла α:
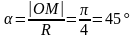 — точка М
находится в середине дуги ОА
(рис.9.2).
— точка М
находится в середине дуги ОА
(рис.9.2).
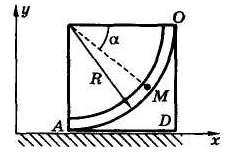
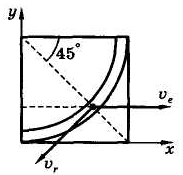
Рис. 9.1 Рис. 9.2
Скорость
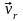 точки направляем по касательной к ее
траектории (окружности) в сторону
увеличения длины дуги, так как
алгебраическое значение скорости
положительно.
точки направляем по касательной к ее
траектории (окружности) в сторону
увеличения длины дуги, так как
алгебраическое значение скорости
положительно.
Переносной скоростью по определению будет скорость той точки тела D, с которой в данный момент времени совпадает точка М.
В имеющемся случае поступательного движения тела скорости всех его точек одинаковы (это скорость тела D), и тогда, поскольку движение прямолинейное, переносную скорость можно найти как производную от координаты:
 ,
,
и
при t=1
с
получаем
 =5
м/с.
Направлена она по оси х,
так как vex
> 0.
=5
м/с.
Направлена она по оси х,
так как vex
> 0.
Складывать
векторы
и
 удобнее всего с помощью проекций.
Проецируя равенство
на оси (рис. 9.2), получаем
удобнее всего с помощью проекций.
Проецируя равенство
на оси (рис. 9.2), получаем

и окончательно
 .
.
2. Определение . Согласно теореме Кориолиса, абсолютное ускорение равно векторной сумме относительного, переносного и кориолисова ускорений:
 .
.
В
данном случае кориолисова ускорения
 не будет, так как переносное движение
поступательное и его угловая скорость
ωе
= 0.
не будет, так как переносное движение
поступательное и его угловая скорость
ωе
= 0.
Относительное
ускорение
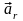 в общем случае будет складываться
из вращательного и центростремительного:
в общем случае будет складываться
из вращательного и центростремительного:
 .
.
Вращательное
относительное ускорение
 вычисляем через производную от
алгебраического значения скорости:
вычисляем через производную от
алгебраического значения скорости:
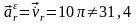 м/с
и
м/с
и
 .
.
Ускорение направлено туда же, куда и скорость так как знаки их алгебраических значений совпадают (ускоренное движение).
Центростремительное
относительное ускорение
 находим через скорость и радиус
кривизны траектории:
находим через скорость и радиус
кривизны траектории:
 .
.
Оно направлено к центру окружности желоба (рис. 9.3).
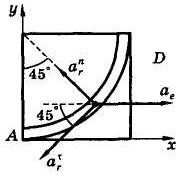
Рис. 9.3
Переносное ускорение (поскольку движение тела D поступательное и прямолинейное) ищем, дифференцируя найденную ранее переносную скорость
 ,
,
и
при t
= 1 с
имеем ае
= 8 м/с2.
Это ускорение совпадает по направлению
с
.
Проецируя на оси уравнение
 ,
получим проекции вектора абсолютного
ускорения:
,
получим проекции вектора абсолютного
ускорения:


И окончательно:

Задача 9.3.2. Тело D вращается в плоскости рисунка (рис. 9.4) вокруг оси Ох так, что его угол поворота равен
 рад.
рад.
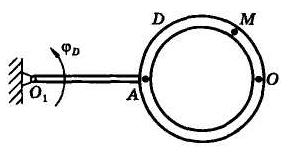
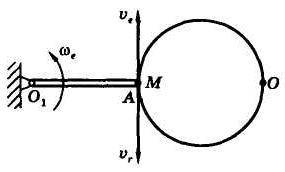
Рис. 9.4 Рис. 9.5
По желобу тела ОА движется точка М так, что алгебраическое значение длины дуги равно
ОМ =s = (25πt2 – 5πt) см.
Желоб является окружностью радиусом R = 20 см, расстояние |OA| = b = 10 см. Для момента времени t = 1 с определить абсолютную скорость и абсолютное ускорение точки М.
Решение.
