7.5. Вопросы для самоконтроля (защиты контрольной работы)

1. Перечислите основные виды движений твердого тела.

2. Какое движение твердого тела называется поступательным и какими свойствами оно обладает?

3. Какое движение твердого тела называется вращением вокруг неподвижной оси и как оно осуществляется?

4. По каким формулам определяются модули угловой скорости и углового ускорения вращающегося твердого тела?

5. Как направлены векторы угловой скорости и углового ускорения при вращении твердого тела вокруг неподвижной оси?

6. При каких условиях ускорение точки вращающегося тела составляет с отрезком , соединяющим точку с центром описываемой ею окружности, углы 0, 45, 90⁰?

7. Ускорения каких точек вращающегося тела:

а) равны по модулю,

б) совпадают по направлению,

в) равны по модулю и совпадают по направлению?

8). Каковы векторные выражения вращательной скорости, вращательного и центростремительного ускорений?

9). Что представляет собой передаточное число передачи и как определяется передаточное число сложной передачи?

К–8. Определение кинематических характеристик плоского механизма

8.1. Цель: отработка навыков решения задач по определению кинематических характеристик плоского движения твердого тела.

8.2. Базовые понятия теории и методические рекомендации по решению задач

Плоским или плоскопараллельным движением твердого тела называет­ся такое движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости.

Движение тела определяются тремя уравнениями, называемыми уравнениями плоского движения твердого тела:

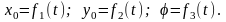
Скорость любой точки плоской фигуры равна геометрической сумме скорости полюса и скорости этой точки в ее вращении вместе с плоской фигурой вокруг полюса.

,

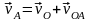где 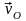- скорость полюса;

- скорость вращения точки вокруг полюса.

Следствие 1. Проекции скоростей точек плоской фигуры на ось, проходящую через эти точки, алгебраически равны.

Следствие 2. Концы скоростей точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между соответствующими точками отрезка.

При плоском движении плоской фигуры в каждый момент времени существует точка, связанная с плоской фигурой, скорость которой в этот момент равна нулю. Эту точку называют мгновенным центром скоростей.

Способы определения мгновенного центра скоростей.

1. Известны прямые, по которым направлены скорости двух точек плоской фигуры А и В (рис. 8.1). В этом случае мгновенный центр скоростей фигуры определится как точка пересечения перпендикуляров к этим прямым, восставленных в точках А и В.

2. Если скорости двух точек А и В плоской фигуры параллельны и не перпендикулярны АВ (рис. 8.2), то мгновенный центр скоростей находится в бесконечности (АР = ∞).

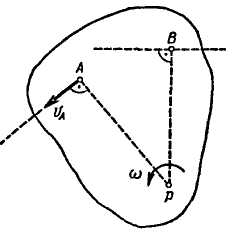
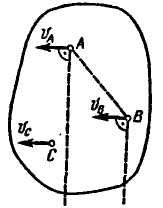
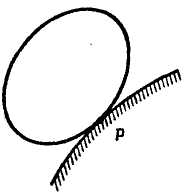
Рис. 8.1 Рис. 8.2 Рис. 8.3

3. Если плоская фигура катится без скольжения по некоторой неподвижной поверхности (рис. 8.3), мгновенный центр скоростей находится в точке соприкасания фигуры с поверхностью.

4. Если скорости точек А и В плоской фигуры параллельны между собой и перпендикулярны АВ, то для определения положения мгно­венного центра скоростей должны быть известны модули скоростей обеих точек А и В (рис. 8.4, а, б). Известно, что модули скоростей точек фигуры пропорциональны их расстояниям от мгновенного центра скоростей, т. е.

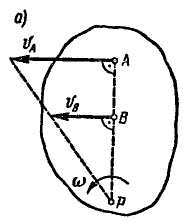
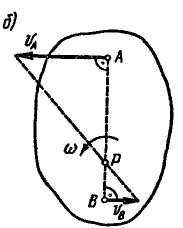
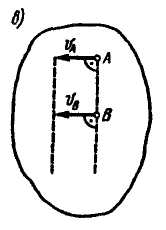
Рис. 8.4

Следовательно, концы скоростей точек А и В лежат на прямой, проходящей через мгновенный центр скоростей. Пересечение этой пря­мой с прямой АВ определяет мгновенный центр скоростей фигуры.

Если скорости точек А и В плоской фигуры равны, параллельны между собой и перпендикулярны АВ (рис. 8.4, в), то мгновенный центр скоростей находится в бесконечности (АР = ∞), а угловая скорость фигуры

Ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки в ее вращении вместе с плоской фигурой вокруг полюса:

,

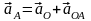а с учетом того, что ,

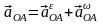будет ,

где 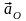- ускорение полюса; - вращательное ускорение точки.