6.3. Примеры решения задач

Задача 6.3.1. Точка М движется по своей траектории согласно уравнениям

х = t² см; у = sin πt см.

Определить траекторию точки М, ее скорость и ускорение в мо­мент времени t₁ = 1,5 с. Определить касательное и нормальное ускорения, а также радиус кривизны траектории.

Решение. Для определения траектории точки М исключим из уравнений движения время, после чего получим уравнение тра­ектории в виде

Определяем положение точки М в момент времени t₁ (рис. 6.2)

Для определения скорости точки М вычисляем первые производные от координат по времени, равные проекциям скорости точки на со­ответствующие оси координат:

.

Модуль скорости определяем по формуле

.

Вычисляем проекции вектора скорости точки на оси координат и её модуль в момент времени t₁

Направление вектора скорости определяем при помощи направ­ляющих косинусов

В момент времени t₁ направляющие косинусы вектора скорости

т.е. вектор скорости точки направлен параллельно оси Ох.

Для определения ускорения точки М вычисляем первые произ­водные от проекций скорости или вторые производные от координат по времени, равные проекциям ускорения точки на соответствую­щие оси координат:

.

Модуль ускорения определяем по формуле

Проводим вычисления для момента времени t₁

Направление вектора ускорения определяем при помощи на­правляющих косинусов

В момент времени t₁ направляющие косинусы вектора ускорения

Для определения касательного ускорения 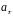точки М учтем, что его можно определить как проекцию вектора полного ускорения на направление касательной к траектории

.

В момент времени t₁

м/с².

Для определения нормальной составляющей вектора полного ускорения воспользуемся формулой

м/с².

В данной задаче вектор касательного ускорения совпадает с проекцией вектора полного ускорения на ось Ох, а вектор нормаль­ного ускорения - с проекцией ускорения на ось Оу.

Радиус кривизны траектории определяем, используя формулу для вычисления нормального ускорения

.

В момент времени t₁

м.

Изображаем все найденные величины на рис. 6.2.

Рис. 6.2

6.4.Задания к-6

При задании движения точки М координатным способом x = f₁ (t) и y = f₂ (t) определить: уравнение и вид траектории движения точки М, положение точки М на траектории в расчетный момент времени t₁; скорость точки М в любой момент времени t и в расчетный момент времени t₁; полное, касательное и нормальное ускорения точки М в любой момент времени t и в расчетный момент времени t₁; радиус кривизны траектории движения точки М;

Исходные данные приведены в таблице 6.1: вариант задания; уравнения движения точки М:

x = f₁ (t), (см), y = f₂ (t), (см);

расчетный момент времени t₁, (с) для определения положения точки М на траектории, скорости и ускорения точки.

Таблица 6.1

Вариант задания	Уравнения движения точки М			Расчетный момент времени t1, с
	x = f1 (t), см	y = f2 (t), см
1	x = 4t	y = 2t - 3t2	2
2	x = 1 - 4t2	y = - 3t	1
3	x = 2t2 + 4t + 1	y = 4t	1
4	x = 6t	y = - 2t2 - 4	1
5	x = t2 - 3	y = 5t	¼
6	x = t - 5	y = 6(t + 0,5t2)	2
7	x = t2	y = 2t - 1	1
8	x = 2 + 3t2	y = 4 - 3t	1
9	x = 4t2 + 1	y = 8t	1
10	x = 2t2 + 2	y = - 4t	½
11	x = 3 - 2t2	y = - 5t	½
12	x = 10t - 0,1t2	y = 5t	2
13	x = 3t	y = 4t - 5t2	2
14	x = 4t2 + 1	y = 12t - 3	2
15	x = 3t	y = 1 + 3t2	1
16	x = 3t2 + 5t	y = 5t	2
17	x = 4 - 2t	y = ( t + 1)2	1
18	x = 2t +2	y = 3t2 - 2	1
19	x = 10t	y = 4 + 5t2	2
20	x = 2t2	y = 4t - 1	¼
21	x = 5t	y = 4,9t2 – 5	1
22	x = 8t	y = 2t2 + 1	½
23	x = 1 - 2t2	y = 3t	1
24	x = -5t + 4	y = 2t2	1
25	x = 2 + sin ( /3)t	y = 1 + 3cos (/3)t	½
26	x = 2 + 3cos ( t)	y = 3sin ( t)	½
27	x = 4 sin ( /2)t	y = 3cos (/2)t	1
28	x = 8 cos ( /6)t	y = 8sin (/6)t	1
29	x = 4 cos ( /3)t	y = - 3sin (/3)t	1
30	x = 3 - 6 sin ( /6)t	y = 4 - 9cos (/6)tt	1