Основные задачи кинематики:

1. Установление закона движения тела по отношению к вы­бранной системе отсчета.

2. Определение по заданному закону движения тела кинема­тических характеристик этого движения: траектории, ско­рости, ускорения, угловой скорости и ускорения и т. д.

Движение точки считают заданным, если известен способ, позволяющий установить ее положение относительно выбранной системы отсчета в любой момент времени.

Существуют три способа задания движения точки: вектор­ный, координатный, естественный.

Векторный способ задания движения заключается в задании положения точки радиусом-вектором, который является век­торной функцией времени, относительно выбранной точки от­счета.

.

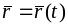Траектория точки М при век­торном способе — это геометриче­ское место точек концов радиуса-вектора при изменении времени, т. е. годограф радиуса-вектора.

Годограф — это кривая, которую описывает конец радиуса-вектора при изменении его аргумента, когда начало вектора находится в одной и той же точке .

Скорость точки характеризует быстроту и направление движения точки и равна производной радиуса-вектора точки по времени:

.

В механике производную по времени обозначают точкой над переменной.

Вектор скорости точки направлен по касательной к траектории точки в сторону ее движения .

Ускорение точки характеризует быстроту изменения величины и направления скорости точки и равно первой производной век­тора скорости по времени или второй производной радиуса-вектора по времени:

.

Вектор ускорения направлен по касательной к годографу вектора скорости.

Координатный способ задания движения заключается в зада­нии координат точки в виде известных, непрерывных, дважды дифференцируемых функций времени.

В декартовой системе коорди­нат уравнениями движения точки будут

.

Скорость точки в декартовых координатах:

,

где — проекции вектора скорости на соответствующие оси координат;

.

Углы вектора скорости с осями координат:

.

Ускорение точки в декартовых координатах:

,

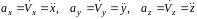( — проекции вектора ускорения на соответствующие оси координат):

.

Углы вектора ускорения с осями координат:

.

Естественный способ задания движения считается известным, если заданы:

1. Траектория точки.

2. Закон движения точки по траектории .

3. Начало отсчета.

4. Положительное и отрицательное направления движения.

Закон движения также называют дуговой координа­той, которую отсчитывают от начального положения. Дуговую координату не следует смешивать с длиной пути, пройденного точкой, так как за начало отсчета может быть выбрана любая точка или движение может быть колебатель­ным.

При естественном способе задания движения точки в качестве координатных осей принимают естественные оси (оси естественного трехгранника): — каса­тельная, 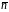— нормаль, 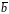— бинормаль.

Скорость точки ,

или

.

Ускорение точки

.

Ускорение точки состоит из двух взаимно перпендикулярных составляющих. Одна направлена по касательной к траектории, а другая - по нормали к этой траектории в сторону ее вогнутости. Эти составляющие называют соответственно касательным и нормальным ускорениями точки. Они лежат в со­прикасающейся плоскости. Проекция ускорения точки на би­нормаль равна нулю, так как вектор ускорения расположен в соприкасающейся плоскости (рис. 6.1):

.

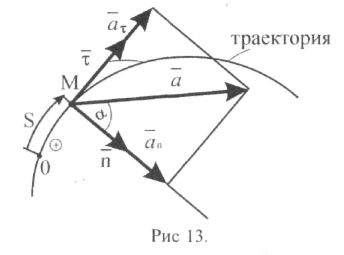
Рис. 6.1

Вектор касательного ускорения

,

модуль касательного ускорения

.

В ектор нормального ускорения

,

модуль нормального ускорения

.

Модуль ускорения равен:

.

Угол отклонения вектора ускорения от нормали составит (рис. 6.1):

.

Касательное ускорение характеризует изменение скорости по модулю, а нормальное — изменение скорости по направлению.

Касательное и нормальное ускорения точки можно определить при ее движении в плоскости через проекции скорости и ускоре­ния в декартовых координатах

,

.

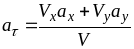Классификация движения по ускорениям

1. . Движение прямолинейное и равномерное.

2. . Движение криволинейное и равномерное.

3. . Движение криволинейное и равномерное.

4. . Движение криволинейное и неравномерное.

Уравнения движения точки

Уравнение равномерного движения по траектории любой фор­мы (V = const)

.

Уравнение равнопеременного движения по траектории лю­бой формы (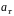 = const)

,

где — начальное положение; — начальная скорость.

Если > 0 , то движение равноускоренное.

Если < 0 , то движение равнозамедленное.

Скорость равнопеременного движения

.

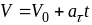Задачи целесообразно решать по следующему алгоритму:

1. Записать условие задачи.

2. Изобразить кинематическую схему.

3. Выбрать систему координат.

4. Составить кинематические уравнения движения точки, если они не заданы.

5. Выбрать метод решения задачи.

6. По известным соотношениям кинематики найти все величи­ны, требуемые по условию задачи.

7.Изобразить на схеме траекторию, скорость и ускорение точки.