Тема 8 измерение спектра и нелинейных искажений электрических сигналов

8.1 Общие сведения об анализе спектра

8.1.1 Общие принципы анализа спектра электромагнитных колебаний

Для решения ряда измерительных задач в различных областях исследование сигналов осуществляется не только во временной, но и в частотной (спектральной) областях. Анализ спектра сигналов может быть теоретическим (математическим) и экспериментальным. Приборы, предназначенные для экспериментального анализа спектра, называются анализаторами спектра.

Характеристики, описывающие свойства сигнала при частотном представлении, называются спектральными. Эти характеристики показывают распределение амплитуд или мощностей и фаз по частотам (между амплитудой и мощностью существует однозначная связь).

В основе спектральных методов лежит преобразование Фурье для временной функции, описывающей исследуемый сигнал. Разложение в ряд Фурье сигнала сложной формы позволяет представить сигнал в виде суммы гармоник, каждая из которых имеет свое амплитудное значение, частоту и фазу:

Ux (t) = A₀ + =

= A₀ + , (8.1)

где Сn = = Cn (ω) – амплитудный спектр, а

ϴn = arctg An/Bn = ϴn(ω) – фазовый спектр сигнала.

В практике электрорадиоизмерений наибольший интерес представляет амплитудный спектр, который называют просто спектр.

Как видно из (8.1), спектры периодических сигналов являются дискретными. Они образуются равноотстоящими спектральными линиями (гармониками) с частотными интервалами между соседними линиями, определяемыми периодом повторения сигнала Тх. Форма огибающей спектра определяется только формой сигнала и не зависит от периода повторения. При увеличении Тх спектральные линии сближаются и при Т → ∞ образуют сплошной спектр. Этот случай соответствует непериодическому сигналу или одиночному импульсу, для определения которого необходимо перейти от ряда Фурье к интегралу Фурье

Ux (t) = e^jωt dω (8.2)

Выражение (8.2) называют обратным преобразованием Фурье, позволяющим по известному амплитудному S(jω) и фазовому спектру ϴ(jω) восстановить исследуемый сигнал. При известном исследуемом сигнале Ux (t) можно определить его спектр. Для этого необходимо перейти к прямому преобразованию Фурье

S(jω) = e^-jωt dt, (8.3)

П ример формы амплитудного и фазового спектров прямоугольного видеоимпульса изображен рис. 8.1, а и радиоимпульса – на рис. 8.1, б.

Рис. 8.1. Спектры одиночных импульсов

Как видно из рис. 8.1, основная часть энергии сигнала сосредоточена в главном лепестке спектра. Поэтому задача анализатора спектра – это воспроизвести главный лепесток и по возможности еще несколько боковых лепестков спектра сигнала.

Для реализации такой задачи существуют различные методы, которые будут рассмотрены ниже.

8.1.2 Основные методы анализа спектра электромагнитных колебаний

Для анализа спектра электромагнитных колебаний используются различные методы, основными из которых являются:

фильтровые методы, реализующие метод фильтрации;

дисперсионные методы, базирующиеся на дисперсионно-временном методе анализа;

рециркуляционные методы, реализующие так называемый рециркуляционный (интерференционный) метод;

цифровые, использующие алгоритм дискретного преобразования Фурье (ДПФ).

Фильтровой метод анализа спектра

Фильтровой метод анализа спектра состоит в выделении спектральных составляющих сигнала с помощью узкополосного фильтра. Данный метод может быть реализован путем параллельного (одновременного) или последовательного анализа. Параллельный анализ осуществляется с помощью ряда узкополосных фильтров, каждый из которых выделяет одну составляющую спектра. Последовательный анализ состоит в выделении отдельных составляющих спектра либо с помощью одного узкополосного перестраиваемого фильтра, либо путем такого преобразования сигнала, при котором в полосу пропускания фильтра поочередно попадают спектральные составляющие сигнала с различными частотами.

При параллельном анализе необходимое количество фильтров n определяется частотным диапазоном (полосой анализируемых частот) Δf = fmax – fmin и полосой пропускания отдельного фильтра 2Δfф (рис. 8.2). В этом случае число фильтров определится по формуле

n = Δf/2Δfф (8.4)

В идеальном случае полоса пропускания отдельного фильтра 2Δfф определяет разрешающую способность анализатора спектра

Δfр = 2Δfф. (8.5)

Но такое может быть только при идеальной прямоугольной частотной характеристике фильтра.

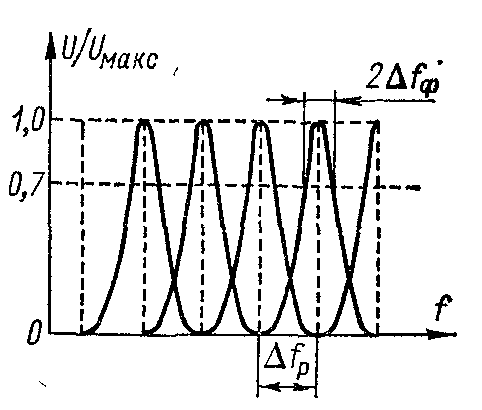
Рис. 8.2. К определению разрешающей способности анализатора спектра

На практике можно говорить лишь о приближении к идеальной частотной характеристике прямоугольной формы. Поэтому считают Δfф = qΔfф, где q > 1. Отсюда, разрешающая способность анализатора определится по формуле

Δfр = 2qΔfф. (8.6)

От разрешающей способности анализатора зависит такой важный параметр, как скорость анализа спектра

V = n/Δf²ф (8.7)

Как видно из формулы (8.7), скорость анализа резко снижается при сужении полосы пропускания фильтра.

Параллельный метод анализа спектра обладает такими достоинствами как малое время анализа и возможность анализа спектра одиночных импульсов. Однако из-за сложности реализации системы фильтров такой метод не получил широкого распространения.

Более широко распространен последовательный метод анализа спектра, сущность которого состоит в следующем. Входной сигнал, спектр которого необходимо измерить, без преобразования подается на узкополосный фильтр, частоту настройки которого можно изменять. В результате этого на выходе фильтра последовательно будут появляться гармонические составляющие спектра входного сигнала, интенсивность которых может быть измерена с помощью различного вида индикаторов (от обычных вольтметров среднеквадратического значения до осциллографических). Значения частот гармоник при этом могут быть считаны со шкалы перестройки фильтра.

Такой метод обладает рядом недостатков, например, невозможностью перестраивать фильтр в широких пределах без ухудшения его селективных свойств, а также процесс анализа не автоматизирован и занимает достаточно большое время.

Более распространенным методом является последовательный метод с преобразованием частоты (рис. 8.3).

Рис. 8.3. К реализации последовательного метода анализа спектра с преобразованием частоты.

Входной сигнал в виде радиоимпульсов частоты fсигн. в данной схеме поступает на вход преобразователя частоты ПЧ. На второй вход ПЧ подается напряжение гетеродина с частотой fгет. На выходе ПЧ образуются радиоимпульсы длительностью τ, с частотой заполнения fпч =fсигн.- fгет. (рис. 8.4).

Рис. 8.4. Временные диаграммы к методу последовательного анализа спектра

Данные импульсы поступают в усилитель промежуточной частоты (УПЧ), где последовательно будут попадать в его полосу пропускания. С выхода УПЧ будут сниматься усиленные радиоимпульсы с частотой заполнения, равной fпч. После детектирования и усиления эти уже видеоимпульсы подаются на пластины Y осциллографического индикатора. На пластины Х при этом будет подаваться напряжение генератора развертки. Учитывая то, что генератор развертки управляет работой гетеродина (осуществляет частотную модуляцию колебаний гетеродина), можно считать горизонтальную развертку осью частот. Таким образом, на экране ЭЛТ будут наблюдаться составляющие спектра входного сигнала в виде выбросов, имеющих конечную ширину, которая определяется формой амплитудно-частотной характеристики УПЧ. Амплитуда этих выбросов будет пропорциональна спектральной плотности импульсов промежуточной частоты, а их огибающая будет представлять собой спектральную характеристику исследуемого сигнала.

Разрешающая способность при последовательном анализе определяется также, как и при параллельном. В качестве полосы пропускания фильтра здесь применяется полоса пропускания фильтра УПЧ .

Время анализа для последовательного метода зависит от ширины исследуемой области частот и избирательности фильтра УПЧ. Если время анализа в полосе частот фильтра УПЧ составляет τа = 1/Δfпч, то полное время анализа в диапазоне частот Δf=fв – fн будет в Δ f /Δfпч раз больше, т.е.

Та посл. = = (8.8)

Как видно из формулы (8.8), при уменьшении ширины пропускания анализирующего фильтра, время анализа резко увеличивается. Поэтому для обеспечения разрешающей способности в несколько Гц последовательный анализ не применяется.

Дисперсионно-временной метод

Дисперсионный метод анализа спектра основан на использовании особенностей распространения радиосигналов в замедляющих системах с дисперсией фазовой скорости – дисперсионных линиях задержки (ДЛЗ). За счет дисперсии различные составляющие спектра будут задерживаться на различные интервалы времени и появляться на выходе линии задержки последовательно со сдвигом во времени. Если время задержки ДЛЗ линейно зависит от частоты, распределение энергии сигнала на выходе такой линии будет однозначно связано с ее частотой.

Фильтровой метод может быть реализован с помощью анализаторов спектра параллельного, последовательного или комбинированного действия. Рассмотрим работу анализатора спектра параллельного действия. Структурная схема такого анализатора изображена на рис. 8.2.

Рис. 8.2. Анализатор спектра параллельного действия

Работает такая схема следующим образом. Исследуемый сигнал после входного устройства ВУ подается одновременно на n фильтров, каждый из которых выделяет узкую полосу частот и имеет на выходе квадратичный детектор и индикатор. Фильтры Фi в общем случае должны перекрывать исследуемый диапазон частот и иметь равномерную расстройку и прямоугольные полосы пропускания. Если равномерную расстройку осуществить достаточно легко, то обеспечить прямоугольность полосы пропускания сложно. Особенно с ростом частоты. Кроме того, из-за многоканальности анализаторов приходится усложнять схему, применяя большое число фильтров, индикаторов и т.д. Поэтому такие анализаторы спектра не нашли широкого применения.

Более распространены анализаторы спектра последовательного действия (рис. 8.3), которые могут быть без преобразования частоты или с преобразованием частоты исследуемого сигнала.

Рис. 8.3. Структурная схема анализатора спектра последовательного действия без преобразования частоты

Как видно из структурной схемы, такой анализатор спектра представляет собой приемник прямого усиления. Входной сигнал поступает на входную цепь и с нее на фильтр Ф. Фильтр перестраиваемый и может выделять гармоники в зависимости от частоты настройки. Выделенная таким образом гармоника поступает на детектор Д, где происходит ее преобразование в сигнал постоянного тока, амплитуда которого пропорциональна амплитуде выделенной гармоники. Под воздействием данного сигнала срабатывает индикатор И, в качестве которого может быть амперметр, вольтметр или электронно-лучевая трубка. Таким образом, перестраивая фильтр в необходимых пределах, можно исследовать поочередно (последовательно) все гармоники входного сигнала.

Недостатком такого метода является невозможность перестраивать фильтр в широких пределах без ухудшения его селективных свойств. Кроме того, процесс анализа не автоматизирован и занимает достаточно большое время.

О т указанных выше недостатков позволяет избавиться схема последовательного анализатора спектра с преобразованием частоты (рис. 8.4).

Рис. 8.4. Структурная схема анализатора спектра последовательного действия с преобразованием частоты

Как видно из рисунка, такой анализатор состоит из супергетеродинного приемника и осциллографического индикатора. Входной сигнал поступает на входное устройство ВУ и с него на смеситель СМ. На второй смеситель подается сигнал от гетеродина, который представляет собой генератор качающейся частоты ГКЧ. ГКЧ изменяет свою частоту по линейному закону и тем самым переносит спектр входного сигнала в низкочастотный диапазон автоматически без участия оператора. Кроме того, он управляет работой генератора развертки ГР. В результате этого на экране осциллографического индикатора формируется линия горизонтальной развертки синхронно с изменением промежуточной частоты на выходе смесителя. Поэтому горизонтальную развертку можно считать осью частот.

Сигнал с выхода смесителя подается на усилитель промежуточной частоты УПЧ и с него на детектор Д, где преобразуется в сигнал постоянного тока и подается после усиления в усилителе вертикального отклонения УВО на пластины Y осциллографа. Т.к. процесс синхронизирован, то на индикаторе будут наблюдаться спектральные линии гармоник входного сигнала, причем каждая гармоника будет занимать место на горизонтальной оси, соответствующее значению своей частоты.

Недостатком такой схемы является трудность создания ГКЧ, работающего в широком диапазоне частот, который устраняется созданием комбинированных анализаторов спектра (рис. 8.5).

Рис. 8.5. Структурная схема комбинированного анализатора спектра

Как видно из рисунка 8.5, входной сигнал после входного устройства поступает на смеситель СМ1. На второй вход смесителя поступает сигнал от гетеродина Г. В результате спектр входного сигнала переносится в более низкочастотный диапазон, что упрощает конструкцию ГКЧ, который в данном случае работает в качестве второго гетеродина и не требует его широкой перестройки. Сигнал ГКЧ смешиваясь с сигналом первой промежуточной частоты, формирует разностные частоты, которые передвигаются по оси частот по закону изменения частоты ГКЧ. При этом они последовательно попадают в полосы пропускания фильтров Ф и через электронный ключ попадают на индикатор И, в качестве которого может также быть осциллографический индикатор И. На индикаторе при этом наблюдается изображение спектра исследуемого сигнала.

Основные характеристики анализаторов спектра

Анализаторы спектра характеризуются определенными параметрами, определяющими их основные метрологические качества. Система данных параметров определяется ГОСТом. Рассмотрим основные характеристики фильтровых анализаторов спектра, многие из которых в значительной степени могут быть применены и к другим типам анализаторов. Такими характеристиками являются:

диапазон частот;

разрешающая способность;

полоса обзора;

время анализа;

скорость анализа.

Диапазон частот анализатора спектра – это граничные значения частотного интервала, в котором возможен анализ спектра. Для расширения частотного диапазона, как уже известно, используется метод супергетеродинного приема. При необходимости диапазон частот может разбиваться на поддиапазоны.

Р азрешающая способность АС – это минимальный интервал по оси частот, при котором соседние составляющие спектра могут быть выделены как отдельные уровни и измерены их уровни. Реальная частотная характеристика фильтров анализатора спектра фильтрового типа изображена на рис. 8.6.

К(f)

Рис. 8.6. Частотная характеристика анализатора спектра

Как видно из рисунка, полное разделение соседних составляющих спектра всегда в какой-то мере условно, а при анализе сплошных спектров – невозможно. Поэтому мерой разрешающей способности АС считается значение Δfф. При этом различают статическую и динамическую разрешающие способности АС. Статическая разрешающая способность определяется только величиной Δfф и соответствует случаю, когда переходные процессы в фильтрах не искажают спектр. Динамическая разрешающая способность определяется не только Δfф, но и скоростью изменения частоты ГКЧ. При слишком большой скорости напряжение на выходе УПЧ не будет успевать изменяться в соответствии с изменением напряжения на входе, что приведет к появлению динамических искажений спектра.

Полоса обзора АС (ΔF) – это ширина изображения анализируемого спектра. Как уже указывалось раньше, для оценки спектра достаточно изображения одного основного лепестка и 2-3 боковых. Исходя из этого полоса обзора для типового прямоугольного радиоимпульса может быть определена по формуле:

ΔF = (6 – 8)/τи

Зная ширину полосы обзора для анализатора спектра параллельного типа можно определить необходимое число каналов фильтрации

n = ΔF/ Δfф

Время анализа для АС параллельного действия (Та) определяется как

Та пар.= 1/ Δfф + tс,

где tс – время, необходимое для съема показаний индикаторов.

Для АС последовательного действия

Та посл.= А/ Δfф ΔF / Δfф =А ΔF / Δf²ф,

где коэффициент А>1 – коэффициент, учитывающий динамическую разрешающую способность АС.

Скорость анализа (только для АС последовательного действия) – это скорость изменения частоты ГКЧ, а следовательно и скорость развертки осциллографического индикатора. Она может быть определена по формуле

V = ΔF/ Та пар.= Δf²ф/А.

Дисперсионный метод анализа спектра

Дисперсионный метод анализа спектра основан на использовании особенностей распространения радиосигналов в замедляющих системах с дисперсией фазовой скорости – дисперсионных линиях задержки. За счет дисперсии различные составляющие спектра будут задерживаться на различные интервалы времени и появляться на выходе линии задержки последовательно со сдвигом во времени. Если время задержки ДЛЗ линейно зависит от частоты, распределение энергии сигнала на выходе такой линии будет однозначно связано с ее частотой.

Структурная схема дисперсионного анализатора спектра изображена на рис. 8.6.

Как видно из рисунка, такая схема напоминает схему анализатора спектра последовательного действия с преобразованием частоты, только вместо детектора после УПЧ установлена дисперсионная линия задержки.

Рис. 8.6. Структурная схема дисперсионного анализатора спектра

Таким образом, в данной схеме входной сигнал до подачи на линию задержки подвергается линейной частотной модуляции. В этом случае на выходе ДЛЗ будет сформирован сигнал, соответствующий прямому преобразованию Фурье, причем время анализа будет минимизировано.

Достоинством такой схемы является ее высокое быстродействие и способность обрабатывать широкополосные сигналы (от десятков кГц до ГГц). Разрешающая способность схемы определяется конструкцией ДЛЗ (ультразвукового типа).

Рециркуляционный (интерференционный) метод анализа спектра

Метод основан на использовании гребенчатого фильтра ГФ с переменными параметрами (ГФПП). Структурная схема такого фильтра изображена на рис. 8.7.

Рис. 8.7. Структурная схема гребенчатого фильтра

Работает такая схема следующим образом. Пусть частота входного сигнала

ω_к = ,

где Т – время задержки в ЛЗ; К – целое число.

Тогда напряжение входного сигнала и напряжение обратной связи, снимаемое с линии задержки, совпадают по фазе и складываются в сумматоре. Причем совпадения будут повторяться периодически с периодом 2𝜋. Частотная характеристика такого фильтра имеет вид, представленный на рис. 8.8. Как видно из рисунка, такая ЧХ напоминает гребенку.

Рис. 8.8. Частотная характеристика ГФПП

Цифровой метод анализа спектра

Сущность цифрового метода анализа спектра состоит в преобразовании исследуемого сигнала в цифровой код и вычислении составляющих спектра с помощ0ью цифровых вычислительных устройств. Преобразование представляет собой дискретизацию сигнала во времени, квантование по уровню и цифровое кодирование. Все эти операции выполняются с помощью аналого-цифровых преобразователей (АЦП). Вычисление составляющих спектра дискретизированного сигнала основывается на использовании дискретного преобразования Фурье (ДПФ) и осуществляется с помощью специализированных микропроцессоров.

Алгоритм ДПФ заключается в следующем. Пусть исследуемый сигнал u(t) является непрерывной функцией времени и определен в интервале от 0 до Т (рис. ).

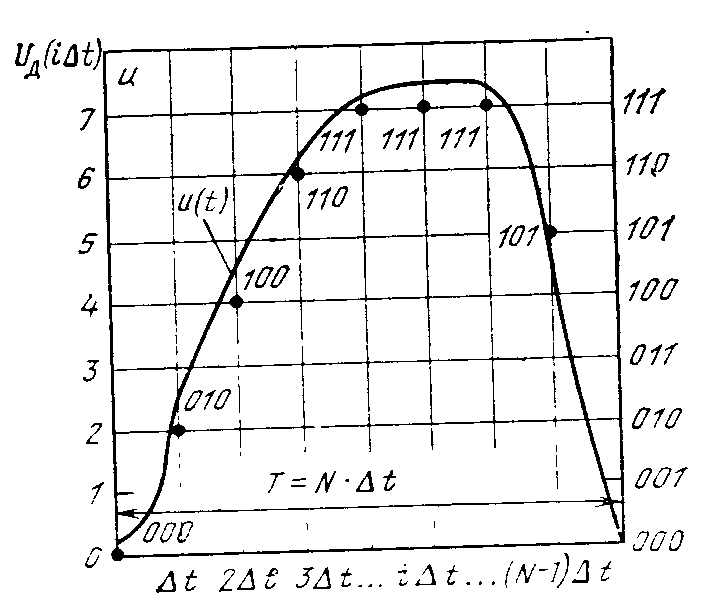
Рис.

Разобьем данный интервал на большое, но конечное число равных интервалов времени Δt и возьмем отсчеты значения сигнала через данные интервалы. Тогда комплексный спектр такого дискретного сигнала представится в виде ДПФ, аналитическая запись которого будет представлена в виде

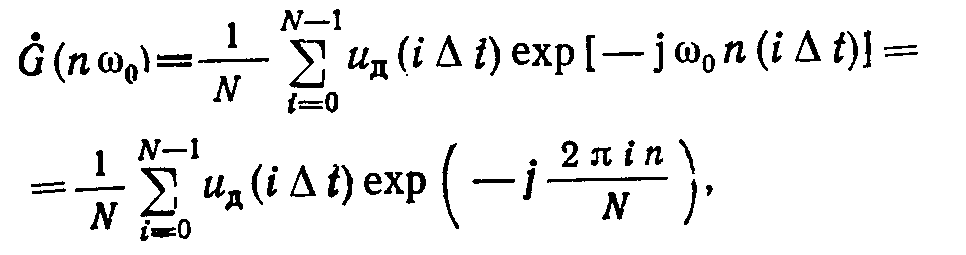
где u(iΔt) – значение i – го отсчета (i = 0,1,2, …, N-1); N – полное число отсчетов;

Т = NΔt; = 2π/T; n = 0,1,2, …, (N/2)-1 – номер спектральной составляющей;

G(n ω₀) – комплексные амплитуды исследуемого спектра.

Вычисление значений отсчетов реализуется на ЭВМ путем выполнения операций над действительными частями комплексных чисел. Полученный результат выводится на дисплей в виде спектральных линий (рис. ), амплитуда и частота которых соответствует спектру входного сигнала u(t).

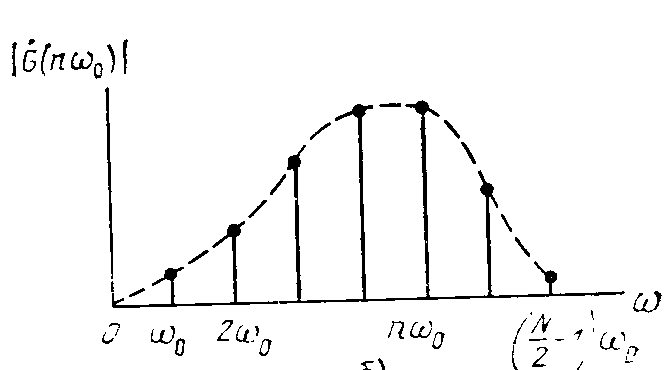
Рис.

На практике такой алгоритм обычно напрямую не производится, т.к. требует большого количества вычислений (обычно равное N²). Поэтому для вычислений используют цифровые фильтры (ЦФ) или быстрое преобразование Фурье (БПФ). ЦФ используются для анализа низкочастотных сигналов, а БПФ – высокочастотных сигналов.

ЦФ представляет собой электронное устройство со стабильной частотной характеристикой, не нуждается в подстройке, связанной со старением элементов. Его перестройка осуществляется методом перепрограммирования. С помощью ЦФ в анализаторах спектра реализуется процесс, называемый цифровой фильтрацией. Сущность цифровой фильтрации заключается в цифровом преобразовании последовательности числовых отсчетов входного сигнала в последовательность числовых отсчетов выходного сигнала. Если обозначить входной сигнал u_k, а выходной – y_k, то алгоритм работы цифрового фильтра будет выглядеть следующим образом

y_k = a₀u_k + a₁u_k-1 + a₂u_k-2 + … + a_mu_k-m.,

где a₀ ,a₁ ,a_2, …, a_m – постоянные весовые коэффициенты; m – порядок фильтра, т.е. максимальное число запоминаемых чисел.

С труктурная схема такого цифрового фильтра изображена на рис.

Рис.

На схеме Z^-1 - это элементы задержки входной последовательности на интервал дискретизации Z^-1 (задержка сигнала на интервал Δt в известном в математике z-преобразовании). Их еще называют ячейками памяти.

Блоки a_m – выполняют операцию умножения на соответствующие весовые коэффициенты. В совокупности с блоками задержки они образуют масштабные блоки.

Сигналы входной последовательности после задержки и умножения в масштабных блоках поступают на сумматор, на выходе которого образуется последовательность отсчетов выходного сигнала y_k.. Указанный выше ЦФ является нерекурсивным. Это значит, что его отклик на входной сигнал зависит только от значений входной последовательности. Существуют также и рекурсивные цифровые фильтры, которые имеют более сложную схему и отличаются от нерекурсивных тем, что при реализации вычислений используют кроме входных данных данные от ранее полученных результатов вычислений.

Быстрое преобразование Фурье представляет собой алгоритм, в основу которого положен принцип разбиения заданной последовательности отсчетов дискретного сигнала на ряд промежуточных подпоследовательностей. При этом входную последовательность представляют в виде двух подпоследовательностей с четными и нечетными номерами и половинным числом членов в каждой:

u_чт = u_2k; u_нч = u_2k-1; k = 0,1,2, … ,N/2 – 1

Коэффициенты Gn для четной и нечетной подпоследовательностей рассчитывают отдельно как Gnчт и Gnнч. Установлено, что коэффициенты Gn результирующего ДПФ входной последовательности в диапазоне номеров от 0 до N/2 – 1 определяются соотношением

Gn = Gnчт + Gnнч,

а коэффициенты входной последовательности для отсчетов с номерами от N/2 – 1 до N – 1

Gn = Gnчт - Gnнч,

Данные формулы представляют собой алгоритм БПФ. В них экспоненциальные фазовые множители учитывают влияние сдвига нечетной подпоследовательности относительно четной. Чтобы еще уменьшить количество вычислений четную и нечетную подпоследовательности разбивают на две промежуточные части и т.д. до получения простейших двухэлементных последовательностей. После выполнения вычислений четные и нечетные последовательности объединяют, используя их алгоритмы, подставляя в них значения n и N.

8.3. Измерение нелинейных искажений

Нелинейные искажения сигналов отрицательно сказываются на правильном функционировании радиоизмерительных устройств и на их метрологических характеристиках. Нелинейные искажения возникают в цепях, содержащих нелинейные элементы. Синусо­идальное напряжение, поданное на вход такой цепи, искажается, в результате чего форма выходного напряжения отличается от сину­соидальной.

Степень нелинейных искажений синусоидального напряжения характеризуется коэффициентом гармоник, определяемым как отношение среднеквадратического значения суммы всех высших гармоник напряжения, кроме первой, к среднеквадратическому значению напряжения первой гармоники:

Кг = = , (8.12)

Гармоники можно определить с помощью анализатора спектра, а затем вычислить коэффициент Кг по (8.12). Однако этот путь сложен. В основу работы прямопоказывающих измерителей нелинейных искажений положен принцип «подавления основной частоты». Принцип заключается в измерении отношения среднеквадратического значения напряжения высших гармоник к полному среднеквадратическому значению измеряемого сигнала. Аналитически это выглядит, как

К*г = / (8.13)

Сравнивая выражения (8.12) и (8.13) можно установить, что

Кг = = (8.14)

Если искажения невелики (Кг < 0,1), то коэффициенты Кг и К*г получаются меньше, чем на 1%. В соответствии с (15.13) для измерения коэффициента нелинейных искажений К*г необходимо измерить среднеквадратическое значение исследуемого сигнала и среднеквадратическое значение суммы высших гармоник (без первой). Схема измерителя нелинейных искажений представлена на рис. 8.11.

Рис. 8.11. Измеритель нелинейных искажений

Исследуемый сигнал поступает на входное устройство, содержащее разделительный конденсатор, чтобы развязать последующие цепи от постоянной составляющей сигнала и аттенюатор для изменения уровня входного сигнала. Устройство автоматической регулировки усиления АРУ предназначено для усиления и поддержания постоянного уровня сигнала на выходе при изменении входного напряжения. Таким образом, на режекторный усилитель, состоящий из усилителя и режекторного фильтра, поступает постоянное по уровню и точно известное напряжение исследуемого сигнала. Режекторный фильтр служит для подавления в исследуемом сигнале первой гармоники, остальные гармоники остаются при этом неизменными. В качестве режекторных фильтров применяются активные электрически перестраиваемые RC – фильтры.

После режекторного фильтра исследуемый сигнал без первой гармоники подается на широкополосный усилитель и с него – на преобразователь (может быть термоэлектрический преобразователь), обеспечивающий преобразование переменного напряжения в постоянное, пропорциональное среднеквадратическому значению переменного напряжения. В качестве индикаторного прибора может использоваться магнитоэлектрический вольтметр. Шкала прибора градуируется непосредственно в значениях Кг.

Примером такого измерителя нелинейных искажений может служить прибор С6-7, который измеряет коэффициент гармоник в пределах 0,05 – 30% в диапазоне частот 20Гц – 200кГц с основной погрешностью 0,1 Кг % + 0,1%.

Стремление повысить точность измерений и степень автоматизации привело к созданию цифровых измерителей нелинейных искажений. Примером такого измерителя нелинейных искажений может служить прибор С6-8, который измеряет коэффициент гармоник в пределах 0,03 – 30% в диапазоне частот 20Гц – 200кГц с основной погрешностью 0,06 Кг % + 0,003Кгм%, где Кгм – значение, соответствующее конечному значению шкалы.

При установке переключателя В в положение «Калибр» исследуемый сигнал u(t) с выхода усилителя подается непос­редственно на квадратичный электронный вольтметр, измеряю­щий среднеквадратическое значение исследуемого напряжения. При этом коэффициент усиления усилителя регулируется так, чтобы показания вольтметра были на предельном значении шкалы. Затем переключатель В переводится в положение «Изм.», заграждающий фильтр при этом настроен на частоту первой гармоники исследуемого сигнала. Вольтметр измеряет среднеквадратическое значение напряжения высших гармоник (кроме первой). Шкала вольтметра градуируется непосредственно в еди­ницах коэффициента — в процентах и децибелах; 1 дБ = = 20 lg (£7/0,775).

Рис. 15.6. Схема измерителя нелинейных искажений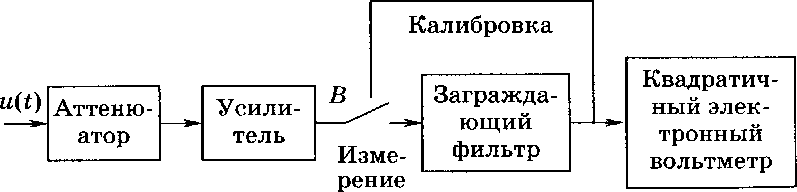

Так, измеритель нелинейных искажений предназначен для измерения коэффициента гармоник в пределах 0,1—30% иссле­дуемых сигналов в диапазоне частот 10 Гц—10 МГц. При боль­ших искажениях, когда Кт > 4—5%, нелинейные искажения можно обнаружить, наблюдая кривую исследуемого напряжения на экране электронного осциллографа.