5.5.2 Надстройка Поиск решения

 Надстройка Поиск решения используется для решения задач оптимизации. Для таких задач характерно обязательное наличие нескольких альтернативных решений и наличие некоторой оценочной функции для количественного выражения наилучшего выбора. Также задачи оптимизации могут иметь ограничения, формирующие множество допустимых альтернатив.

Задача оптимизации в общем виде включает следующие элементы:

• целевая функция – показывает, в каком смысле решение должно быть оптимальным. Возможны три вида целевой функции: максимизация, минимизация, назначение заданного значения.

• ограничения – устанавливают зависимости между переменными, могут быть односторонними и двусторонними, записанными в виде двух односторонних;

• граничные условия – показывают, в каких пределах могут быть значения искомых переменных в оптимальном решении.

Важная характеристика задачи оптимизации − ее размерность, которая определяется числом переменных n и числом ограничений m. Необходимым требованием является условие n>m. При n<m задачи решения не имеют. Систему уравнений, для которых n=m рассматривают как задачу оптимизации, имеющую одно допустимое решение. Ее можно решать как обычную задачу оптимизации, назначая в качестве целевой функции любую переменную.

Таким образом, задача имеет оптимальное решение, если она удовлетворяет двум требованиям: имеет более одного решения, т.е. существуют допустимые решения и имеется критерий, показывающий, в каком смысле принимаемое решение должно быть оптимальным, т. е. наилучшим из допустимых.

Надстройка Поиск решения позволяет найти оптимальное значение формулы, содержащейся в целевой ячейке. Чтобы получить по формуле, содержащейся в целевой ячейке, заданный результат, процедура изменяет значения во влияющих ячейках, представляющих решение задачи. Чтобы сузить множество значений, используемых в модели, применяются ограничения.

Типичной задачей оптимизации является транспортная задача, пример решения которой рассмотрим в следующем задании.

3. Используя надстройку Поиск решения, рассчитать оптимальный план перевозок бензина определенной марки между нефтеперерабатывающими заводами (НПЗ) и автозаправочными станциями (АЗС). Заданы:

1) объемы производства бензина (т):

НПЗ №1 – 10, НПЗ №2 – 14, НПЗ №3 – 17;

2) объемы потребления бензина (т):

АЗС №1 – 15, АЗС №2 – 12, АЗС №3 – 8.5, АЗС №4 – 5.5;

3) стоимость транспортировки 1 тонны бензина (усл. ед.) между НПЗ и АЗС (табл. 5.3).

Таблица 5.3

Стоимость транспортировки одной тонны бензина между НПЗ и АЗС, усл. ед.

	Пункты потребления	АЗС №1	АЗС №2	АЗС №3	АЗС №4
Пункты производства	НПЗ №1	3	5	7	11
	НПЗ №2	1	4	6	3
	НПЗ №3	5	8	12	7

Рекомендации по выполнению

• Постройте математическую модель задачи.

 Математической модель задачи оптимизации – специальная запись постановки и условий решения задачи оптимизации с использованием понятий математики и математической символики. Применительно к конкретной задаче оптимизации математическая модель соответствует математической постановке данной задачи.

Математическая постановка задачи: определить оптимальный план перевозок бензина от трех НПЗ для удовлетворения потребности четырех АЗС и минимизировать суммарные затраты на транспортировку. Целевой функцией назначить суммарные затраты на транспортировку бензина, ограничениями считать объемы производства бензина на каждом НПЗ и потребности в бензине на каждой АЗС.

• Создайте рабочую книгу Поиск решения и сохраните ее в папке Excel.

• Переименуйте Лист1, дав ему имя Транспортная задача.

• На листе Транспортная задача для решения задачи создайте таблицы и заполните их исходными данными, как показано на рис. 5.48.

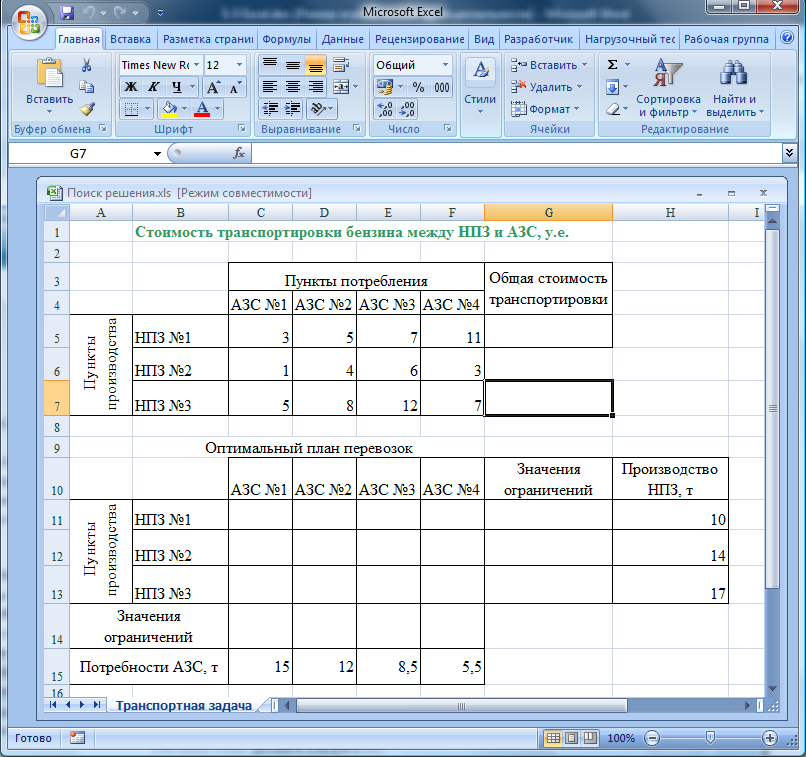
Рис. 5.48 Исходные таблицы для решения транспортной задачи

• Перейдите в режим отображения формул и задайте формулы в соответствии с математической постановкой задачи:

• сформируйте целевую функцию – в ячейку G5 введите формулу для расчета суммарных затрат на транспортировку бензина:

=СУММПРОИЗВ(C5:F7;C11:F13)

Данная формула рассчитывает сумму произведений стоимости перевозки от каждого НПЗ к каждой АЗС и соответствующих объемов перевозки.

• сформируйте ограничения – в ячейки G11:G13 введите формулы суммирования объемов перевозки с каждого НПЗ и в C14:F14 – формулы суммирования объемов перевозки к каждой АЗС (рис. 5.49).

 В табл. 5.4 представлены основные составляющие математической постановки задачи оптимизации с учетом исходных данных, приведенных в созданных таблицах.

Таблица 5.4

Составляющие математической постановки задачи оптимизации

Элемент	Описание
Целевая функция	Суммарные затраты на транспортировку бензина должны быть минимальными, т.е. G5 → min
Ограничения	1) Суммарные поставки бензина на одну АЗС должны равняться потребности в бензине на данной АЗС, т.е. C14=C15 D14= D15 E14=E15 F14=F15 2) Суммарные поставки бензина одним НПЗ должны быть равны количеству производимого бензина, т.е. G11 = H11 G12 = H12 G13= H13
Граничные условия	Значения искомых переменных в оптимальном решении должны быть только положительными, т.е.: С11:F13>=0

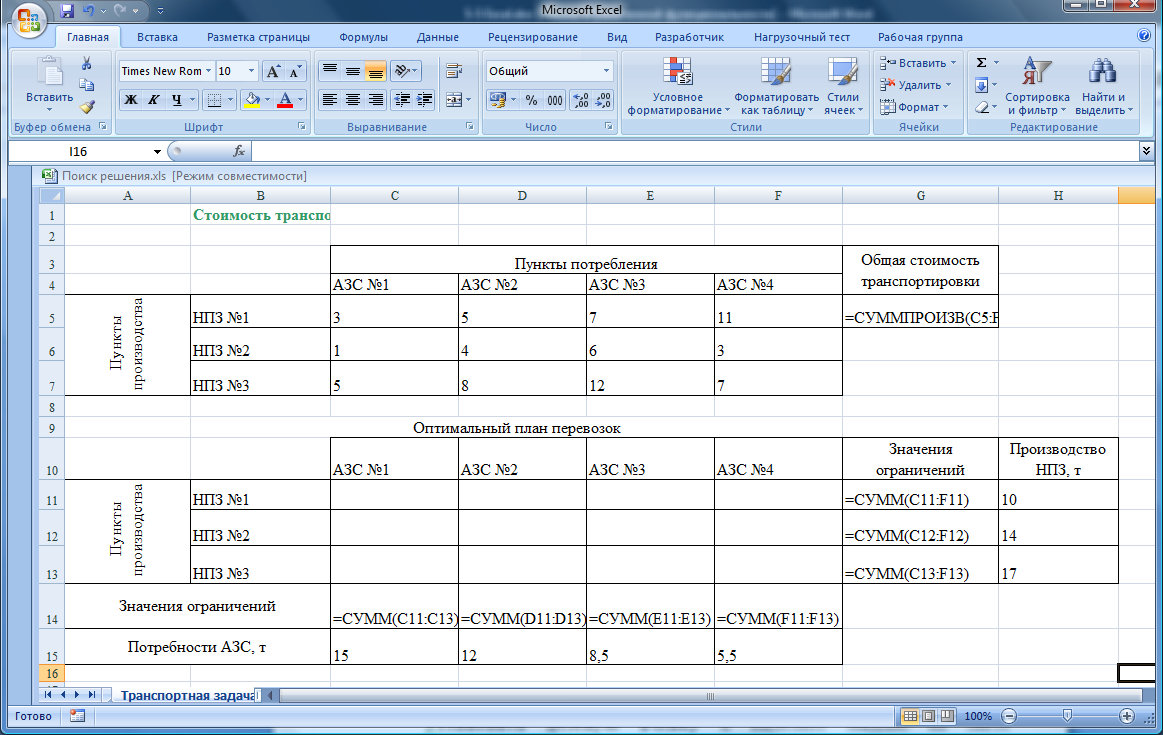
Рис. 5.49 Таблицы с формулами целевой функции и ограничений

• Откройте надстройку Поиск решения командой Сервис/Поиск решения.

• В окне Поиск решения (рис. 5.50) выполните следующее:

• укажите ячейку с целевой функцией – установите курсор в поле Установить целевую ячейку и выделите мышью на листе Транспортная задача ячейку G5;

Примечание. При выделении ячеек и диапазонов на рабочем листе в окне Поиск решения они автоматически преобразуются в абсолютные ссылки.

• укажите вид целевой функции – в группе Равной установите переключатель в положение минимальному значению;

• задайте диапазон влияющих ячеек, т.е. ячеек, которые должны изменяться в процессе поиска решения задачи, – в поле Изменяя ячейки укажите адрес диапазона ячеек $C$11:$F$13, выделяя его мышью на листе Транспортная задача.

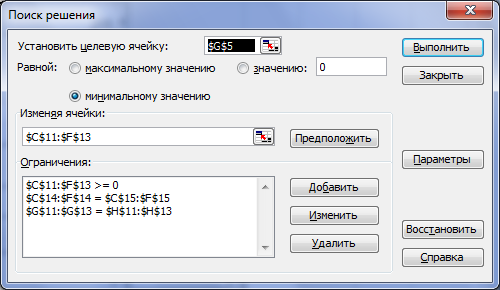
Рис. 5.50 Окно Поиск решения с заданными параметрами

• Добавьте ограничения, согласно математической постановке задачи (см. табл. 5.4). Для этого нажмите [Добавить] и открывшемся окне Добавление ограничения выполните следующее:

• для задания первого ограничения в поле Ссылка на ячейку укажите диапазон ячеек левой части неравенства – $C$14:$F$14 (диапазон выделяйте мышью на листе Транспортная задача); из раскрывающегося списка в центре окна выберите знак «=» (строгое равенство); в поле Ограничение укажите диапазон ячеек правой части неравенства – $C$15: $F$15 (рис. 5.51);

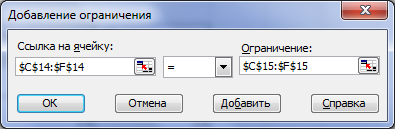
Рис. 5.51 Окно задания ограничения

• для добавления первого ограничения к параметрам поиска решения нажмите кнопку [Добавить], после чего оно появится в списке Ограничения окна Поиск решения (рис. 5.50);

• аналогично добавьте второе ограничение: $G$11:$G$13= $H$11:$H$13 и граничное условие: $С$11:$F$13>=0 и нажмите [ОК] в окне Добавление ограничения.

Примечание. Для изменения или удаления ограничений в окне Поиск решения используются соответственно кнопки [Изменить] и [Удалить].

• Щелкните на кнопке [Параметры], и установите в окне Параметры поиска решения флажок Линейная модель. Установка этого флажка позволит быстрее найти решение для линейной задачи.

• Запустите процесс вычисления оптимального плана нажатием кнопки [Выполнить] в окне Поиск решения. После завершения вычисления, найденные оптимальные значения будут вставлены в ячейки C11:F13 листа Транспортная задача (рис. 5.52).

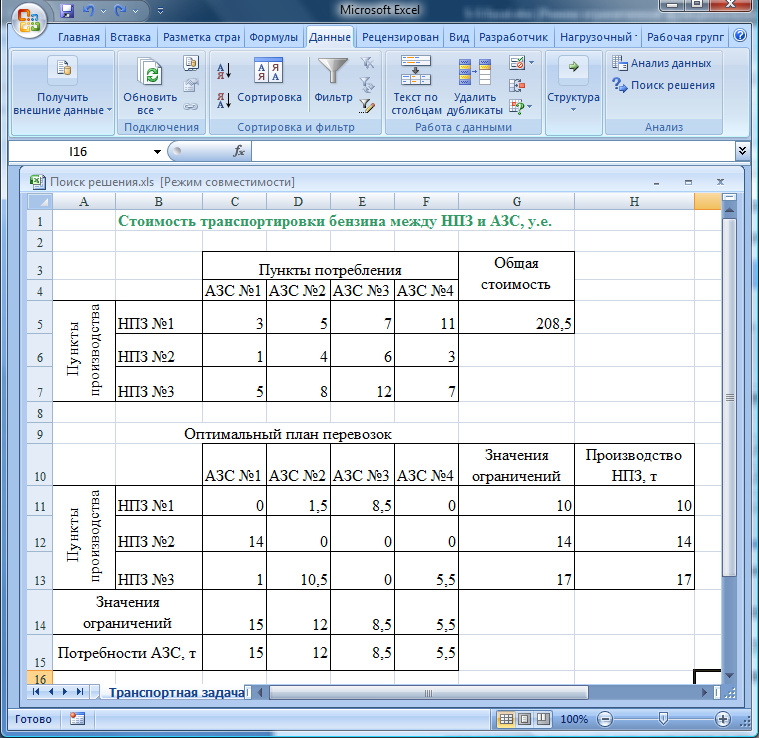
Рис. 5.52 Результат количественного решения транспортной задачи

• В открывшемся окне Результаты поиска решения (рис. 5.53) выберите:

• представление результатов в трех отчетах: Результаты, Устойчивость и Пределы;

• установите переключатель Сохранить найденное решение и нажмите [ОК].

Рис.5.53 Окно Результаты поиска решения

 Отчеты отобразятся на отдельных листах текущей книги с соответствующими именами:

Результаты  содержит целевую ячейку, список изменяемых ячеек и ограничений. Этот отчет также содержит информацию для каждого ограничения о таких параметрах, как состояние и разница;

Устойчивость  информирует, насколько целевая ячейка чувствительна к изменениям в ограничениях;

Пределы  сообщает, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи.

Результатом решения рассматриваемой задачи являются найденные оптимальные значения плана перевозок бензина (ячейки С11:F13). Найденному решению соответствует минимальное значение целевой функции – 208,5.

• Сохраните книгу Поиск решения.

4. Представить преподавателю результаты работы в папке Excel с файлами Пакет анализа и Поиск решения.

Задания для самостоятельной работы

1. Используя надстройку Пакет анализа, по данным задания 2, постройте прогнозы по методу скользящего среднего на интервалах данных в два месяца, а затем – в четыре месяца. Сравните прогнозы между собой и с фактическими данными.

2. Используя надстройку Поиск решения определить план выпуска продукции, обеспечивающий предприятию максимальную прибыль. Заданы:

1) на предприятии осуществляется выпуск четырех видов продукции А1, А2, А3, А4;

2) для выпуска продукции используют три вида сырья С1, С2, С3;

3) объемы выделенного сырья, нормы расходы сырья и прибыль на единицу продукции при изготовлении каждого вида продукции приведены в табл. 5.5.

Таблица 5.5

Нормы расхода сырья и прибыль от реализации единицы продукции

Виды сырья	Запасы сырья	Виды продукции
		А1	А2	А3	А4
С1	35	4	2	2	3
С2	31	1	1	2	3
С3	42	3	1	2	1
Прибыль		14	10	14	11

Контрольные вопросы

1. Каково назначение надстройки Пакет анализа?

2. Какие основные элементы управления содержат диалоговые окна инструментов для анализа данных?

3. Каково назначение надстройки Поиск решения?

4. Назовите этапы решения задач с помощью надстройки Поиск решения.

5. Что такое ограничения, как они задаются для решения задачи с помощью надстройки Поиска решения?

Индивидуальные задания

Примечание. Если при решении задачи нужно использовать ограничения на целочисленность значений, то в окне Параметры поиска решения следует нажать на кнопку [Параметры] и снять флажок Игнорировать целочисленные ограничения.

Используя надстройку Поиск решения решить задачу оптимизации нижеприведенных вариантов.

1. Определить сколько диванов каждого вида следует на фабрике ежедневно выпускать, чтобы прибыль от реализации была максимальной. Фабрика производит три вида диванов и использует для этого три вида ресурсов. Исходные данные приведены в таблице 5.6.

Таблица 5.6

Исходные данные для оптимизационной задачи варианта 1

Наименование ресурсов	Запас ресурсов, у.е.	Затраты ресурсов на производство диванов, у.е.
		1-й вид	2-й вид	3-й вид
Древесина, м2	700	2	1	5
Ткань, м	750	1	5	5
Фурнитура, шт.	700	5	3	1
Прибыль от реализации диванов, у.е.		115	110	100

2. Определить объем работ, который должны выполнить погрузчики на рабочих площадках, чтобы стоимость всех работ по погрузке была минимальной. Двум погрузчикам разной мощности не более чем за 24 часа нужно погрузить груз на двух площадках. Исходные данные приведены в таблице 5.7.

Таблица 5.7

Исходные данные для оптимизационной задачи варианта 2

Площадки	Объем груза, т	Производительность погрузчиков, т/ч		Стоимость работ, связанных с погрузкой одной тонны, у.е.
		1-й погрузчик	2-й погрузчик	1-й погрузчик	2-й погрузчик
Первая площадка	230	8	12	8	12
Вторая площадка	168	9	12	7	13

3. Определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной. Имеется 5 видов продуктов питания, в которых содержится 3 типа питательных веществ. Исходные данные представлены в таблице 5.8.

Таблица 5.8

Исходные данные для оптимизационной задачи варианта 3

Питательные вещества	Продукты питания, 1 кг					Суточная потребность в питательных веществах
	Хлеб	Мясо	Сыр	Бананы	Помидоры
Белки	61	220	230	15	11	150
Жиры	12	172	290	1	2	90
Углеводы	300	0	0	212	38	500
Калорийность продуктов	2060	1900	3600	890	230

4. Определить оптимальный объем выпуска красок каждого вида, обеспечивающий максимум общей стоимости готовой продукции. Производственное предприятие выпускает два вида краски – для внутренних и наружных работ, для производства которых используется три типа химических веществ. Исходные данные приводятся в таблице 5.9.

Таблица 5.9

Исходные данные для оптимизационной задачи варианта 4

Вещества для производства красок	Запасы веществ, кг	Расход веществ для производства красок, кг
		Для внутренних работ	Для наружных работ
Индиго	100	0,1	0,2
Железный купорос	70	0,2	0,1
Свежегашеная известь	55	0,15	0,05
Стоимость красок, руб.		25000	23000

5. Определить оптимальное количество издаваемых журналов каждой типографией, которое обеспечит максимально выручку от продажи. Издательский дом издает два журнала: "Механик" и "Автозапчасти", которые печатаются в трех типографиях. Исходные данные представлены в таблице в 5.10.

Таблица 5.10

Исходные данные для оптимизационной задачи варианта 5

Типография	Ресурс времени, отведенный типографией, ч	Время печати одной тысячи экземпляров журналов, ч
		«Механик»	«Автозапчасти»
А-пресс	112	2	14
В-принт	70	4	6
С-принт	80	6	4
Оптовая цена тысячи экземпляров, руб.		16000	12000
Спрос на журналы, тыс. шт.		12	7

6. Определить оптимальный план перевозок зерна, так чтобы все выращенное зерно было отправлено на склады, а суммарные затраты на транспортировку всего зерна были минимальными. Сельскохозяйственные кооперативы выращивают зерно. В качестве пунктов потребления выступают зерновые склады для хранения зерна. Исходные данные представлены в таблице 5.11.

Таблица 5.11

Исходные данные для оптимизационной задачи варианта 6

Кооперативы	Объем производства зерна, т	Стоимость транспортировки 1 т зерна между кооперативами и складами, у.е.
		Склад №1	Склад №2	Склад №3
Кооператив №1	200	90	60	110
Кооператив №2	300	90	80	130
Кооператив №3	140	70	85	100
Кооператив №4	360	160	115	100
Вместимость складов, т		350	250	400

7. Определить оптимальную партию часов каждого вида, которую может изготовить предприятие с целью получения максимальной прибыли. Некоторое предприятие выпускает два вида часов, для изготовления которых требуется два вида драгоценных металлов. Исходные данные приводятся в таблице 5.12.

Таблица 5.12

Исходные данные для оптимизационной задачи варианта 7

	Запасы драгоценных металлов, г	Расход драгоценных металлов, г
		Часы «Предприниматель»	Часы «Банкир»
Золото	1500	60	40
Платина	1800	20	60
Стоимость часов, у.е.		1500	2300

8. Определить, какое количество плит каждого типа можно изготовить в течение месяца так, чтобы обеспечить максимальную прибыль. Фирма выпускает два вида древесно-стружечных плит – обычные и улучшенные. Исходные данные представлены в таблице 5.13.

Таблица 5.13

Исходные данные для оптимизационной задачи варианта 8

Ресурсы	Запасы ресурсов на месяц	Затраты ресурсов на производство партии из 100 плит
		обычных	улучшенных
Материал, кг	4000	20	40
Время на прессование, ч	900	4	6
Время на отделку, ч	600	4	4
Цена партии, у.е.		30	50

9. Определить, какие и сколько наборов удобрений нужно купить, чтобы обеспечить эффективное питание почвы некоторого газона и минимизировать стоимость наборов. Фирма выпускает два набора удобрений для газонов. В наборы входят три вида удобрений. Исходные данные представлены в таблице 5.14.

Таблица 5.14

Исходные данные для оптимизационной задачи варианта 9

Удобрения	Требуемое количество удобрений для газона, кг	Содержание удобрений в наборах, кг
		обычный	улучшенный
Азотные	10	3	5
Фосфорные	20	4	8
Калийные	7	1	3
Цена наборов (у.е.)		4	7

10. Определить план выпуска изделий, который позволит заводу получить максимальную прибыль. Для изготовления изделий типа А1 и А2 склад может выделить не более 80 кг металла. Деталей типа А1 завод может изготовить за сутки не более 30 штук, типа А2 – не более 40 штук. Стоимость одного изделия типа А1 составляет 3 у. е., а типа A2 – 5 у. е. На изготовление одного изделия типа А1 идет 2 кг металла, типа А2 – 1 кг.

11. Определить количество продукции каждого вида, которое можно произвести при имеющихся запасах ресурсов с целью получения максимальной прибыли. Некоторое малое предприятие планирует выпуск двух видов продукции А и Б. Продукции вида А необходимо произвести не менее 10 единиц, а продукции вида Б можно не более 30 единиц. Остальные исходные данные представлены в таблице 5.15.

Таблица 5.15

Исходные данные для оптимизационной задачи варианта 11

Наименование ресурса	Запас ресурса	Цена единицы ресурса, у.е.	Нормы расхода ресурса на производство продукции каждого вида
			А	Б
Сырье С1, кг	190	20	5	8
Сырье С2, кг	200	30	10	5
Станки, машинодень	904	20	30	20
Трудовые ресурсы, человеко-день	4520	10	150	200
Прибыль от реализации единицы продукции, у.е.			220	330

12. Определить, сколько изделий каждой модели следует фирме выпускать в неделю, чтобы максимизировать прибыль. Фирма производит две модели А и В книжных полок. Для каждого изделия модели А требуется 3м² досок, а для изделия модели В – 4м², фирма же может получать от своих поставщиков до 1700м² досок в неделю. Для каждого изделия модели А требуется 12 минут работы оборудования, а для изделия модели В – 30 минут, всего неделю можно использовать до 160 часов работы оборудования. Изделие А приносит 2 у.е. прибыли, а изделие В – 4 у.е.

13. Определить, сколько столов различного типа следует выпускать фирме в неделю, чтобы максимизировать прибыль. Фирма производит 3 типа столов для кабинетов. Прибыль от продажи составляет: за стол 1-го типа – 15 у.е., за стол 2-го типа – 22 у.е., за стол 3-го типа – 19 у.е. Остальные исходные данные представлены в таблице 5.16.

Таблица 5.16

Исходные данные для оптимизационной задачи варианта 13

Работы по производству столов	Объем работ для производства столов, ч			Лимит объема работ в неделю, ч
	1-го типа	2-го типа	3-го типа
Изготовление частей	2	3	2	360
Сборка	1	2	3	240
Полировка	1	1	2	180

14. Определить оптимальное распределение времени на рекламу, обеспечивающее максимальный объем сбыта. Фирма имеет возможность рекламировать свою продукцию, используя местные радио и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены суммой 1000 у.е. в месяц. Каждая минута радиорекламы обходится 5 у.е., а каждая минута телерекламы – 100 у.е. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем телевидение. Удельный объем сбыта, обеспеченный минутой телерекламы 25 товаров/мин., а удельный объем сбыта, обеспеченный минутой радиорекламы – 1 товар/мин.

15. Определить оптимальный объем производства изделий каждого вида, обеспечивающий максимальную прибыль. Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства каждого изделия ограничено значением 8 часов в сутки. Исходные данные приведены в таблице 5.17.

Таблица 5.17

Исходные данные для оптимизационной задачи варианта 15

Изделие	Время обработки одного изделия, мин.			Прибыль, у.е.
	Станок 1	Станок 2	Станок 3
I	10	6	8	2
II	5	20	15	3

101