Раздел 3. Динамика раздел механики, в котором изучается движение материальных тел в пространстве в зависимости от действующих на них сил.
1. Динамика точки
Задача
6.
В железнодорожных
скальных выемках для защиты кюветов от
попадания в них с откосов каменных
осыпей устраивается «полка» DC.
Учитывая возможность движения камня
из наивысшей точки А
откоса и полагая при этом его начальную
скорость
,
определить наименьшую ширину полки b
и скорость
,
с которой камень падает на нее. По
участку АВ
откоса, составляющему угол α
с горизонтом и имеющему длину l,
камень движется τ
с. Коэффициент
трения скольжения f
камня на участке АВ
считать постоянным, а сопротивлением
воздуха пренебречь.
Дано:
.
Определить b
и
(рис. 10.3).
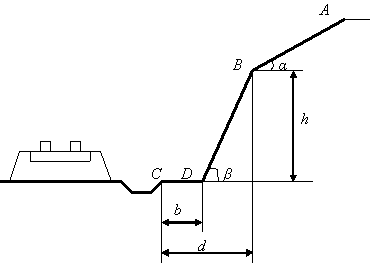
Рис. 10.3
Решение. Задачу разделим на два этапа. Первый – движение камня на участке АВ, второй – движение камня от точки В до С.
Первый
этап. 1. Составление расчетной схемы.
Ось
проводим по направлению движения камня,
ось
- перпендикулярно к оси
.
Камень принимаем за материальную точку
и показываем ее в текущем положении,
изображаем действующие на камень (точку)
силы: вес
,
нормальную реакцию
и силу трения скольжения
(рис. 10.4).
2.Выявление начальных условий.
При
.
Рис. 10.4
3.Составление дифференциальных уравнений движения точки. Так как точка (камень) движется прямолинейно, то при направлении оси х вдоль траектории получим одно дифференциальное уравнение движения
;
сила трения
,
тогда
;
;
.
4.Интегрирование дифференциальных уравнений движения. Интегрируя дифференциальное уравнение дважды, получаем:
;
;
;
;
;
;
.
5.Определение
постоянных интегрирования. Подставим
начальные условия, т.е.
в уравнения:
;
;
.
6.Нахождение неизвестных величин и исследование полученных результатов. После подстановки постоянных интегрирования С1 и С2 получаем уравнение скорости и уравнение движения:
;
.
Для момента времени τ, когда камень покидает участок АВ,
,
т.е.
;
.
Умножим первое уравнение на τ/2, после этого разделим его на второе. В результате получим:
;
;
.
Второй этап. Движение камня от точки В до точки С.
1.Составление расчетной схемы. Координатные оси покажем так, как это удобно для решения задачи, в нашем случае ось х параллельна горизонтали и проходит через точку В, ось у направляем вниз через точку В. Камень принимаем за материальную точку, показываем ее в текущем положении, изображаем действующую на камень силу тяжести (рис. 10.4).
2.
Выявление начальных условий движения.
При
:
.
3.Составление дифференциальных уравнений движения. Так как движение точки происходит в плоскости ху, то число уравнений движения равно двум:
.
4.Интегрирование дифференциальных уравнений движения. Интегрируем дифференциальные уравнения дважды:
(a)
;
(б)
(в)
.
(г)
5.
Определение постоянных интегрирования.
Подставляем начальные условия:
в уравнения (а – г):
,
откуда
.
6.Нахождение искомых величин и исследование полученных результатов. После подстановки постоянных интегрирования в уравнения (а –г) получаем следующие уравнения проекций скорости камня:
и уравнения его движения
.
Уравнение траектории камня найдем, исключив параметр t из уравнений движения:
;
– уравнение
параболы.
В
момент падения
.
Определим d
из уравнения траектории:
;
;
.
Так как траекторией движения камня является ветвь параболы с положительными абсциссами ее точек, то d=2,11 м.
Минимальная ширина полки
.
Используя
уравнение движения камня
,
найдем время Т
движения камня от точки В
до точки С
.
Скорость камня при падении найдем через проекции скорости на оси координат:
по формуле
.
Для момента падения t=T=0,53 c
.
Скорость камня при падении равна 12,8 м/с.