36. Теорема об изменении кинетической энергии в дифференциальной и интегральной форме.

Теорема об изменении кинетической энергии м.т.: дифференциал кинетической энергии мат точки равен элементарной работе действующей на точку силы. Т-Т₀=∑A(F_k) –производная в окончательной форме.

Производная от кинетической энергии точки по времени равна мощности действующей на точку силы.

Теорема об изменении кинетической энергии мех системы:T-T₀=∑A_k^e+∑A_kⁱ

37. Силовое поле. Потенциальное силовое поле. Работа сил потенциального поля. Две задачи в теории потенциальных силовых полей.

Силовым полем называется такая область пространства в которой на точку системы находящиеся в этой области действующие силы зависящие от положения точки или положения точки и независящие от скорости. Силовое поле силы которого не зависят от времени наз стационарным. Стационарное силовое поле наз потенциальным если работа силы поля на точку не зависит от траектории движения точки а определяется лишь начальным и конечным положением. Силы потенциальных силовых полей наз потенциальными или консервативными.

Работа силы поля равна разности работ или потенциальной энергии по переносу почки из нулевого положения в заданное. А=П₀-П₁

Две задачи в теории потенциальных силовых полей:1) по известной силовой ф-ции определить силу поля. Задача решается с помощью формулы

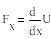
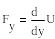
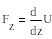
2 )По известной силе определить силовую ф-цию.

интергируем

38. Потенциальная энергия точки и механической системы.

Потенциальная энергия равна взятой с обратным знаком силовой ф-ции.

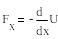
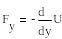
Потенциальной энергией системы (x, y, z) = (x₁, y₁, z₁, x₂, y₂, z₂, …, x_n, y_n, z_n) называется сумма работ сил потенциального поля, действующих на точки системы при ее перемещении из данного положения в нулевое.

Силовое поле F(x, y, z) будет потенциальным, если его можно представить в виде градиента скалярного поля:

F(x, y, z) = – grad  = – [(d/dx)i + [(d/dy)j + [(d/dz)k], где (x, y, z) – потенциальная энергия системы.

39. Полная механическая энергия. Закон сохранения механической энергии.

При действии на систему потенциальных сил сумма кинетической и потенциальной энергий остается постоянной в процессе движения. Т+П=const . Доказательство. Теорема об изменении кинетической энергии системы: T₂ – T₁ = A₁₂

для потенциального поля сил примет вид: T₂ – T₁ = ₁ – ₂, или T₁ + ₁ = T₂ + _{2… чтд}

При наличии трения полная механическая энергия изменяется и часть ее переходит в др. виды энергии(тепловую, электрическую, и др.).

40. Количество движения, момент количества движения и кинетическая энергия твердого тела.

Количество движения системы равно произведению массы всей системы на скорость ее центра масс. Кинетическая энергия твердого тела равна кинетической энергии поступательного движения со скоростью центра масс, сложенного с кинетической энергией вращательного движения вокруг оси, проходящей через центр масс. Т=(Мv²_c)/2+(_Jc ω²)/2