18. Теорема Гюйгенса-Штейнера о вычислении моментов относительно параллельных осей.

Момент инерции твёрдого тела относительно оси не проходящей через центр масс равен сумме моментов инерции относительно центральной оси проходящей через центр масс и параллельной заданной и произведение массы тела на квадрат расстояния между осями.

где

JC — известный момент инерции относительно оси, проходящей через центр масс тела,

J — искомый момент инерции относительно параллельной оси,

m — масса тела,

d — расстояние между указанными осями.

19.Вычисление моментов инерции однородных тел : тонкая пластина , тонкий стержень , кольцо, цилиндр, конус .

Тонкий стержень: 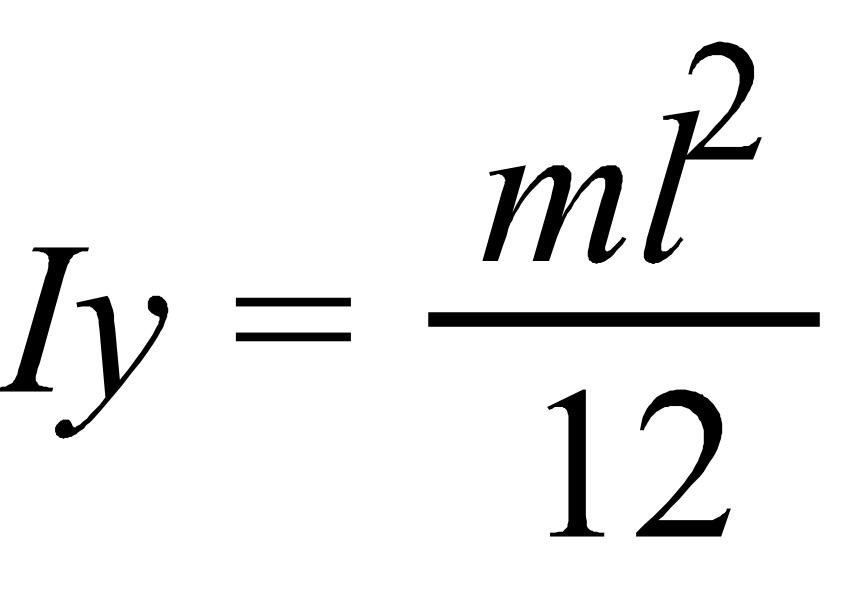Тонкий цилиндр :

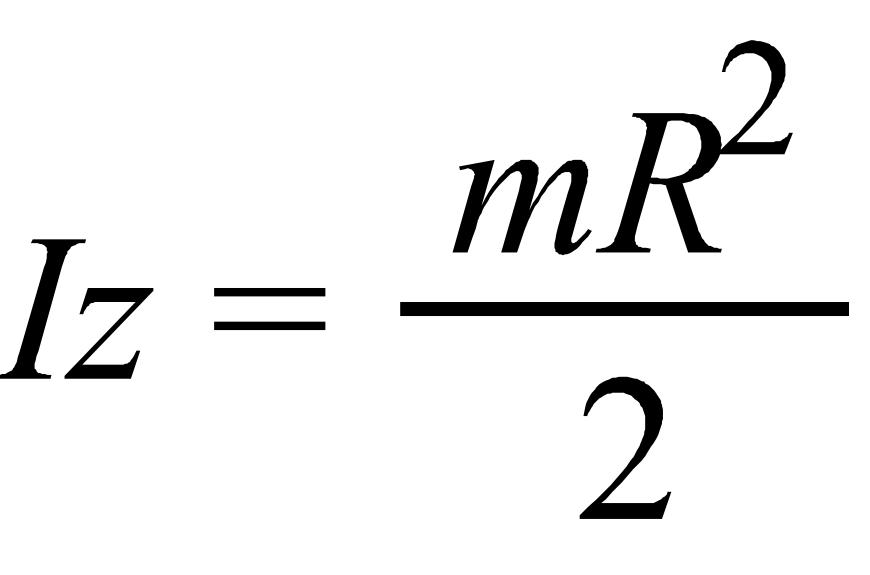
Тонкая пластина: Конус:

Тонкое кольцо: Шар:

20. Вычисление моментов инерции относительно произвольных осей.

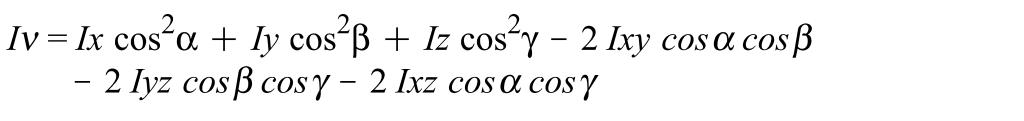Позволяет найти момент инерции относительно любой оси проходящей через оси координат и составляющие угля

с этими осями , через величины осевых и центробежных моментов инерции этих осей.

21. Эллипсоид инерции. Центральные оси инерции. Экстремальные свойства моментов инерции.

Центр эллипсоида находится в начале координат .

3 оси симметрии эллипсоида называются главными осями инерции , моменты инерции относительно главных осей называются главными моментами инерции.

Если в качестве осей координат принять главные оси инерции , то центробежные моменты инерции относительно этих осей будут равны нулю.

ЭЛЛИПСОИД ИНЕРЦИИ -поверхность, характеризующая распределение моментов инерции тела относительно пучка осей, проходящих через фиксированную точку О. Строится Э. и. как геом. место концов отрезков OK= 1/ , отложенных вдоль Ol от точки О, где Ol- любая ось, проходящая через точку О; Il - момент инерции тела относительно этой оси (рис.). Центр Э. и. совпадает с точкой О, а его ур-ние в произвольно проведённых координатных осях Oxyz имеет вид

где Ix, Iy, Iz - осевые, а Ixу, Iyz, Lzx - центробежные моменты инерции тела относительно указанных координатных осей. В свою очередь, зная Э. и. для точки О, можно найти момент инерции относительно любой оси Оl, проходящей через эту точку, из равенства Il= 1/R2, измерив в соот-ветдтвующих единицах расстояние R = OK.

22. Дифференциальные уравнения движения точек механической системы.

Рассмотрим механическую систему, состоящую из n материальных точек M_i c массами m_i (i = 1, 2, …, n), на каждую из которых действует равнодействующая внешних F_i^(e) и внутренних F_i⁽ⁱ⁾ сил.

Для каждой точки системы можно записать основное уравнение динамики:

m_ia_i = F_i^(e) + F_i⁽ⁱ⁾ , (i = 1, 2, …, n). (3.4)

Проектируя каждое из уравнений (3.4) на оси координат, получим систему 3n дифференциальных уравнений второго порядка, описывающих движение системы

(3.5)

(i = 1, 2, …, n). Эти уравнения и называются дифференциальными уравнениями движения системы. Вместе с соответствующими начальными условиями они образуют задачу Коши, решив которую, мы найдем закон движения механической системы.

О том, насколько сложной является поставленная задача можно судить хотя бы по тому, что к настоящему времени в общем виде она решена только для n = 2.