46. Приближенная теории гироскопов. Гироскоп с двумя, тремя степенями свободы. Гироскопический эффект, гироскопический момент.

Гироскоп – твёрдое тело, имеющее одну неподвижную точку и совершающее движение вокруг этой точки с большой угловой скоростью. Если центр тяжести гироскопа совпадает с неподвижной точкой, гироскоп называется астатическим. В любом другом случае - тяжёлым. В общем случае гироскоп имеет три степени свободы. Если угол нутации не меняется, то гироскоп имеет две степени свободы. Гироскоп с двумя степенями свободы участвует одновременно в двух движениях: в собственном вращении с угловой скоростью; и прецессионном. При расчётах с использованием приближённой теории используется теорема Резаля.

U= =M₀^e

У гироскопа с тремя степенями свободы все три угла Эйлера изменяются в процессе движения. Поэтому его движение ограничивается только одной неподвижной точкой О.

М₀ вызывает действие на опоры в точках А и В дополнительного момента М_r= - М₀^r – гироскопического момента. Наличие гироскопического момента называется гироскопическим эффектом.

47. Принцип Даламбера для механической системы. Главный вектор и главный момент сил инерции в различных случаях движения твердого тела.

При движении механической системы главный вектор и главный момент внешних сил относительно произвольного центра как бы устанавливается главным вектором и главным моментом относительно того же центра сил инерции.

∑F_k^e+R^u=0

∑M₀(F_k^e)+M₀^u=0

Главный вектор и главный момент сил инерции в различных случаях движения твердого тела:

Поступательное движение

R^u=-M*a_c M_z^u=0

Вращение тела вокруг оси не проходящей через центр масс.

R^u=-M*a_c M_z^u=-I_z*ε

Вращение вокруг оси проходящей через центр масс.

R^u=0 M_z^u=-I_z*ε

Качение.

R^u=-M*a_c= Фщ M_z^u=-I_z*ε ε= a_c/R

48. Определение динамических реакций подшипников при вращательном движении твердого тела.

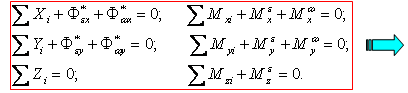
49. Связи и их классификация.

Механическая система называется свободной если её положение или движение не ограничено другими телами не входящими в эту систему (связями).

Связи конструктивно реализуются в виде шарниров, стержней, нитей и т.д. и может описываться в виде уравнений и неравенств.

Виды связи:

Геометрические – связи ограничивающие только координаты точек механической системы

f(x,y,z)=0

Дифференциальные – связи оказывающие ограничения на координаты или скорости системы

f(x,y,z, )=0

Голономные – все геометрические связи и те дифференциальные, которые могут быть проинтегрированы.

Неголономные – дифференциальные неинтегрируемые связи.

Стационарные – связи характеризующие свое действие в течении времени.

f(x,y,z)=0

Нестационарные – связи действие которых на тело меняется с течением времени.

f(x,y,z,t)=a

Удерживающие – связи ограничивающие положение точки в двух взаимно перпендикулярных направлениях.

Неудерживающие – связи ограничивающие положение точки в одном направлении и допускают ее перемещение в противоположном.