1.Законы динамики. Основное уравнение динамики точки.

1-й закон динамики (закон инерции): всякое , изолированное от внешних воздействий тело , сохраняет состояние покоя или равномерного прямолинейного движения до тех пор , пока воздействие со стороны других тел не выведут его из этого состояния.

2-й закон динамики (основной): ускорение , сообщаемое м.т. силой , прямопропорционально величине этой силы и совпадает с ней по направлению. F=ma a=F/m

3-й закон динамики (закон взаимодействия): силы взаимодействия между собой двух тел равны по модулю и направлены по одной прямой в противоположные стороны. F12=-F21

4-й закон динамики (принцип независимости действия сил): ускорение сообщаемое м.т. равнодействующей силой равно геометрической сумме ускорений , которые получила бы точка от действия каждой из сил по отдельности.

2. 1-я и 2-я основные задачи динамики и методы их решения.

1-я задача (прямая): по известной массе точки и кинематическим характеристикам движения определяется действующая сила (решается дифференцированием кинематического уравнения движения)

2-я задача (обратная): по известным , массе точки , действующим силам и начальным условиям движения определить кинематические характеристики (решается интегрированием ДУ движения)

3. Принцип Даламбера для материальной точки. Примеры.

Принцип Даламбера устанавливает единый подход к исследованию движения любой механической системы вне зависимости от характера налагаемых на это движение условий. При этом динамическим дифференциальным уравнениям движения придается вид уравнений равновесия. Рассмотрим несвободную материальную точку М, движущуюся по кривой АВ под действием активных сил, равнодействующая которых равна F. Обозначив через N силу реакции, с которой кривая АВ действует на точку М, запишем основное уравнение динамики точки/ Силы F, N, Ф образуют сходящуюся систему сил и полученное уравнение выражает условие равновесия этой системы, что и составляет принцип Даламбера для материальной точки. В каждый момент движения материальной точки действующие на нее активные силы, силы реакций наложенных на точку связей и условно приложенная к точке сила инерции образуют уравновешенную систему сил. Прикладывая силу инерции к движущейся точке, мы можем говорить лишь об условном равновесии приложенных к ней сил. Однако такая трактовка динамического уравнения движения в некоторых случаях обеспечивает наиболее простое и удобное решение задач динамики - (особенно первой), и поэтому принцип Даламбера широко применяется во многих прикладных дисциплинах.

П ри движении материальной точки векторная сумма действующих на ней активных сил , равнодействующих реакций и сила инерции будет равна нулю.

Сила инерции равна произведению массы тела на его ускорение и направлена противоположно ускорению. Ф=-ma

4. Дифференциальные уравнения движения точки в декартовых и естественных осях координат. Дифференциальные уравнения движения несвободной материальной точки в форме Эйлера.

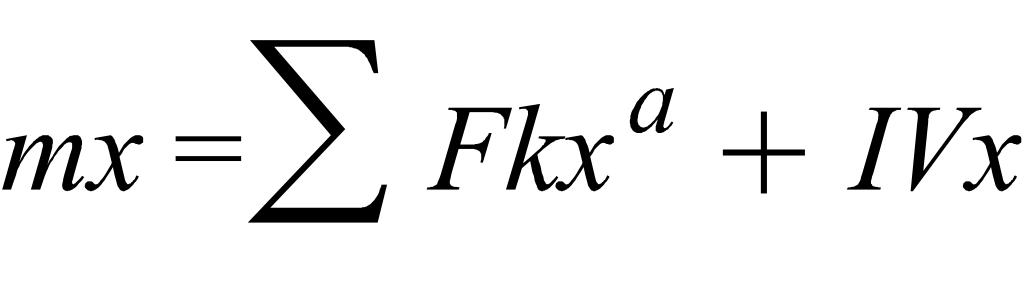
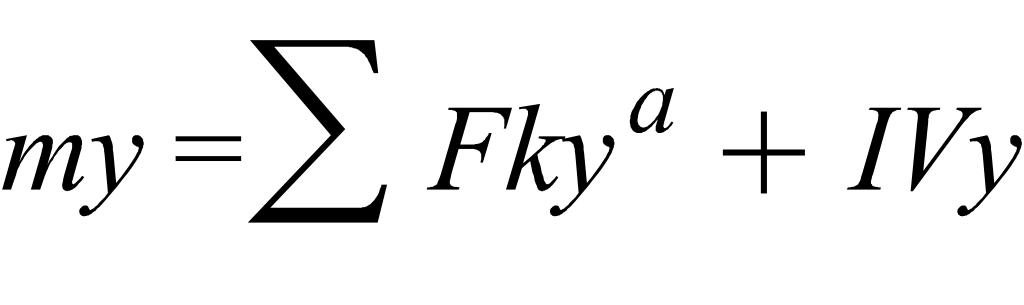- ДУ движения несвободной м.т. в декартовых координатах

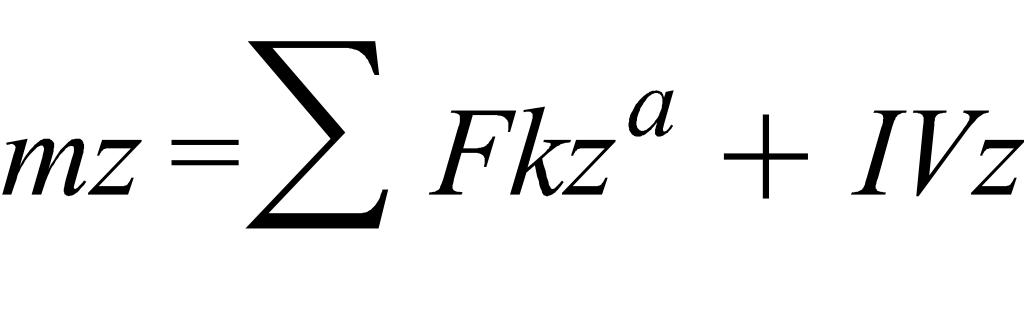
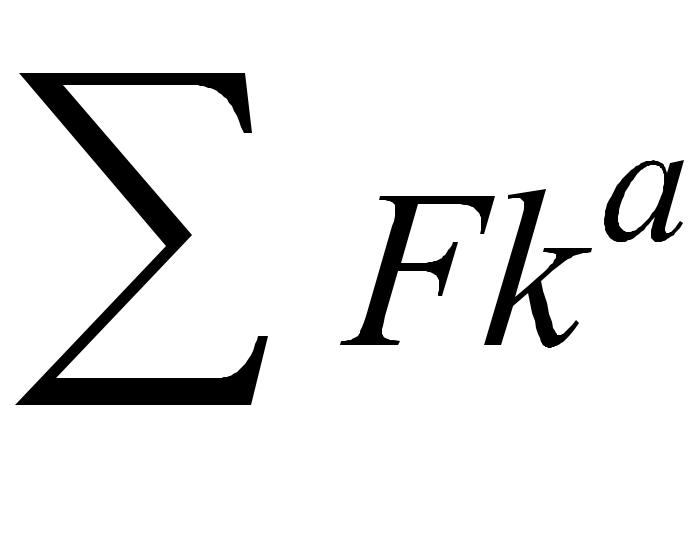- главный вектор (геом. Сумма действующих на точку активных сил)

Если точка является несвободной (на движение точки наложены связи), в число действующих на точку сил включаются реакции связей.

Силы, входящие в правую часть дифференциальных уравнений движения, в общем случае могут являться функциями от времени t, скорости v и координат х, у, z точки.

- равнодействующая реакция связи

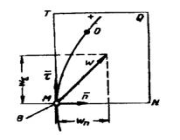
Дифференциальные уравнения в естественных координатах. Проектируя основное уравнение динамики на оси естественной системы координат, получим: