3.4.4 Моделирование реактора полного вытеснения

Адиабатический режим

Задаем параметры входящего потока

Рассчитаем плотность потока при температуре входного потока, используя метод аппроксимации (приведен в пункте 3.4.3)

_кг/м³

Объемный расход потока (м³/с)

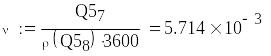
Мольные расходы компонентов (кмоль/с)

Молярные концентрации компонентов во входящем потоке (кмоль/м³)

Теплоемкости, кинетические и термодинамические параметры компонентов входящей смеси такие же, как и для расчета реактора идеального смешения (см. 3.4.3)

Математическая модель реактора полного вытеснения

Задаем начальное приближение

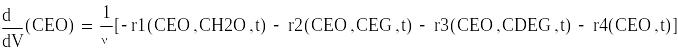
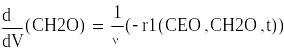
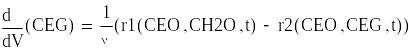
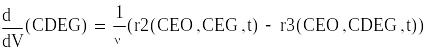
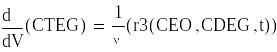
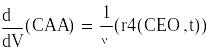
Запишем вектор, определяющий начальные параметры входного потока.

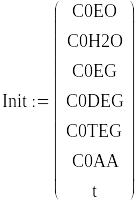
Заменим конечные концентрации выходного потока с использованием переменной Y для возможности определения оптимального объема реактора, для достижения степени конверсии этилен оксида равной 98%.

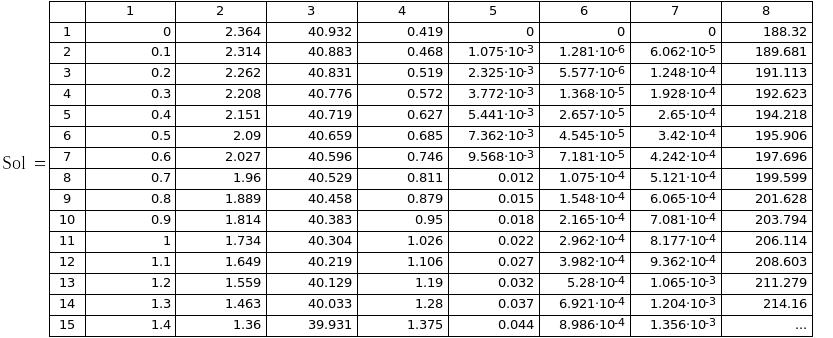
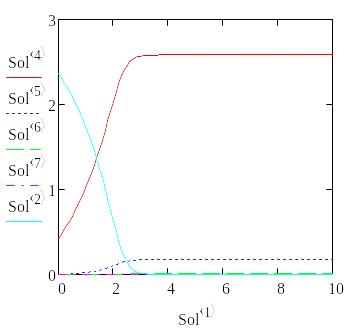
Решение системы сводим в таблицу и строим графики зависимости концентраций компонентов от изменения объема реактора.

Найдем оптимальный объем реактора

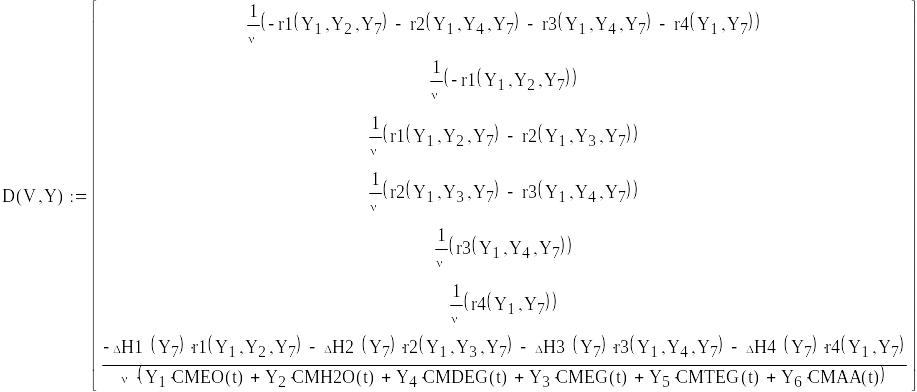
Рассчитаем выход продукта – этиленгликоля.

Изотермический режим

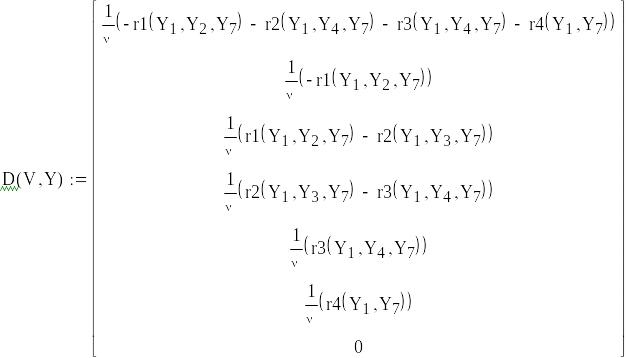
Рассчитаем выход продукта – этиленгликоля.

4. Оптимизация процесса производства гликолей с помощью полного факторного эксперимента 1 рода.

Влияющие факторы:

х1 – общий расход потока (кг/ч)

х2 – расход ЕО (кг/ч)

х3 – температура входного потока ºС

Задание факторов на базовом уровне

Интервалы варьирования влияющих факторов

Составим матрицу планирования в кодированной форме

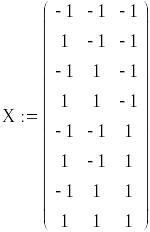
Составим матрицу планирования в размерной форме. Для перехода используем уравнения:

Матрица планирования в размерной форме

Функцией отклика является выход этиленгликоля (для её получения используем модель реактора полного вытеснения, разработанная ранее п. 3.4.4)

Проведем эксперимент (последовательно подставим значения влияющих факторов, на выходе получим функцию отклика, результаты запишем в виде вектора Y).

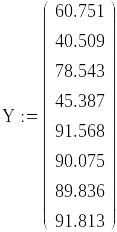
Получим расчетные данные, используя план первого порядка.

Уравнение регрессии имеет вид (ПФЭ).

Рассчитаем коэффициенты

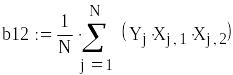
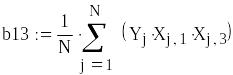
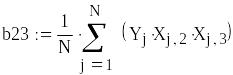
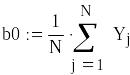
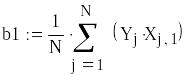
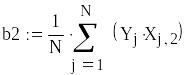
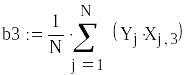
Получим функцию отклика, рассчитанную с помощью уравнения.

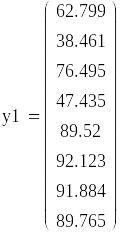
Рассчитаем относительную погрешность проведенного эксперимента

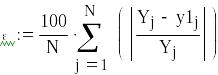
Рассчитаем коэффициенты в уравнении регрессии в размерной форме, используя уравнения: