11. Неоднородные линейные уравнения. Теоремы 1 и 2.
Неоднородным линейным уравнением называется уравнение вида
y”+p(x)y’+q(x)y=
(x)
(1)
Уравнению. (1) соответствует линейное однородное уравнение
Y”+p(x)y’+q(x)y=0 (2)
Т1.
Пусть
общее
решение уравнения (2),
Y=
– частное решение уравнения (1)
Тогда
y=
=
-
общее решения уравнения (1)
Доказательство: Запишем уравнение (1) в виде: L(y)= (x)
L(y)=левая
часть Находим L(
+
)=L(
)+L(
)=0=
(x)
То
есть
(3)
Определителем
системы относительно
Теорема доказана.
-
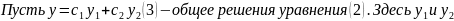линейно
независимые частичное решения уравнения
(2).
Будем искать решения уравнения
(1) в виде (3), где
m
1.
y’’+p(x)y’+q(x)y=
-
линейно
независимые частичное решения уравнения
(2).
Будем искать решения уравнения
(1) в виде (3), где
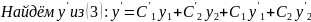
Объединяя
равенства (4) и (7)
Это
система линейных алгебраических
уравнений относительно
Определитель
системы (8)
Получим:
13. Метод неопределённых коэффициентов
Рассмотрим дифференциальное уравнение
(1)
где
-
константы,
функция специального вида.
Уравнению (1) соответствует однородное уравнение
,
Характеристическое уравнение которого
(2)
Рассмотрим
2 вида функции
1)
,
(3)
где
- многочлен степени
Если
не является корнем характеристического
уравнения (2), то частное решение уравнения
(1) ищем в виде
где
- (4)
многочлен степени
с неопределёнными коэффициентами. Если
простой
корень характеристического уравнения
(2), то частное решение уравнения (1) ищем
в виде
Если же двойной корень характеристического уравнения (2), то частное решение уравнения (1)ищем в виде
где
- многочлены степени соответственно
если
не является корнем характеристического
уравнения (2), то частное решение уравнения
(1) ищем в виде
(5)
где
- многочлены неопределёнными
коэффициентами степени
Если - корень характеристического уравнения (2), то частное решение уравнения (1) ищем в виде
Ряды Фурье
1. Ряды Фурье. Определение. Разложение периодической функции в ряд Фурье
Определение. Функциональный ряд вида
+
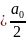(1)
называется рядом Фурье (или тригонометрическим рядом).
Постоянные
числа
называются
коэффициентами ряда Фурье.
Если
ряд (1) сходится, то его сумма есть
периодическая функция с периодом 2
Пусть
– периодическая функция с периодом
2
.
Предположим, что
разлагается в ряд Фурье, т.е.
.
(2)
едположим,
что ряд (1) для
мажорируемый и все действия, проводимые
ниже, законны.
Определение коэффициентов ряда Фурье.
Проинтегрируем обе части равенства
(2) в пределах от –
.
Так как
=
=0,
то
,
откуда следует
.
(3)
Для
вычисления остальных коэффициентов
рассмотрим предварительно интегралы.
Пусть
и
- целые числа и
.
Тогда
(4)
При
получим
(5)
Для
вычисления
умножим обе части равенства (2) на
,
а затем проинтегрируем полученное
равенство от
до
:
+
+
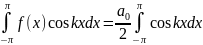(6)
Из равенств (4) и (5) следует, что все интегралы в правой части равенства (6) равны нулю, кроме интеграла с коэффициентом , т.е. при . Следовательно
,
откуда получим
.
(7)
Умножая
обе части равенства (2) на
и снова интегрируя от
до
,
получим
откуда
(8)
Коэффициенты, определенные по формулам
(3), (7) и (8), называются коэффициентами
Фурье для функции
а тригонометрический ряд (1) с такими
коэффициентами называется рядом Фурье
функции
Теорема. Если периодическая
функция
с периодом
кусочно-дифференцируемая на отрезке
,
то её ряд Фурье (2) сходится к
в каждой точке непрерывности и к
значению
в точках разрыва.
2. Ряды Фурье для четных и нечетных
функций. Пусть
- четная функция, тогда
.
Аналогично, если
– нечетная функция, то
.
Предположим теперь, что
- четная периодическая функция с периодом
,
тогда, очевидно,
- четная функция, а
– нечетная. Следовательно, коэффициенты
Фурье для такой функции будут
образом, ряд Фурье для четной периодической
с периодом
функции
будет иметь вид
- нечетная периодическая функция. Тогда
- нечетная функция,
– четная функция. Следовательно, для
нечетной периодической функции
с периодом
коэффициенты будут
и её ряд Фурье имеет вид
3. Ряды Фурье для функций с периодом
Пусть
- периодическая функция с периодом
,
т.е.
.
Разложим
в ряд Фурье. Для этого сделаем замену
переменной
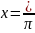(1)
будет периодической функцией по
с периодом
.
Действительно,
)=f(
Разложим функцию в ряд Фурье на отрезке
(2)
где
(3)
переменной
(1),
,
выражения (2) и (3) примут вид
,
,
,
.
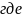
Рассмотрим случаи четной и нечетной периодической функции с периодом . Пусть - четная периодическая функция. Тогда её ряд Фурье будет иметь вид.
,
где
.
нечетной периодической функции
ряд Фурье имеет вид
,
где
.
Замечание.
Пусть функция
задана на отрезке
.
Дополним определение данной функции
произвольным образом на отрезке
так, чтобы выполнялись условия теоремы
о разложении функции в ряд Фурье. Тогда
мы можем разложить эту функцию в ряд
Фурье на отрезке
В частности, дополняя функцию
на
четным образом, получим ряд Фурье,
содержащий только косинусы. Если же
функцию
продолжить на
нечетным образом, то ряд Фурье такой
функции будет содержать только синусы.