Наслідок

Важливим наслідком формули Баєса є формула повної ймовірності події, що залежить від декількох несуміснних гіпотез (і тільки від них).

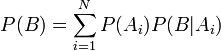 — ймовірність настання події B, що залежить від гіпотез  , якщо відомі їх ступені достовірності

17 Охарактеризувати схему Беруллі

Проводяться n дослідів, у кожному з яких може настати певна подія («успіх») з ймовірністю p (або не настати — «неуспіх» — q = 1 — p). Задача — знайти ймовірність отримати k успіхів у досліді.

Розв'язок:

Кількість успіхів — випадкова величина, що має розподіл Бернуллі.

Властивості

Нехай p — ймовірність успіху в схемі Бернуллі, q=1-p.Тоді найімовірнішою серед подій   є подія  , де   можна знайти з нерівності  .

18 охарактеризувати формулу Пуасона

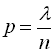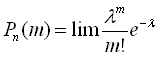Формула Пуассона дає приблизне значення імовірності   в тому випадку, коли число випробувань nвелике, а імовірність p=P(А) в кожному з окремих випробувань маленька, оскільки добуток цих чисел   є заданим числом, незалежним від n, а значить  , досить мале. Тоді  , m=0, 1, 2,…, n. Сума всіх ймовірностей дорівнює:

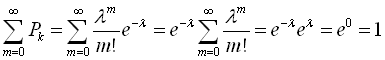
Значить  де  . Одержано формулу Пуассона або закон Пуассона. Цей закон дає можливість наближати біноміальний розподіл при великій кількості випробувань і малій імовірності події А в кожному випробуванні. 

19 Охарактеризувати локальну теорему Муавра Лапласса

Локальна теорема Муавра — Лапласа описує наближення нормального розподілу до біноміального розподілу. Є окремим випадком центральної граничної теореми.

Теорема

Якщо  , тоді для k в  -околі точки np, існує наближення^[1]

Гранична форма теореми стверджує, що

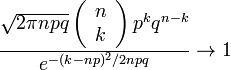
для 

Можливо, формулювання стає ясним не відразу, проте практичний зміст теореми простий: при великих значеннях n імовірність спостерігаючи рівно m успіхів можна приблизно розраховувати за формулою: 

20 Охарактеризувати випадкові величини та функції розподілу

Випадкова величина  є одним з основних понять теорії ймовірностей

Означення

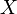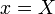• Випадковою величиною є будь-яка (не обов'язково числова) змінна  , "значення" якої   утворюють множину  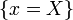 елементарних подій, або, іншими словами, позначають точки в просторі вибірок. Відповідний розподіл імовірностей називається розподілом випадкової величини  . ^[2]

Множина   елементарних подій являє собою можливі значення випадкової величини  , називається областю значень цієї величини . ^[3]

Властивості

Випадкова величина X — це вимірна функція, визначена на даному вимірному просторі  , тобто, вона визначається шляхом зіставлення кожної елементарної події з деякимдійсним числом. Більш формально:

 називається випадковою величиною, якщо  , де   --  -алгебра Борелевих множин на  .

Нехай x₁, x₂, … — значення випадкової величини X. Одне і те саме значення x_j може відповідати, взагалі кажучи, різним елементарним подіям. Множина усіх цих елементарних подій утворює складену випадкову подію, що полягає в тому, що X = x_j. Ймовірність цієї події позначається  . Система рівнянь:

визначає розподіл ймовірностей (слід відрізняти від функції розподілу ймовірностей) випадкової величини X.

Очевидно, що:

 та  .

Якщо дві або більше випадкових величини X₁, X₂, …, X_n визначено на одному просторі елементарних подій, то їх спільний розподіл задається системою рівнянь, в яких всім комбінаціям ,   і т. д. призначаються визначені ймовірності.

Випадкові величини називаються незалежними, якщо для довільної комбінації значень  ,  , …,   виконується рівність:

Тобто, якщо X_k залежить лише від k-го випробування, то випадкові величини X₁, X₂, …, X_n взаємно незалежні.

Ймовірність випадкової величини

• Ймовірність випадкової величини   дорівнює інтегралу ймовірностей взятому по її області значень: ^[4]

де

;   — граничні значення нормованої величини  ;

 — це середнє значення величини  ;

 — cтандартне відхилення цієї величини.

Функція розподілу ймовірностей — В теорії ймовірностей це функція, яка повністю описує розподіл ймовірностей випадкової величини.

Нехай   — ймовірнісний простір, в якому   — множина елементарних подій,   — сукупність підмножин  , що утворюють  -алгебру, множини з   називаються випадковими подіями,   — міра на  , що задовольняє умову  . Функція  , визначена   рівністю

,

називається функцією розподілу ймовірностей або кумулятивною функцією розподілу ймовірностей випадкової величини ξ. Вираз в правій частині рівності є ймовірністю того, що випадкова величина   набуває значень менших або рівних  .

Функція розподілу ймовірностей — В теорії ймовірностей це функція, яка повністю описує розподіл ймовірностей випадкової величини.

Нехай   — ймовірнісний простір, в якому   — множина елементарних подій,   — сукупність підмножин  , що утворюють  -алгебру, множини з   називаються випадковими подіями,   — міра на  , що задовольняє умову  . Функція  , визначена   рівністю

,

називається функцією розподілу ймовірностей або кумулятивною функцією розподілу ймовірностей випадкової величини ξ. Вираз в правій частині рівності є ймовірністю того, що випадкова величина   набуває значень менших або рівних  .