Означення

Дисперсією випадкової величини називається математичне сподівання квадрата відхилення цієї величини від її математичного сподівання (середнього значення). Дисперсія є центральним моментом другого порядку. ^[1]

Нехай випадкова змінна може набувати значення відповідно з ймовірностями причому .

• Дисперсія дискретної випадкової величини має такий вигляд:

,

де

і називається стандартним відхиленням величини від її середнього значення ;

— це оператор дисперсії випадкової величини.

• Якщо випадкова величина 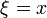задана густиною імовірності, тоді дисперсія виглядає так:^[2]

,

де

, тобто це середнє значення величини ;

— функція густини імовірності.

Твердження

• Якщо є дискретна випадкова величина , сума ймовірностей значень якої менше одиниці, тобто , то дисперсія такої величини визначається так:^[3]

.

Теореми

• Дисперсія являє собою різницю математичного очікування 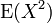квадрата випадкової величини і квадрата середнього значення цієї величини:^[2]

.

• Теорема Чебишова: Ймовірність будь-якої випадкової величини , яка приймає значення в границях стандартних відхилень від середнього значення , не менше , тобто ^[4]

.

• Закон додавання дисперсій: Дисперсія 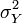суми 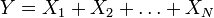дискретних випадкових величин дорівнює алгебраїчній сумі 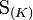значень коваріаційної матриці системи цих величин:^[5]

Властивості

• Дисперсія сталої величини дорівнює нулю, тобто 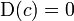, де .

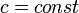• Додавання константи до значень випадкової величини не змінює дисперсії: .

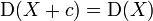• Константу можна виносити в квадраті за знак дисперсії: .

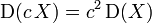• Дисперсія випадкової змінної є невід'ємною величиною, тобто .

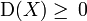Середнє квадратичне відхилення є важливою кількісною характеристикою в статистиці, теорії ймовірностей та оцінки точності вимірювань. Згідно з визначенням середнім квадратичним відхиленням називається корінь квадратний з дисперсії. Однак з цього визначення не зовсім зрозуміло - що характеризує ця величина і як порахувати значення дисперсії.

1. Нехай є кілька чисел, що характеризують будь-які однорідні величини. Наприклад, результати ізмерееній, зважувань, статистичних спостережень і т.п. Всі представлені величини повинні вимірюватися однієї і тієї ж одиницею виміру. Щоб знайти середнє квадратичне відхилення, виконайте такі дії. Визначте середнє арифметичне всіх чисел: складіть всі числа і розділіть суму на загальну кількість чисел.

2. Знайдіть відхилення кожного числа від його середнього значення: відніміть від кожного числа середнє арифметичне значення, порахували в попередньому пункті.

3. Визначте дисперсію (розкид) чисел: складіть квадрати знайдених відхилень і розділіть отриману суму на кількість чисел.

4. Витягніть з дисперсії квадратний корінь. Отримане число і буде середнім квадратичним відхиленням даної множини чисел.

5. Приклад. У палаті лежать сім хворих з температурою 34, 35, 36, 37, 38, 39 і 40 градусів Цельсія. Потрібно визначити середнє квадратичне відхилення від середньої температури. Рішення: • «середня температура по палаті»: (34 +35 +36 +37 +38 +39 +40) / 7 = 37 ° С; • відхилення температур від середнього (в даному випадку нормального значення): 34-37, 35-37, 36-37, 37-37, 38-37, 39-37, 40-37, виходить: -3, -2, - 1, 0, 1, 2, 3 (° С); • дисперсія: ((-3 )?+(- 2 )?+(- 1)? +0? +1? +2? +3?) / 7 = (9 +4 +1 +0 +1 +4 + 9) / 7 = 4 (? С?); • середнє квадратичне відхилення:? 4 = 2 (° С); Відповідь: В середньому по палаті температура - нормальна: 37? С, але середнє квадратичне відхилення температури дорівнює 2? С, що вказує на серйозні проблеми у пацієнтів.

6. Якщо є можливість скористатися програмою Excel, то обчислення дисперсії, а відповідно і середнього квадратичного відхилення можна істотно спростити. Для цього додайте дані вимірювань в один ряд (одну колонку) та скористайтесь статистичної функцією ДІСПР. В якості аргументів функції вкажіть діапазон комірок таблиці, де розміщені введені числа.