Класична модель лінійної регресії

Згідно з класичною моделлю додатково вводяться такі вимоги щодо специфікації моделі і відомих експериментальних даних:

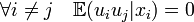• (відсутність кореляції залишків)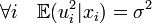

• (гомоскедастичність)

попередні дві властивості можна також записати в матричних позначеннях де I_n — одинична матриця розмірності n.

• Ранг матриці X рівний K+1.

• Усі елементи матриці X є невипадковими.

Часто додається також умова нормальності випадкових відхилень, яка дозволяє провести значно ширший аналіз оцінок параметрів та їх значимості, хоча і не є обов'язковою для можливості використання наприклад методу найменших квадратів:

• 

Для асимптотичних властивостей оцінок додатково вимагається виконання деяких додаткових умов на матрицю X коли її розмірність прямує до безмежності. Однією з таких умов може бути існування границі при прямуванні розмірності до безмежності:

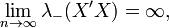• де 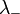позначає найменше власне значення матриці.

Узагальнена модель лінійної регресії

Умови гомоскедастичності та відсутності кореляції між випадковими залишками у моделі часто не виконуються на практиці. Якщо замість цих двох умов у визначенні моделі взяти загальнішу умову:

де — відома додатноозначена матриця, то одержана модель називається узагальненою моделлю лінійної регресії.

Оскільки для кожної додатноозначеної матриці існує матриця така що то модель:

вже буде класичною моделлю лінійної регресії.

34-35-36 Розкрити суть математичної статистики.

Математична статистика — розділ математики, в якому на основі дослідних даних вивчаються імовірнісні закономірності масових явищ. Основними задачами математичної статистики є статистична перевірка гіпотез, оцінка розподілу статистичних імовірностей та його параметрів, вивчення статистичної залежності, визначення основних числових характеристик випадкових вибірок, якими є: вибіркове середнє, вибіркові дисперсії, стандартне відхилення. Прикладом перевірки таких гіпотез є з'ясування питання про те, змінюється чи не змінюється виробничий процес з часом. Прикладом оцінки параметрів є оцінка середнього значення статистичної змінної за дослідними даними. Для вивчення статистичної залежності використовують методи теорії кореляції. Загальні методи математичної статистики є основою теорії похибок.

Математична статистика широко використовує методи теорії ймовірностей. Методи математичної статистики широко застосовують в організації виробництва, радіотехніці, військовій справі, теорії автоматичного керування, біології, економіці, статистичній фізиці, зоряній астрономії тощо. Математичну статистику використовують також при розв'язанні теоретичних і практичних задач кібернетики. Порівняно новим напрямом розвитку математичної статистики є послідовний аналіз та загальна теорія статистичних рішень, яка тісно пов'язана з теорією ігор.

37-38 Розкрити суть статистичної гіпотези.

Гіпотеза — наукове припущення, що висувається для пояснення будь-якого явища і потребує перевірки на досліді та теоретичного обґрунтування, для того щоб стати достовірною науковою теорією. Також - недоведене твердження або здогад. Будь-яка гіпотеза повинна бути спростовуваною хоча б у принципі. Незаперечні припущення (наприклад, аксіоми) гіпотезами не є.

Особливістю гіпотези, як форми наукового знання є те, що вона завжди має певний ступінь імовірності, відмінний від 100%.

Статистичною гіпотезою називається будь-яке припущення щодо виду або параметрів невідомого закону розподілу. У конкретній ситуації статистичну гіпотезу формулюють як припущення на певному рівні статистичної значущості про властивості генеральної сукупності за оцінками вибірки.