9. Случайные величины: дискретные и непрерывные. Закон распределения.

Случайной называют величину, которая в результате испытания принимает одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Cлучайные величины разделяют на дискретные и непрерывные. Дискретной называется случайная величина, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Непрерывной называется случайная величина, которая может принимать все возможные значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно. Законом распределения дискретной случайной величины называют соответствие между ее возможными значениями и их вероятностями.

10. Функция распределения вероятностей и ее свойства.

Ф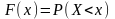 ункцией распределения вероятностей называется функция F(x), определяющая вероятность того, что в результате испытания случайная величина Х примет значение, меньшее х, где х – действительное число:

С войства функции распределения вероятностей.

1. Значения функции F(x) принадлежат отрезку [0,1]:

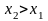
2. Функция F(x) является неубывающей функцией, т.е.

Если

3. Функция F(x) является непрерывной слева.

4 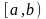. Вероятность того, что случайная величина Х примет значение, заключенное в полуоткрытом интервал равна приращению функции распределения на этом интервале:

5 . Справедливы следующие предельные соотношения:

6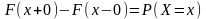 . Функция распределения любой дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений.

7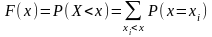 . Зная закон распределения дискретной случайной величины, можно построить функцию распределения:

11. Плотность распределения вероятностей и ее свойства.

Ф ункцией плотности распределения вероятностей (плотностью) непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения

С войства функции плотности.

1. Плотность распределения есть неотрицательная функция:

2. Несобственный интеграл от функции плотности равен единице:

В частности, если все возможные значения случайной

в еличины Х принадлежат интервалу , то

3 . Вероятность попадания непрерывной случайной величины в интервал равна определенному интегралу от плотности распределения, взятому в пределах от a до b :

4.Зная плотность распределения, можно найти функцию распределения:

12. Числовые характеристики дискретных и непрерывных случайных величин, их свойства

Математическим ожиданием дискретной случайной величины Х называется сумма всех ее возможных значений ,умноженных на соответствующие вероятности, т.е.

Д исперсией (рассеянием) дискретной случайной величины Х называется математическое ожидание квадрата отклонения этой величины от ее среднего значения.

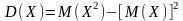
Или

С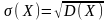 редним квадратическим отклонением случайной величины Х называется корень квадратный из ее дисперсии

Н ачальным моментом порядка дискретной случайной величины Х называется математическое ожидание величины

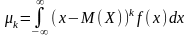
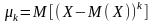
Ц ентральным моментом порядка дискретной случайной величины Х называется математическое ожидание величины :

Центральный момент третьего порядка характеризует степень несимметричности распределения случайной величины относительно ее среднего значения. Величина называется коэффициентом асимметрии.

мода, медиана, эксцесс