МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

БРЯНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Информатика и программное обеспечение»

ПОСТРОЕНИЕ 2-3-ДЕРЕВА, ПОИСК МИНИМАЛЬНОГО И МАКСИМАЛЬНОГО ЭЛЕМЕНТА

Расчетно-графическая работа № 2

по дисциплине «Структуры и алгоритмы обработки данных»

Выполнил: студ. гр. 11-ИиВТ2(с)

________________ Пасецкий И.А.

«___»___________ 2012 г.

Руководитель: доц. каф. ИиПО

________________ Трубаков А.О.

«___»___________ 2012 г.

Брянск 2012

СОДЕРЖАНИЕ

ВВЕДЕНИЕ 3

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 4

Поиск элемента  в 2 – 3 дереве 4

Алгоритм вставки элемента в 2-3 - дерево 6

Удаление элемента из 2 – 3 дерева 8

Алгоритм удаления элемента из 2-3 - дерева 8

2. ПРАКТИЧЕСКАЯ ЧАСТЬ 12

ЗАКЛЮЧЕНИЕ 14

ЛИТЕРАТУРА 15

Введение

Объем хранимой и обрабатываемой информации с каждым годом неуклонно растет и все существенней становится важным вопрос о выборе той или иной структуры данных.

Одна из самых эффективных структур данных является 2-3-дерево, которое и будет рассмотрено в данной расчетно-графической работе.

1. Теоретическая часть

2-3-дерево является идеально сбалансированным деревом поиска. Все пути от корня до любого листа имеют одинаковую длину.

Свойства структуры 2-3 дерева:

	Узлы дерева делятся на два вида - внутренние и листья.
	Элементы множества располагаются только в листьях дерева в линейном возрастающем порядке.
	Внутренний узел имеет 2 или 3 сына  (son1, son2, son3).
	В каждый внутренний узел записывается ключ наименьшего элемента (low2), являющегося потомком второго сына и ключ наименьшего элемента – потомка третьего сына (low3), если третий сын есть.

2-3 - дерево соответствует полному, идеально сбалансированному BST-дереву, если все его узлы являются 2-узлами. В этом случае его высота равна log₂ n. С другой стороны, если все узлы в 2-3 - дереве – 3-узлы, то высота 2-3-дерева равна log₃ n. Таким образом, длина прохода от корня дерева к листьям с элементами и, следовательно, трудоёмкость операций лежит в пределах O(log₃ n) - O(log₂ n).

Поиск элемента в 2 – 3 дереве

Элемент можно найти за время O(log₂ n), сравнивая ключ искомого элемента с параметрами в узлах. Если ключ меньше, чем минимальный элемент у второго сына, то выбирается первый сын. Иначе, если узел имеет двух сыновей, выбирается второй сын. Если есть третий сын, то выбирается второй сын, если ключ меньше минимального ключа третьего сына, или третий сын в противном случае. Таким образом,  поиск приводит к листу с искомым ключом.

 

Включение элемента в 2 – 3 дерево

Включение нового элемента начинается также как и процесс поиска. Пусть мы находимся в некотором внутреннем узле х, чьи сыновья не содержат элемента с заданным ключом k. Если узел содержит двух сыновей, то новый элемент подключается к этому узлу в качестве третьего сына. Новый элемент помещается так, чтобы не нарушить упорядоченность сыновей. После этого корректируются значения минимальных ключей в узле.

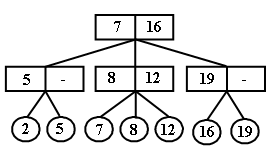
Например, включаем элемент с ключом 18. При поиске мы приходим к самому правому внутреннему узлу x. Помещаем 18 среди сыновей этого узла в порядке 16, 18, 19. В узле x записываются копии ключей 18 и 19.

Если при подключении к узлу, новый элемент является четвертым, то узел х расщепляется  на 2 узла x и x`. Два наименьших элемента переносятся в узел х, а два наибольших – в x`. Теперь надо вставить узел x` среди сыновей родителя х. Здесь ситуация повторяется. Если родитель имеет двух сыновей, то узел x` становится третьим сыном. Если родитель имеет трех сыновей, то он в свою очередь расщепляется на два узла. Процесс восходящего расщепления  идет в случае необходимости выше и может достигнуть корня дерева. При необходимости расщепления корня создается новый корень, сыновьями которого становятся два узла, получившиеся при разбиении старого корня.

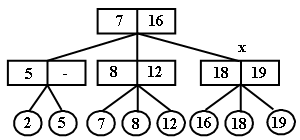
Пусть мы вставляем элемент с ключом 10. Выбранный внутренний узел до подключения имеет трех сыновей, поэтому он разбивается на два  узла.

В свою очередь корень теперь имеет 4  сына и также  разбивается на два узла. При этом создается новый корень, объединяющий два узла, получившихся после разбиения старого корня.