1.6. Фазоманипулированные импульсы
Другим (кроме частотной модуляции) путем расширения спектра является фазовая манипуляция (ФМ). Она заключается в том, что весь радиоимпульс разбивается на ряд парциальных радиоимпульсов, имеющих определенные фазовые сдвиги 2/к. При к>2 манипуляция многофазная, а при к = 2 - противофазная, так как возможны лишь фазовые сдвиги 0 и . Такой случай при длительности парциальных импульсов 0 = и/N иллюстрируется на рис. 1.14, а. При этом сигнал можно представить в виде
uс = Uc соs [0t + (dn - 1)/2],
где dn = ±1 - символ, соответствующий моменту времени 0n, в который осуществляется манипуляция фазы на . Оптимальная обработка такого
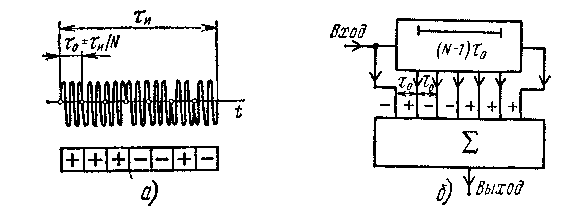
Рис. 1.14. Фазоманипулированный импульс (а) и соответствующий СФ (б)
импульса может производиться с помощью СФ в виде ЛЗ с отводами, причем весовые коэффициенты ±1 расположены зеркально относительно знаков фаз
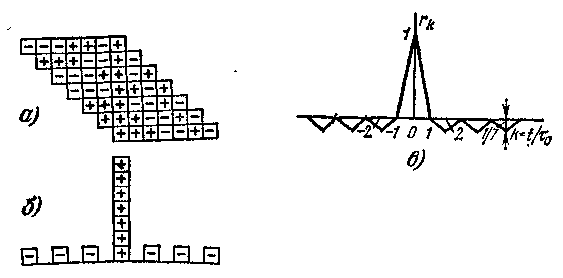
Рис.1.15. Оптимальная обработка ФМ импульса
сигналов (рис. 1.14, б). Заметим, что зондирующий сигнал рис. 1.14, а можно
образовать с помощью той же ЛЗ, если подать короткий радиоимпульс длительностью u/N с обратной стороны линии.
1.6.1. Понятие о фазовой псевдослучайной манипуляции.
В настоящее время уделяется внимание отысканию кодов таких последовательностей, которые обеспечивают максимальный главный лепесток и минимальные боковые лепестки. Для N 13 широко известны коды Баркера.
Ряд исследований показал, что кодов Баркера с боковыми лепестками 1/N при N > 13 не существует. Поэтому использование этих кодов для фазовой манипуляции радиолокационных сигналов обладает ограниченными возможностями с точки зрения коэффициента сжатия. Предложено множество различных кодовых последовательностей, дающих достаточно низкий уровень боковых лепестков автокорреляционной функции выходного сигнала СФ.
Остановимся кратко на так называемых M-последовательностях (последовательности максимальной длительности). Они представляют собой набор символов di (+1 или -1), повторяющихся с периодом N и определяемых произведением двух (или в общем случае большего четного числа) символов в виде
di = -di-n di-k,
где n > k 1, i = (n + 1), .... N.
Число комбинаций n символов из двух элементов +1 и -1 равно 2, из которых 2n-1 положительных и 2n-1 отрицательных. Так как нужно исключить комбинацию из одних отрицательных символов, как не обеспечивающую манипуляцию фазы, то максимальная длина последовательности равна N = 2n-1, причем число отрицательных символов равно 2n-1- 1. (так как в этих последовательностях отличается только порядок следования одинаковых символов, то их можно назвать «зеркальными»).
Число элементов последовательности с ростом N практически удваивается при увеличении n на 1 (N = 1023 при n = 10 и N = 2047 при n = 11 и т. д.). Почти каждому значению n соответствуют несколько чисел k, при котором действует правило di = -d i-n d i-k, хотя они отсутствуют при n = 8, 12, 13, 16 .
Заметим, что если бесконечную последовательность di с периодом в N элементов сдвинуть вправо или влево на некоторое число элементов и применить правило (di = -d i-n d i-k), то получится та же последовательность, смещенная на некоторое число элементов.
Рассматриваемая М -последовательность обладает свойством «хаотичности» и именуется «псевдослучайной». Поясним этот термин. Пусть последовательность образуется подбрасыванием монеты, причем появлению герба соответствует, например, + 1, а цифры -1. Случайный характер такой последовательности определяется тем, что число выпадений + 1 и -1 одно и то же. А также тем, что половина числа серий последовательных состояний одного и того же вида имеет продолжительность (длину), характеризуемую единицей, четвертая часть - числом 2, восьмая часть - числом 3 и т. д. Кроме того, функция автокорреляции имеет пик в начале отсчета, быстро спадающий при удалении от него.
Сказанное хорошо выполняется в М-последовательностях, так как число +1 за период Т всего на единицу больше числа -1. Выполняется также условие для продолжительности числа последовательных состояний одного и того же вида при условии, что рассматриваемое число серий превышает 1.
Боковые лепестки для периодической М-последовательности спадают по сравнению с главными в 1/N раз. Однако для усеченной М-последовательности в один период N боковые лепестки имеют порядок 1/N1/2. Это хуже, чем для кода Баркера, но достаточно для ряда приложений.
Формировать и обрабатывать ФМ сигналы на основе М-последовательностей можно с помощью достаточно простых устройств, использующих линейные переключатели на основе регистров сдвига.
Для подавления боковых лепестков также следует использовать весовые усилители. При этом улучшается отношение сигнал-шум, но в отличие от ЛЧМ сигналов расширяется не главный максимум, а область боковых лепестков выходного сигнала. При синтезе различают два критерия: максимизация отношения максимума главного лепестка к максимуму бокового (-фильтры); максимизация отношения максимума главного лепестка к корню квадратному из суммы квадратов боковых лепестков (-фильтры).