1.5. Сложные радиолокационные сигналы

1.5.1. Противоречие между различными предельно достижимыми параметрами рлс.

Дальность действия РЛС, как и других радиоустройств, в случае оптимальной обработки сигнала и заданной спектральной плотности шума зависит от энергии зондирующего сигнала независимо от его формы. Так, для пачки прямоугольных импульсов с прямоугольной огибающей полная энергия Еc= NР_и_и, т. е. дальность при заданной скорости обзора (определяющей число импульсов N) зависит от энергии импульса. Учитывая, что предельные мощности электронных приборов и антенно-фидерных трактов (например, волноводов) ограничены, увеличение дальности неизбежно связано с повышением длительности импульсов, т. е. со снижением потенциальной разрешающей способности по дальности (D_ПОТ = сu/2). Поэтому требования большой дальности и высокой разрешающей способности противоречивы.

Потенциальная точность измерения всех координат цели также определяется энергией импульса, так как зависит от отношения 2Е₀/N₀. Вместе с тем рост энергии за счет увеличения длительности импульса уменьшает ширину спектра и неизбежно ухудшает потенциальную точность измерения дальности. Что касается измерения скорости, то при увеличении длительности импульса повышается потенциальная точность и уменьшается диапазон неоднозначного измерения скорости.

Таким образом, увеличение длительности обычного (гладкого) импульса позволяет увеличить дальность действия, точность и однозначность измерения скорости (а также точность измерения угловых координат), но снижает разрешающую способность и точность измерения дальности. Радикальный способ разрешения указанного противоречия - переход к сложным сигналам.

Сложными называются такие сигналы, база которых, т. е. произведение ширины спектра fс на длительность Т₀, удовлетворяет условию fcТ₀ > 1. Заметим, что определение ширины спектра и длительности сигнала является условным. Если сигнал занимает конечное время, то его спектр простирается в бесконечном интервале частот. Аналогично если спектр занимает конечный интервал, то соответствующий сигнал существует по оси времени в интервале от - до +. Однако при обычных сигналах и принятых уровнях отсчета длительности и ширины спектра их произведение имеет порядок единицы. Например, для прямоугольного импульса длительностью u„ ширина спектра часто определяется первым нулем, т. е. равна 1/u, так что fcТ₀ = 1. Естественно, что при других уровнях отсчета можно получить большие значения произведения. Однако в сложных сигналах речь идет о том, что произведение значительно возрастет при тех же уровнях отсчета. Это обеспечивается за счет внутриимпульсной частотной или фазовой модуляции. Сложные сигналы не исчерпываются одиночными импульсами. Например, когерентная пачка импульсов может рассматриваться как один сложный сигнал

1.5.2. Частотно-модулированные импульсы

Выше уже говорилось, что для обеспечения большой дальности РЛС требуются импульсы большой длительности. Для получения же высокой разрешающей способности по дальности выходной сигнал СФ, т. е. автокорреляционная функция сигнала, должен иметь малую длительность. Это соответствует большей ширине спектра на выходе СФ. Учитывая, что амплитудно-частотные характеристики СФ и спектра сигнала совпадают, ширина спектра сигнала на входе СФ должна быть ненамного шире, чем на его выходе, т. е. практически того же порядка. Обеспечение такой ширины спектра без снижения дальности РЛС возможно, если в импульсах достаточно большой длительности производить частотную (или фазовую) модуляцию несущей частоты.

Рассмотрим СФ для импульсов с линейной частотной модуляцией (ЛЧМ), в котором для упрощения выкладок форма огибающей принята колоколообразной.

Таким образом, амплитудно-частотный спектр колоколообразного импульса с ЛЧМ имеет также колоколообразную форму со средним значением, равным несущей частоте ₀, а ширина этого спектра тем больше, чем больше скорость изменения частоты .

Согласованный фильтр (СФ) для рассматриваемого импульса имеет частотную характеристику, комплексно-сопряженную со спектром полезного сигнала. В данном случае при оптимальной фильтрации импульсов с ЛЧМ особое значение имеет согласование фазовых характеристик. Поэтому для простоты можно принять амплитудно-частотную характеристику СФ равномерной, а его фазочастотную характеристику согласованной с фазовым спектром сигнала.

Ширина спектра импульса с ЛЧМ мало отличается от величины девиации частоты. При этом его гармонические составляющие имеют различные фазы. После прохождения импульса через фильтр все гармонические составляющие становятся в определенный момент времени синфазными и суммируются арифметически. Так как таких составляющих много (большая ширина спектра), то синфазное суммирование приводит к увеличению пикового значения, а в силу закона сохранения энергии - к такому же уменьшению длительности, т. е. сужению импульса.

Итак, амплитуда импульса возрастает в m^1/2 раз (т. е. мощность в импульсе в m раз), а его длительность уменьшилась в m раз. Коэффициент m назовем коэффициентом сжатия.

Коэффициент сжатия может быть представлен в простой форме. Если девиацией частоты fм назвать ее изменение в течение длительности _0.5, то _0,5 = fм. Интерес представляет случай достаточно больших m, так что

mfм _0.5

коэффициент сжатия равен произведению девиации частоты на длительность, т. е. базе сигнала, что является достаточно общим правилом (например, для импульсов с прямоугольной огибающей и др.).

В процессе объяснения не учитывалось действие АЧХ. Так как она повторяет форму амплитудно-частотного спектра сигнала, то происходит лишь некоторое сужение спектра сигнала. Легко показать, что оно равно . Соответственно длительность сжатого импульса увеличится в раз, т. е. коэффициент сжатия уменьшится практически незначительно.

Следовательно, при оптимальной обработке импульса с ЛЧМ получается эффект сжатия: при наличии достаточной энергии зондирующего импульса, имеющего большую длительность, сохраняется высокая разрешающая способность по дальности. Заметим, так как дальность при оптимальной обработке зависит от энергии импульса, то сжатие не дает никакого выигрыша в дальности.

Анализ спектра такого импульса длительностью и и девиацией fм показывает, что по мере увеличения произведения fм_и спектр импульса делается все более равномерным.

Однако сжатый импульс имеет боковые лепестки, которые нежелательны, так как ухудшают разрешающую способность и создают дополнительные помехи. Для уменьшения боковых лепестков надо вместо идеального фильтра использовать фильтр с резко спадающей, но плавной (например, колоколообразной) АЧХ. Для уменьшения боковых лепестков уже после сжатия можно применить весовую обработку - пропускание сжатого импульса через фильтр со специально подобранной характеристикой. Уменьшение боковых лепестков сопровождается некоторым расширением главного лепестка. Описанная задача полностью аналогична задаче ослабления боковых лепестков в антенне.

Анализ обработки сигналов с дискретным изменением частоты поучителен с точки зрения понимания процессов при обработке ЛЧМ импульсов. Рассмотрим импульс общей длительностью N, включающий N следующих один за другим прямоугольных парциальных импульсов длительностью , частота которых сдвигается от импульса к импульсу скачком на величину f от f₀ до f₀ + (N - 1) f.

Устройство оптимальной обработки содержит линию задержки (ЛЗ) с общим временем задержки (N - 1) с отводами, соответствующими длительности , в цепи которых включены полосовые фильтры, настроенные на частоты парциальных импульсов (рис. 1.10). Для реализации СФ требуется, чтобы полосовые фильтры были согласованными для парциальных импульсов. Кроме того, на рис. 1.10 показаны усилители, с помощью которых можно влиять на форму огибающей выходного (сжатого) импульса.

Полосовые фильтры пропускают все парциальные импульсы одновременно лишь в интервале (N- 1)  t  N, когда первый из них достигнет конца ЛЗ.

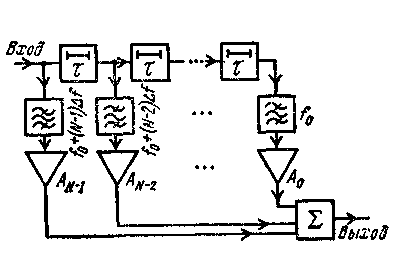
Рис. 1.10. Оптимальная фильтрация сигнала

На рис. 1.11 показан механизм формирования огибающей при N = 8 на неограниченном интервале времени. Для получения эффекта сжатия требуется синфазность векторов, характеризующих отдельные частотные составляющие. Это выполняется в точках k/f, где k - целое число. На рис. 1.11 также показано расположение векторов в нулевых точках и для боковых максимумов. Как видно, ширина главных максимумов (по нулям) равна 2/Nf, а на уровне 4 дБ от максимума длительность равна 1/Nf , причем максимумы следуют с периодом 1/f.

Для рассматриваемого случая сложения парциальных импульсов, если = 1/f, в пределах участка сжатия на выходе устройства обработки будет находиться лишь один главный лепесток длительностью сж  1/Nf  /N, т. е. коэффициент сжатия, как и следовало ожидать, равен базе сигнала:

m = N/сж  NNf /  N².

При наличии многих целей, когда требуется работа в широком динамическом диапазоне принимаемых сигналов, боковые лепестки будут создавать мешающие сигналы. Поэтому важной задачей устройств обработки является подавление боковых лепестков. Для подавления боковых лепестков выходного сигнала в схеме рис. 1.10 требуется «весовая обработка» парциальных импульсов путем подбора весовых коэффициентов Ак.

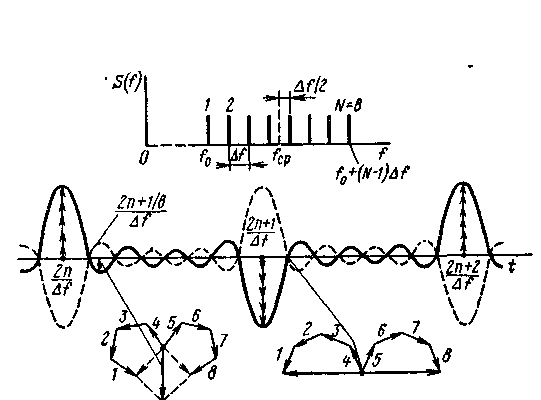
Рис.1.11. Эффект сжатия при дискретном изменении частоты гармонических составляющих

Частотно взвешенная функция, образованную с помощью усилителей с коэффициентами усиления Ак (рис. 1.10), каждый из которых соответствует определенной частотной составляющей сигнала, выделяемой полосовым фильтром. Благодаря линейной зависимости частоты от времени  = ₀ + t в пределах длительности импульса частотной функции К () соответствует эквивалентная ей временная функция, образованная с помощью тех же коэффициентов Ак. На этом основано понятие временного взвешивания.

Таким образом, можно использовать либо временное взвешивание излучаемого сигнала, либо частотное при обработке сигнала в приемнике. При временном взвешивании средняя энергия передаваемого сигнала выбирается равной энергии сигнала с прямоугольной огибающей, то отношение сигнал-шум на выходе приемника не зависит от того, где производится весовая обработка. Если же, как это чаще бывает, ограничена пиковая мощность, то предпочтительнее всю весовую обработку производить в приемнике.

В заключение отметим связь весовой обработки сигналов с формированием ДН антенны. Дело в том, что задачи выбора распределения поля в раскрыве антенны и фильтра весовой обработки К () равнозначны. Например, известно распределение поля, при котором формируется наиболее узкий луч для заданного уровня боковых лепестков в случае решетки больших размеров с равномерно расположенными синфазными точечными источниками (распределение Дольф-Чебышева).

Выше было показано, что использование СФ для импульсов с ЛЧМ (рис.1.12) обеспечивает эффект их сжатия. Если импульсы обладают большой базой (fми » 1), то амплитудно-частотный спектр близок к прямоугольному, а фазочастотный - к квадратичному. Согласованный фильтр должен иметь полосу пропускания, равную девиации частоты fм, и обладать дисперсионной характеристикой в виде линейной зависимости времени группового запаздывания от частоты, наклон которой является обратным по отношению к изменению частоты внутри импульса. Заметим, что дисперсия фильтра определяется квадратичностью его фазовой характеристики  (), при которой время группового запаздывания tгр = d ()/d

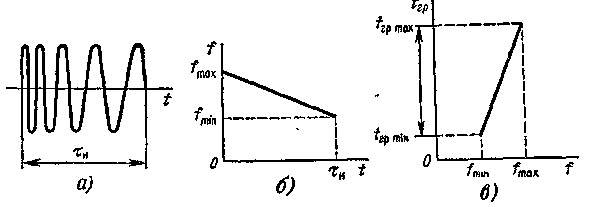
Рис. 1.12. Прямоугольный импульс с ЛЧМ и условие его оптимальной обработки

является линейной функцией частоты (в отличие от обычных фильтров, где tгр const). На рис. 1.12, а, б показаны импульс с ЛЧМ и характер изменения частоты в пределах длительности этого импульса. Если такой импульс проходит через фильтр, у которого зависимость времени группового запаздывания от частоты tгр (f) имеет вид, показанный на рис. 1.12, в, то это обеспечивает эффект сжатия. Действительно, фильтр ускоряют низкочастотные составляющие у среза импульса (tгр меньше) и замедляет составляющие с более высокими частотами у фронта импульса (tгр больше). При выборе значений tгр _min и tгр _max (соответствующих частотам fгр _min и fгр _max импульса) следует исходить из условия tгр _max - tгр _min = _и, так как слишком малая разность задержек дает неполное сжатие, а слишком большая - расширение сжатого импульса. Степень сжатия определяется, как было показано выше, величиной девиации частоты fм. Длительность сжатого импульса равна примерно 1/fм.

Дисперсионная ультразвуковая линия задержки (ДУЛЗ) представляет собой ультразвуковой волновод в виде плоской тонкой алюминиевой или стальной пластины с пьезопреобразователями на концах. Дисперсией обладает первый продольный тип колебаний.

Недостатком ДУЛЗ является то, что при широкой полосе f _л толщина пластины оказывается очень малой. Для расширения полосы используется скачкообразное или плавное изменение толщины по длине. Это эквивалентно последовательному соединению нескольких ДУЛЗ.

Получают развитие пьезоэлектрические многоотводные ЛЗ, использующие поверхностные акустические волны (ПАВ), у которых в качестве звукопровода применяются пьезоэлектрические материалы (естественный или синтетический пьезокварц, ниобат лития и др.). Возбуждение и съем электроакустических колебаний осуществляются с помощью металлических решетчатых электродов. На рис. 1.13, а показан вариант ЛЗ с неэквидистантным расположением электродов. Импульсная характеристика такой ЛЗ (реакция на короткий видеоимпульс) –

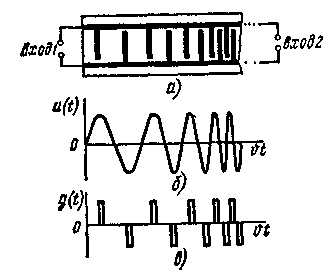
Рис. 1.13. Пьезоэлектрические многоотводные ЛЗ, использующие ПАВ

последовательность видеоимпульсов одинаковой длительности с переменным периодом повторения (рис. 1.13, в). С помощью полосовых фильтров при этом можно выделить ЛЧМ сигнал (рис. 1.13, б), который используется как зондирующий.

Такой импульс после отражения от цели поступает с выхода приемника на вход 2 (рис. 1.13, б) для обработки в СФ, т. е. для сжатия. Этот импульс является зеркальным отображением импульсной характеристики фильтра сжатия. В рассматриваемой ЛЗ на ПАВ число электродов может быть доведено до коэффициента сжатия. Интегральное исполнение с применением фотолитографической планарной технологии позволяет получить число электродов каждой гребенки примерно 10⁴.

Для сжатия импульсов малой длительности с большой девиацией частоты (десятки или сотни мегагерц) может применяться ЛЗ с отводами и полосовыми фильтрами со смещенными характеристиками в цепи каждого отвода.

При движении цели, когда частота отраженного сигнала сдвигается на Fд, происходит сдвиг частот fmах и fmin. Соответственно сдвигаются значения tгр. В зависимости от знака доплеровского смещения сжатый импульс появляется на выходе раньше (-Fд) или позже (+Fд), чем импульс неподвижной цели. При этом можно разделить сдвиги, определяемые дальностью и скоростью, если чередовать направления включения генераторного и сжимающего фильтров.

В заключение отметим, что в принципе достигнуты коэффициенты сжатия порядка нескольких тысяч и даже 10⁶, хотя пока на практике используются значительно меньшие коэффициенты сжатия.