5.3.2. Квазиоптимальные фильтры для одиночных импульсов.

Как правило, при реализации СФ для одиночных импульсов простой формы (имеются в виду импульсы с немодулированной по фазе или частоте несущей) используются так называемые квазиоптимальные фильтры, реализуемые с помощью обычных усилителей (например, в тракте ПЧ), имеющих оптимальную полосу пропускания.

При переходе от видеочастотного усилителя к резонансному радиочастотному оптимальная полоса возрастает вдвое (вместо 0,2/_и становится 0,4/_и), а проигрыш относительно СФ остается тем же. В общем случае оптимальная полоса пропускания приемника (радиочастотного усилителя) на уровне 0,707

f_проп=/_u,

где , изменяется от 0,4 до 0,67 для радиоимпульса с прямоугольной огибающей при увеличении числа каскадов резонансного усилителя с n = 1 до n = 5 и = 1,37 для идеализированной прямоугольной частотной характеристики.

5.3.3. Сф для пачки импульсов.

Как уже отмечалось, спектр последовательности некогерентных импульсов не отличается от спектра одиночных радиоимпульсов. В этом случае вместо СФ целесообразно использовать квазиоптимальный в виде полосового усилителя (например, УПЧ), полоса которого согласована с длительностью импульса. Что касается пачки когерентных импульсов, то здесь при построении СФ сохраняется связь между частотными характеристиками радио- и видеоимпульсов.

Рассмотрим ограниченную пачку видеоимпульсов, состоящую из N импульсов, следующих через интервал времени Т_ц (рис. 5.9, а), которую можно представить в виде суммы.

,

где функция u_u(t) характеризует отдельные импульсы пачки, а U_k = U(kT_n) - их огибающую.

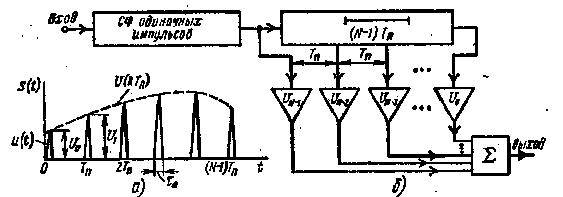
Рис. 5.9. Согласованный фильтр для пачки импульсов

Оптимальный фильтр для пачки импульсов представляет собой последовательное (каскадное) включение СФ для одиночного импульса пачки и накопителя с весовым суммированием. Последний можно представить в виде ЛЗ с отводами, время задержки между которыми равно Т_п (рис. 5.9, б). Таким образом, оптимальная обработка пачки импульсов с помощью СФ осуществляется в два этапа: внутрипериодная обработка, происходящая в СФ для одиночных импульсов пачки, и межпериодная обработка в накопителе.

Накопитель, описываемый частотной характеристикой К_z (), у которого весовые коэффициенты равны амплитудам импульсов пачки, расположенным в обратном порядке, обеспечивает в момент окончания пачки Т₀  (N - 1)Т_п суммирование всех импульсов пачки со «своими собственными» весовыми коэффициентами, т. е. амплитуда N-го импульса сигнала плюс шум на выходе накопителя

,

где Х₁ - амплитуда импульсов сигнала плюс шум на входе.

Таким образом, импульс малой амплитуды вместе с шумом умножается на малый весовой коэффициент, а импульс большой амплитуды вместе с шумом - на большой весовой коэффициент. Такое рациональное «взвешивание» и позволяет обеспечить максимум отношения пикового значения сигнала к шуму. При этом в общем случае имеет место неравновесное суммирование, а в случае пачки с прямоугольной огибающей - простое равновесное суммирование. Такой накопитель именуется накопителем группового действия. Найдем теперь форму пачки импульсов на выходе СФ. Пусть пачка имеет прямоугольную огибающую и состоит из прямоугольных импульсов (рис. 5.10, а). На выходе СФ для одиночных импульсов образуется пачка треугольных импульсов (рис. 5.10, б). Далее, так как амплитуды всех импульсов равны, происходит равновесное суммирование сдвинутых импульсов (рис. 5.10, в, г), в результате которого амплитуда импульсов пачки линейно растет и затем падает (рис. 5.10, д). Таким образом, изменение огибающей пачки на выходе СФ аналогично изменению формы одиночного импульса. Точно

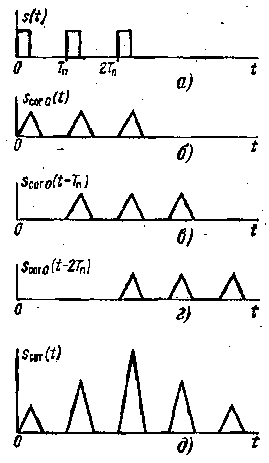
Рис.5.10. Пачка импульсов на выходе СФ

такую же форму имеет огибающая когерентных радиоимпульсов, если использовать СФ для отдельных радиоимпульсов и выполнить условия когерентного сложения.

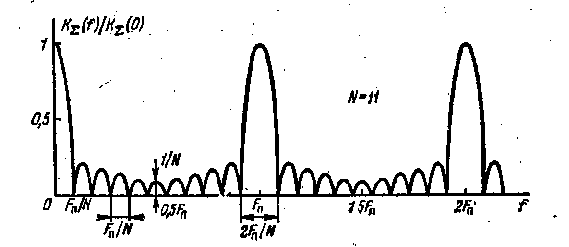
5.11. Амплитудно-частотная характеристика (АЧХ) накопителя группового действия

При симметричной огибающей, имеются главные «зубья» шириной (на нулевом уровне) 2Fn/N (кроме нулевого зуба, имеющего ширину F_n/N) на расстоянии F_n друг от друга и боковые зубья шириной F_n/N. Минимальная их амплитуда в точках F_n/2, 3F_n/2,... (посередине между главными лепестками) равна единице, так что отношение максимальных амплитуд зубьев к минимальным равно N, т. е. минимальная амплитуда зубьев достигает величины 1/N.

Кроме того ширина главных зубьев на уровне 0,707 приблизительно равна

F_0,7=F_n/N=1/(NT_n).

При увеличении числа импульсов N ширина зубьев уменьшается. В пределе при N  (периодическая последовательность импульсов) F_0,70 и боковые лепестки исчезают. Характеристика накопителя остается без изменения в случае пачки радиоимпульсов. Происходит лишь перенос в область несущей частоты характеристики СФ для одиночных радиоимпульсов. Следует, однако, отметить, что техническая реализация радиочастотного накопителя гораздо сложнее, чем видеочастотного. На рис. 5.12 показаны АЧХ, СФ для соответствующих сигналов.

Сказанное выше доказывает, что СФ для пачки импульсов является гребенчатым фильтром (ГФ). Так как полосы прозрачности расположены на частотах, кратных частоте повторения F_п, то такой фильтр можно назвать полосовым гребенчатым фильтром (ПГФ). В принципе при низкой скважности, когда общая ширина полосы СФ, определяемая шириной спектра одиночных импульсов, составляет небольшое число F_n, ПГФ можно реализовать с помощью набора узкополосных фильтров.

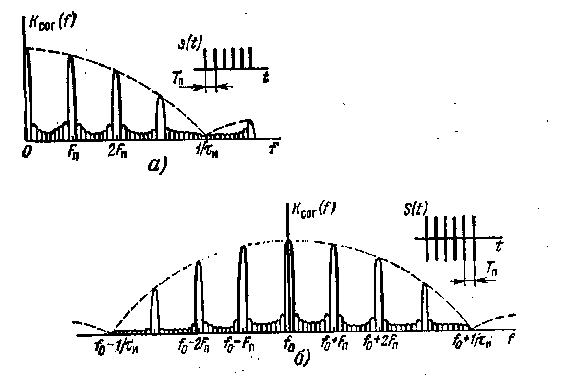
Рис. 5.12. Амплитудно-частотные характеристики СФ для пачек видеоимпульсов и радиоимпульсов

В гребенчатом фильтре особенно наглядно виден механизм оптимальной фильтрации. Дело в том, что полосы прозрачности главных зубьев ГФ пропускают основную часть энергии спектра импульсов. Поэтому максимальная амплитуда импульсов снижается к концу пачки незначительно. Что же касается помехи, обладающей равномерным спектром, то ее мощность определяется результирующей полосой пропускания и поэтому уменьшается значительно. Сравним отношение сигнал-шум на выходах ПГФ и квазиоптимального фильтра для одиночного импульса. Только на основе фильтровых свойств ПГФ, предполагая, что амплитуды импульсов на выходе рассматриваемых фильтров одинаковы. Поэтому выигрыш в отношении сигнал-шум, даваемый ПГФ, обратно пропорционален отношению мощностей помехи на выходах фильтров, которые, в свою очередь, пропорциональны соответствующим полосам. Для прямоугольных импульсов можно ограничить полосу величиной 1/_и. В пределах этой полосы имеются 1/_иF_n зубьев. Эффективная полоса каждого зуба, приблизительно равная полосе на уровне 0,707, близка к F_n/N, т. е. общая (шумовая) полоса равна (1/_uF_n)F_п/N. Поэтому выигрыш в отношении сигнал-шум по мощности равен N.

Соответствующее отношение по напряжению равно .

Можно сделать вывод на основании того, что энергия пачки из N одинаковых импульсов в N раз больше энергии одного импульса.

Описанный выше процесс оптимальной фильтрации легко объясняется на основе механизма накопления, показанного на рис. 5.10 (без шумов). В процессе накопления максимальная амплитуда сигнала возрастает в N раз, а энергия и мощность - в N² раз. Так как шумы состоят из флуктуационных выбросов, появляющихся в случайные моменты времени, то они накапливаются медленнее. Сложение таких некоррелированных выбросов происходит, не арифметически, а геометрически, т. е. энергия и мощность растут пропорционально числу складываемых порций N. Таким образом, отношение сигнал-шум растет в N²/N = N раз.

Таким образом, при синтезе квазиоптимальных фильтров для реальных сигналов следует обращать основное внимание на главные зубья частотной характеристики и уменьшать по возможности уровень боковых зубьев.