3. Влияние движения цели на преобразованный сигнал.

Симметричный пилообразный закон модуляции обеспечивает возможность разделения частот биений, определяемых дальностью, и доплеровского сдвига частоты, возникающего из-за движения цели.

Так как частота передатчика меняется, то доплеровский сдвиг отраженного сигнала также меняется от частоты. Однако можно пренебречь изменением доплеровской частоты за период модуляции и считать

Fd min  , Fd max = Fd.

На рис. 3.37, a, б pассмотрен случай сближения с целью, когда доплеровский сдвиг добавляется к функции fс (t) и она смещается вверх на величину Fд. Cреднее значение частоты биений Fбср = (Fb₁ + Fb₂)/2 = Fb0 пропорционально дальности D, а уклонение от среднего значения

(Fb₁ - Fb₂)/2 = Fd пропорционально радиальной скорости цели vр.

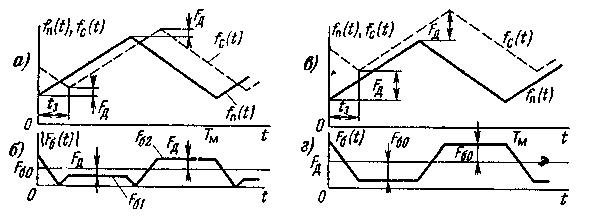
Рис. 3.37. Частота биений при движении цели

Если в приемном устройстве разделить переменную и постоянную составляющие функции Fb (t) то можно раздельно измерить дальность и радиальную скорость цели. Для этого надо произвести соответствующее переключение в каждом полупериоде модуляции.

При большой скорости цели, когда Fд> Fбо, кривая fс (t) лежит выше fи (t) и ее пересекает (рис. 3.37, в). В этом случае частота преобразованного сигнала меняется через каждые пол периода, но зоны обращения со скачком фазы на 180° отсутствуют (рис. 3.37, г).

4. Понятие об измерении дальности методом счета числа импульсов.

РЛС с частотной модуляцией обычно применяются в качестве бортового радиовысотомера. При этом имеется лишь одна цель - земная поверхность, которую в первом приближении для гладкой поверхности можно считать точечной (случай зеркального отражения). Применение спектрального анализа при наличии одной цели не целесообразно. Здесь нашел широкое применение весьма просто реализуемый метод измерения частоты биений путем счета числа импульсов преобразованного сигнала. При этом преобразованный сигнал (рис. 3.38, а) подвергается ограничению и дифференцированию (рис. 3.38, б), после чего положительные или отрицательные импульсы запускают формирователь, вырабатывающий стандартные импульсы (определенной амплитуды, длительности и формы). Последние заряжают накопительный конденсатор счетчика. При

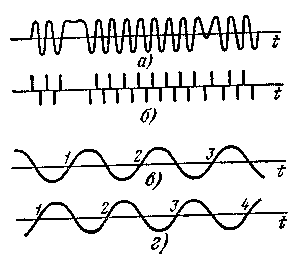
2.38. Метод счета числа импульсов

симметричном пилообразном законе модуляции число импульсов за период модуляции равно

.

Число импульсов в секунду, т. е. средняя частота повторения импульсов, фиксируемая счетчиком, .

Существенным фактором, влияющим на счет числа импульсов, является «паразитная» амплитудная модуляция зондирующего и отраженного сигналов, вызванная резонансными свойствами колебательных систем передатчика, входа приемника и антенн, вибрациями, флуктуациями коэффициента отражения. Влияние паразитной модуляции можно уменьшить применением балансного смесителя.

Следует отметить, что на практике проще реализовать не пилообразный, а синусоидальный (см. рис. 2.32, в) закон модуляции. При этом частота биений все время меняется. Однако можно показать, что среднее значение этой частоты такое же, как а в предыдущем случае

.

Имеется ряд способов устранения влияния дискретности отсчета. В частности, весьма эффективным может оказаться непосредственное измерение длительности периодов колебаний преобразованного сигнала, которые являются монотонной функцией дальности. Следует, однако, отметить, что дискретность проявляется только в статических условиях. При отражении от реальной цели в условиях полета происходит усреднение, устраняющее влияние дискретности.