2.7.6. Зона видимости рлс

Зоной видимости называется часть воздушного пространства, внутри которого обеспечивается обнаружение определенных целей с вероятностью правильного обнаружения не менее требуемой при заданной вероятности ложной тревоги. Как правило, пользуются сечением зоны видимости в различных плоскостях. Наиболее важным для наземных РЛС является сечение в вертикальной плоскости, проходящее через точку установки антенны РЛС и называемое диаграммой видимости. Она характеризует зависимость дальности обнаружения от высоты или угла места цели.

Более удобной для изображения зоны видимости оказывается прямоугольная система координат H, D, в которой могут быть нанесены прямые угла места, полученные из соотношения sin  = Н/D.

Рассмотрим теперь некоторые характерные особенности диаграммы видимости. На рис. 2.27, а изображена диаграмма направленности (ДН) в плоскости угловой координаты а (например,  или ). Геометрическим местом расположения точечных изотропных целей с одинаковыми ЭОП,

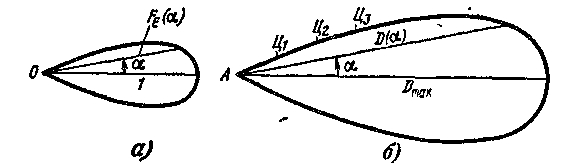
Рис. 2.27. Диаграмма направленности (а) и геометрическое место расположения одинаковых целей (б), при котором отраженные сигналы одинаковы. А -точка расположения РЛС

при котором максимальная дальность обнаружения одинакова, в полярной системе координат является кривая D () = DmFE () (рис. 2.27, б), подобная кривой FE() (рис. 2.27, а). Следовательно, для получения одинаковой максимальной дальности обнаружения целей, расположенных на одной и той же высоте, требуется, согласно сказанному выше, чтобы ДН в полярной системе координат имела в пределах некоторых крайних углов _min, _max: горизонтальный участок (рис. 2.28, а). Тогда одинаковые цели Ц1, Ц2 дадут одинаковые амплитуды отраженных сигналов. В случае же целей с различными отражающими свойствами амплитуды отраженных сигналов будут зависеть от отражающих свойств цели, но не от дальности. Это помогает оценить размеры цели.

Аналогичное явление происходит при облучении земной

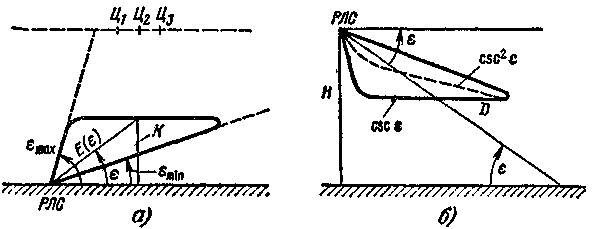
Рис. 2.28. Косекансные ДН

поверхности. Здесь для получения одинаковых амплитуд отраженных сигналов от одинаковых целей на земной поверхности, находящихся на разной дальности, требуется, чтобы нижний участок ДН был горизонтальным (рис. 2.28, б).

Для аналитической записи основного горизонтального участка ДН по напряженности поля Е () в полярной системе координат воспользуемся рис. 2.28, а, откуда следует, что Е() = К сsс . Такая ДН носит название косекансной. В нормированном виде при _min <  < _mах она записывается как

.

Диаграмма направленности по мощности пропорциональна величине Е2 (), т. е. сзс² , а следовательно, (см. пунктир на рис. 2.28, б)

FР () = сsс² ()/ csс² _min.

Как видно, в данном случае точечных изотропных целей требуемая для обеспечения одинаковой дальности (одинаковой мощности сигнала на входе приемника) косекансная ДН FE() отличается от случая отражения от диффузной поверхности множителем (соs )^1/4.

Диаграмма видимости определяется путем расчета, однако, как правило, все факторы, влияющие на максимальную дальность действия и на результирующую ДН, учесть трудно, так что окончательная корректировка зоны видимости производится путем облета РЛС. На рис. 2.29 показаны реальные диаграммы видимости некоторых РЛС УВД и сектор обзора (диаграмма видимости) с угловым размером  и радиусом D₀,

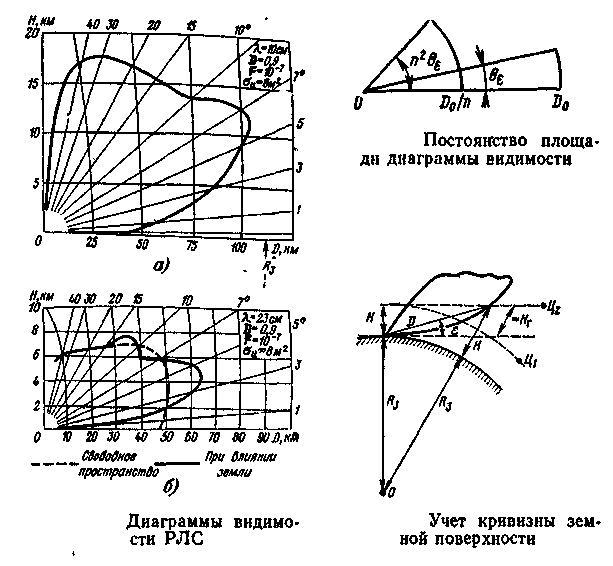
Рис. 2.29. Диаграммы видимости некоторых РЛС УВД

просматриваемый РЛС. Площадь сектора равна D₂₀/2. Пусть теперь максимальная дальность уменьшится в n раз до D₀/n. В этом случае при прочих равных условиях (т. е. при тех же полной излучаемой мощности, способах обзора и обработки) коэффициент усиления антенны согласно уравнению радиолокации (D₀ ~ G^1/2) падает, как G ~ 1/n². Учитывая, что G~ 1/_угол зоны видимости возрастает до n². Таким образом, площадь диаграммы видимости остается той же: D₂₀/2.

Если теперь учесть азимутальный размер зоны видимости D₂₀_. то полный объем, просматриваемый при обзоре, V ~ D₀, т. е. полный объем пропорционален радиусу зоны видимости с постоянной площадью в вертикальной плоскости.

Из постоянства площади диаграммы видимости РЛС следует, что при увеличении потолка зоны до 2H, дальность ее уменьшается до D₀/2, откуда просматриваемый объем V также уменьшается вдвое.

Кривизна земной поверхности ограничивает предельную дальность РЛС дальностью прямой видимости, которая, как известно, равна

Dnp=(2R3)^1/2(H^1/2+hA^1/2)

где Rз = 6370 км - радиус Земли; h_A - высота антенны, а H - высота цели над земной поверхностью.

Так как обычно H »h_А, то D_Пр  (2R3H)^1/2 или Dnр  113 H^1/2 км. С учетом нормальной рефракции следует пользоваться эквивалентным радиусом Земли R3э = 4Rз/3, откуда Dnрэ  130 H^1/2 км. Кроме того, кривизна земной поверхности приводит к уменьшению дальности обнаружения цели Ц1, пролетающей на одной и той же высоте над поверхностью земли, по сравнению с целью Ц2, которая находится на одной и той же высоте над плоскостью горизонта. Это связано с тем, что первая цель пересекает границу показанной на рис. 2.29 диаграммы видимости на более близком расстоянии. Вместе с тем цели, скрытые за горизонтом, в обычных условиях вообще не обнаруживаются.

Связь между высотой цели над горизонтом Рг и истинной высотой Н определяется с помощью поправки Н:

Н = Н - Нг  D2/2R3.

Чтобы учесть кривизну Земли, после построения обычной диаграммы видимости в прямоугольных координатах H, D надо провести в масштабе дуги равных высот H, соответствующие радиусу земли Rзэ (рис. 2.29, а). Другой способ основан на том, что все точки зоны видимости, а также точки линий равных углов места приподнимают на величину высотной поправки H -Hг, так что координатная сетка остается прямой, а линии равных углов места искривляются.

Следует отметить, что кривизна земли вызывает еще сферическую расходимость при отражении и дифракцию. Сферическая расходимость в пределах площади вблизи антенны, участвующей в формировании отраженного луча, мала. При этом большее влияние оказывает не кривизна Земли, а рельеф местности. Поэтому влиянием этого фактора на диаграмму видимости можно в первом приближении пренебречь. То же относится к дифракции на очень высоких частотах радиодиапазона.

В настоящее время для практических расчетов рекомендуется логарифмическая форма обобщенного уравнения дальности РЛС. В связи с этим обобщим простейшее уравнение дальности. Введем вместо квадрата коэффициента усиления G2, используемого в случае одной приемопередающей антенны, произведение коэффициентов усиления приемной и передающей антенны Gп Gпр. Аналогично интерференционный множитель земли Fзем разобьем на множители передающей Fп и приемной, F_Пр антенн так, что Fаем () = (Fn Fnpп)^1/2Таким образом, в числителе уравнения дальности следует заменить G2 на GпGnp,, и Fаем () = (Fn Fnpп)^1/2.

Учитывая сказанное выше, запишем обобщенное уравнение дальности в свободном пространстве

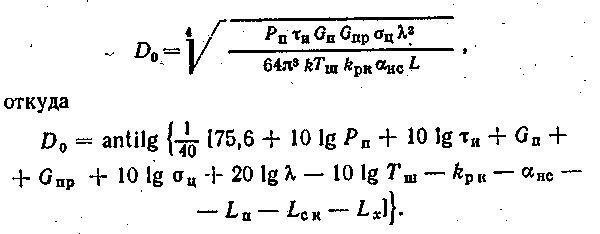
В этой формуле D₀ выражается в километрах, Рn в ваттах, Gn, G пр, kpк, Ln. Lск, Lх в децибелах, Тш в кельвинах, и в секундах, ц в метрах квадратных.