Вопрос 4. Вычисление оценок коэффициентов регрессии.

Оценивание коэффициентов регрессии по методу наименьших квадратов

Для оценивания коэффициентов регрессии необходимы результаты Nнаблюдений, в ходе которых одновременно фиксируются значения входных и выходной переменных (матрицаХи вектор соответственно). По матрицеХвычисляют матрицуFзначений базисных функций в точках наблюдений.

- вектор оценок коэффициентов, полученных тем или иным способом из результатов наблюдений. Вектор значений выходной переменной, полученных по уравнению регрессии, есть

=F .

Введем ­вектор невязок, иливектор остатков.

Наиболее известный способ оценивания коэффициентов – метод наименьших квадратов (МНК). В этом методе ищут такую оценку , которая обеспечивает минимум суммы квадратов остатков:

=min.

В векторных обозначениях имеем:

==== === =.

Для поиска минимума требуется найти стационарные точки квадратичной по формы. Возьмем производную по вектору и приравниваем ее нулю:

=.

Получаем систему нормальных уравнений

. (3.2)

Согласно предпосылке 3 F’Fимеет обратную матрицу. Тогда

(3.3)

– вектор оценоккоэффициентов регрессии, полученных по методу наименьших квадратов (МНК-оценки).

Проиллюстрируем полученные соотношения применительно к парной регрессии, описываемой модельюДля нее

.

Система нормальных уравнений (3.2) примет вид:

Поделив первое уравнение системы на N,получим

, (а)

где ­ − средние значения наблюденных переменных («центр тяжести облака (диаграммы) рассеяния»). Поскольку(см. (3.28)), получаем, что точка () удовлетворяет уравнению

. (б)

Вычитая (а) из (б) и учитывая, что (см. (3.28)), приходим к уравнению регрессии «в отклонениях», не содержащему свободного члена. Полученный результат легко обобщается на случайnпеременных либоkбазисных функций.

Из (3.3) получаем, что

В (3.4) через обозначены средние квадратические отклонения. По найденной оценкеиз (а) находят.

Рассмотрим численный пример. Наблюдается объект, между выходом и входом которого имеется связь вида

. (3.5)

Исследователю модель (3.5) неизвестна, однако он располагает результатами четырех наблюдений над объектом (табл.9).

Таблица 9

i	x1i	x2i	y i
1	2	3	4	5
1	-1	-1	9	10
2	1	0	2	0
3	-1	1	7	7
4	1	2	4	5

Если бы случайные возмущения отсутствовали, то результатом наблюдений был бы столбец 4 (уⁱ). Полагая, что модель специфицирована в виде, найдем значения коэффициентов для этого случая:

.

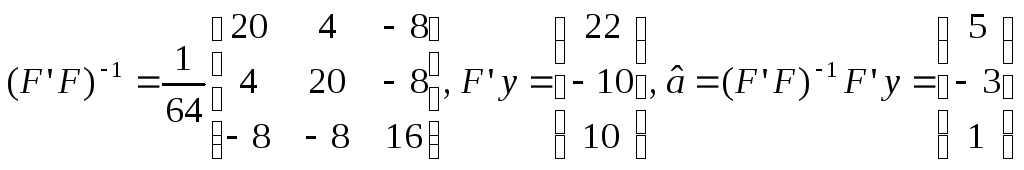Итак, в отсутствии возмущений МНК восстановил точные значения коэффициентов модели (3.5). Однако реально наблюдались значения столбца 5 (), так что

.

Вычисление оценок МНК не требует введения каких-либо дополнительных гипотез. Сам метод часто рассматривают как способ «разумного» выравнивания эмпирических данных. Однако судить об адекватности модели, о степени близости полученных оценок истинным значениям, об ее прогностической способности удается лишь за счет введения априорных сведений, зафиксированных в предпосылках классической регрессии.