Вопрос 28. Двойное экспоненциальное сглаживание.

Обобщим метод экспоненциального сглаживания на случай, когда модель процесса определяется линейной функцией a+bt. Как и прежде, при заданномминимизируется

.

(Здесь для удобства представления знаки иопущены.)

,

.

С учетом того что

,,

получаем

Процедуру вычисления можно рассматривать как сглаживание 1-го порядка. По аналогии строят сглаживание 2-го порядка:

.

Система уравнений примет вид:

Решая последнюю систему относительно а_tиb_t, получим:

;.

Далее

;

;

;

;

,

где – ошибка прогноза по линейной модели на один такт вперед.

Рассмотренную выше процедуру можно обобщить на случай полиномиальных трендов более высокого порядка (на практике не выше второго: y_t=a₀ + a₁t + a₂t²).

В описанных выше моделях содержался единственный параметр экспоненциального сглаживания β=1–α. Однопараметрические модели предложеныБрауном. Кроме модели Брауна известно несколько вариантов многопараметрических адаптивных моделей. Так, для линейно изменяющегося процесса часто используется двухпараметрическая модельХольта,в которой оценка коэффициентов производится следующим образом:

,

где α₁и α₂− параметры экспоненциального сглаживания, лежащие в диапазоне0–1. Адаптивность модели к новым данным наглядно видна, если ее переписать в виде:

,

где – ошибка прогноза на один такт вперед.

Вопрос 29. Дисперсия простой экспоненциальной средней.

2. Простое экспоненциальное сглаживание

Рассмотрим простейший ряд , равный сумме постояннойа(уровень) и случайной компоненты:

. (7.2)

Относительно возмущений полагаем, что они центрированы и некоррелированы, т.е. Mx_t= 0 и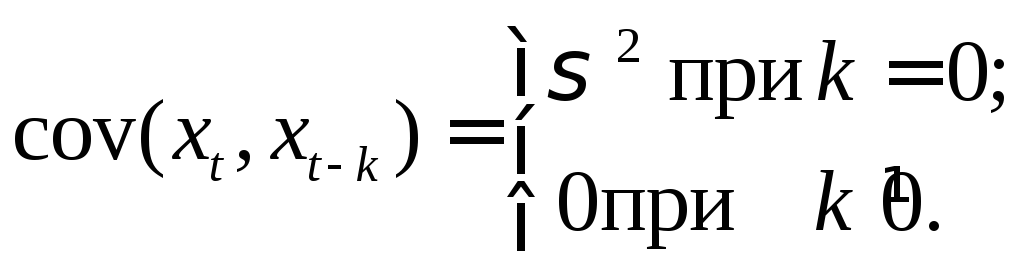

Будем считать, что ряд имеет бесконечную предысторию, т. е. время принимает значения t,t-1,t-2,...,-. Найдем оценкуа, воспользовавшись минимизацией взвешенной суммы квадратов:

.

Взяв производную по , проведем преобразования:

;

.

Полученную оценку ана моментtобозначим. Сглаженное значениеможно выразить через сглаженное значениев прошлый моментt-1 и новое наблюдение:

Полученное соотношение

перепишем несколько иначе, введя так называемую постоянную сглаживанияα=1–β (0 1):

. (7.3)

Из полученного соотношения видно, что новое сглаженное значение получается из предыдущего коррекцией последнего на долю ошибки, рассогласования, между новым и прошлым сглаженным (оно же, в соответствии с моделью ряда, и прогнозное) значениями ряда. Происходит своего рода адаптация уровня ряда к новым данным.

Для того чтобы удостовериться в «эффекте сглаживания», найдем дисперсию . С учетом модели ряда (7.2) имеем:

.

Отсюда и.

Полученные соотношения приводят к

.

Поскольку α≤ 1, дисперсия сглаженных значений оказывается меньше дисперсииσ²исходного ряда. Чем меньшеα, тем меньше дисперсия экспоненциальной средней. Вот почему экспоненциальное сглаживание часто интерпретируют как фильтр, на вход которого последовательно поступают члены исходного ряда, а на выходе формируются сглаженные значения. С уменьшениемαстепень фильтрации увеличивается, так как флуктуации ряда все более подавляются.

Для того чтобы воспользоваться рабочей формулой (7.3) в начальный момент t=1, необходимо знать. Обычно в качествеберут среднее арифметическое всех имеющихся точек либо нескольких от начала ряда.

Определенные сложности представляет проблема выбора постоянной сглаживания. В значительной мере этот выбор определяется целями исследования и конкретными свойствами ряда. Если сглаживание проводится с целью прогнозирования, то наилучшее значение αбудет зависеть от горизонта, иначе срока, прогнозированияτ. Для краткосрочных (конъюнктурных) прогнозов более актуальной является свежая информация, тогда как при большихτжелательно ослабить влияние конъюнктурных колебаний и в большей мере учитывать прошлые данные, увеличивая тем самым период ретроспекции. Введем понятие возраста данных, считая, что текущее наблюдение имеет возраст, равный нулю, возраст предыдущего наблюдения равен 1 и так далее. В качестве среднего значенияt_срвозраста данных примем сумму возрастов с весами, использованными для подсчета сглаженной величины:

Чем меньше α, тем больше средний возраст данных. Подбор конкретного значения αобычно осуществляют экспериментально среди возможных значений перебором на сетке от 0,1 до 0,9 с шагом 0,1. Используемый критерий здесь – минимум суммы квадратов отклонений между наблюденными и прогнозными значениями ряда. Напомним, что в соответствии с моделью ряда (7.2) ожидаемое прогнозное значение ряда на моментt+τ есть сглаженное значение ряда на моментt,т.е..