
- •Статистическое наблюдение. Сводка и группировка статистических данных
- •Тесты для самоподготовки
- •Задачи для самостоятельного решения
- •Абсолютные и относительные величины
- •Тесты для самоподготовки
- •Задачи для самостоятельного решения
- •Средние величины и показатели вариации
- •Показатели вариации
- •Виды дисперсий. Правило сложения дисперсий
- •Дисперсия альтернативного признака
- •Тесты для самоподготовки
- •Задачи для самостоятельного решения
- •Выборочное наблюдение
- •Тесты для самоподготовки
- •Задачи для самостоятельного решения
- •Ряды динамики
- •Тесты для самоподготовки
- •Задания для самостоятельного решения
- •Индексы
- •Тесты для самоподготовки
- •Задачи для самостоятельного решения
- •Статистические методы изучения взаимосвязей
- •Тесты для самоподготовки
- •Задачи для самостоятельного решения
- •394068, Г. Воронеж, ул. Хользунова, д. 40
Статистические методы изучения взаимосвязей
При статистическом исследовании корреляционных связей одной из основных задач является определение их формы, т.е. построение модели связи.
Построение регрессионной модели проходит несколько этапов: предварительный теоретический анализ, определение объекта, отбор факторов, сбор и подготовка данных, выбор модели связи, исчисление показателей тесноты корреляционной связи, оценка адекватности регрессионной модели.
Вычисление параметров корреляционных линейных уравнений по первичным данным. Если результативный признак с увеличением факторного признака равномерно возрастает или убывает, то такая зависимость является линейной и выражается уравнением прямой:
![]() , (1)
, (1)
где
![]() –
индивидуальные значения результативного
признака;
–
индивидуальные значения результативного
признака;
х – индивидуальные значения факторного признака;
и – параметры уравнения прямой (уравнения регрессии);
![]() –
теоретическое
значение результативного признака.
–
теоретическое
значение результативного признака.
Параметры уравнения прямой и определяются путем решения системы нормальных уравнений, полученных методом наименьших квадратов, или по формулам:
![]() (2)
(2)
![]() , (3)
, (3)
![]() . (4)
. (4)
Что касается параметра уравнения регрессии в виде свободного члена, то возможен и такой подсчет:
![]() . (5)
. (5)
В уравнении прямой параметр экономического смысла не имеет. Параметр является коэффициентом регрессии и показывает изменение результативного признака при изменении факторного признака на единицу. Часто исследуемые признаки имеют разные единицы измерения, поэтому для оценки влияния факторного признака на результативный применяется коэффициент эластичности. Он рассчитывается для каждой точки и в среднем по всей совокупности. Коэффициент эластичности (Э) определяется по формуле:
![]() ,
(6)
,
(6)
где
![]() – первая производная уравнения регрессии.
– первая производная уравнения регрессии.
Средний коэффициент эластичности определяется по формуле:
![]() . (7)
. (7)
Коэффициент эластичности показывает, на сколько процентов изменяется результативный признак при изменении факторного признака на 1%.
Определение параметров линейного однофакторного уравнения регрессии по сгруппированным данным. Если данные сгруппированы и представлены в виде корреляционной таблицы, то параметры линейного уравнения регрессии могут быть определены путем решения следующей системы нормальных уравнений:
![]() (8)
(8)
или по формулам
 (9)
(9)
 (10)
(10)
где
![]() –
групповые средние.
–
групповые средние.
Параметр уравнения регрессии можно определить также и по формуле (5).
Расчет параметров степенной функции. Если значения факторного признака расположены в порядке геометрической прогрессии и соответствующие значения результативного признака также образуют геометрическую прогрессию, то связь между признаками может быть представлена степенной функцией вида:
![]() (11)
(11)
Для определения параметров степенной функции методов наименьших квадратов необходимо привести ее к линейному виду путем логарифмирования:
![]() (12)
(12)
Система нормальных уравнений имеет вид:
![]() (13)
(13)
Параметры можно определить решая систему нормальных уравнений по формулам:
 (14)
(14)
![]() . (15)
. (15)
или
![]() (16)
(16)
![]() . (17)
. (17)
Параметр логарифмической функции является коэффициентом эластичности, который показывает, на сколько процентов изменяется результативный признак при изменении факторного признака на 1%.
Расчет параметров уравнения гиперболы. Если результативный признак с увеличением факторного признака возрастает (или убывает) не бесконечно, а стремится к конечному пределу, то для анализа такого признака применяется уравнение гиперболы вида:
![]() (18)
(18)
Для определения параметров этого уравнения используется система нормальных уравнений:
![]() . (19)
. (19)
Чтобы
определить параметры уравнения гиперболы
методом наименьших квадратов, необходимо
привести его к линейному виду. Для этого
произведем замену переменных:
![]() ,
получим следующую систему нормальных
уравнений:
,
получим следующую систему нормальных
уравнений:
![]() . (20)
. (20)
Параметры уравнения гиперболы можно вычислить по формулам:
 (21)
(21)
Статистические методы измерения тесноты корреляционной связи между двумя признаками. Одним из важнейших этапов исследования корреляционной связи является измерение ее тесноты. Для этого применяются: линейный коэффициент корреляции, теоретическое корреляционное отношение, индекс корреляции.
Линейный коэффициент корреляции применяется для измерения тесноты связи только при линейной форме связи:
 (22)
(22)
 (23)
(23)
![]() (24)
(24)
Теоретическое корреляционное отношение и индекс корреляции применяются для измерения тесноты корреляционной связи между признаками при любой форме связи, как линейной, так и нелинейной. Оба показателя можно вычислить только после того, как определена форма связи и исчислена теоретическая линия регрессии.
Теоретическое корреляционное отношение рассчитывается по формулам:
 (25)
(25)
 (26)
(26)
где
![]() – факторная дисперсия, которая
характеризует вариацию результативного
признака под влиянием признака–фактора,
включенного в модель;
– факторная дисперсия, которая
характеризует вариацию результативного
признака под влиянием признака–фактора,
включенного в модель;
![]() – общая
дисперсия, показывающая вариацию
результативного признака под влиянием
всех факторов, вызывающих эту вариацию.
– общая
дисперсия, показывающая вариацию
результативного признака под влиянием
всех факторов, вызывающих эту вариацию.
Теоретическое корреляционное отношение изменяется от 0 до 1; чем ближе корреляционное отношение к 1, тем теснее связь между признаками.
Для упрощения расчетов меры тесноты корреляционной связи часто применяется индекс корреляционной связи, который определяется по следующим формулам:
 (27)
(27)
 (28)
(28)
где
![]() – остаточная дисперсия, характеризующая
вариацию результативного признака под
влиянием прочих неучтенных факторов.
– остаточная дисперсия, характеризующая
вариацию результативного признака под
влиянием прочих неучтенных факторов.
Проверка адекватности однофакторной регрессионной модели и значимости показателей тесноты корреляционной связи. Адекватность регрессионной модели при малой выборке можно оценить F–критерием Фишера:
 , (29)
, (29)
где m – число параметров модели;
n – число единиц наблюдения.
Эмпирическое
значение критерия
![]() сравнивается
с критическим (табличным)
сравнивается
с критическим (табличным)
![]() с уровнем значимости 0,01 или 0,05 и числом
степеней свободы (m–1),
(n–m).
Если
с уровнем значимости 0,01 или 0,05 и числом
степеней свободы (m–1),
(n–m).
Если
![]() >
,
то уравнение регрессии признается
значимым.
>
,
то уравнение регрессии признается
значимым.
Значимость коэффициентов линейного уравнения регрессии и оценивается с помощью t–критерия Стьюдента (n<30):
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
Эмпирическое значение t–критерия сравнивается с критическим (табличным) значением t–распределения Стьюдента с уровнем значимости 0,01 или 0,05 и числом степеней свободы (n–2). Параметр признается значимым, если эмпирическое значение t больше табличного.
Аналогично проводится оценка коэффициента корреляции r с помощью t–критерия, который определяется по формуле:
![]() (33)
(33)
(n–2) – число степеней свободы.
Если эмпирическое значение t оказывается больше табличного, то линейный коэффициент корреляции признается значимым.
Пример7.1. Имеются выборочные данные по 10 однородным предприятиям:
Таблица 7.1
№ предприятия |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Электровооруженность труда на 1 рабочего, кВт/ч |
2 |
5 |
3 |
7 |
2 |
6 |
4 |
9 |
8 |
4 |
Выпуск готовой продукции на 1 рабочего, т. |
3 |
6 |
4 |
6 |
4 |
8 |
6 |
9 |
9 |
5 |
Построить однофакторную регрессионную модель.
Решение. Предположим, что между электровооруженностью труда и выпуском готовой продукции существует линейная корреляционная связь, которую можно выразить уравнением прямой вида .
Факторным признаком является электровооруженность труда, а результативным – выпуск готовой продукции.
Для
определения формы корреляционной связи
необходимо вычислить параметры уравнения
прямой путем решения системы нормальных
уравнений вида (2). Чтобы заполнить
систему нормальных уравнений фактическими
данными, необходимо определить
![]() ,
,
![]() ,
,
![]() .
.
Расчеты этих показателей представлены в таблице 7.2.
Таблица 7.2 – Расчет показателей для вычисления параметров уравнения прямой по несгруппированным данным
Исходные данные |
Расчетные значения |
||||||
№ предприятия |
Электровооруженность труда на 1 рабочего, кВт/ч |
Выпуск продукции на 1 рабочего, т. |
|
|
|
|
|
1 |
2 |
3 |
6 |
4 |
9 |
3,61 |
0,3721 |
2 |
5 |
6 |
30 |
25 |
36 |
6,01 |
0,0001 |
3 |
3 |
4 |
12 |
9 |
16 |
4,41 |
0,1682 |
… |
... |
... |
... |
... |
... |
... |
... |
9 |
8 |
9 |
72 |
64 |
81 |
8,38 |
0,381 |
10 |
4 |
5 |
20 |
16 |
25 |
5,20 |
0,04 |
Итого: |
50 |
60 |
343 |
304 |
400 |
60 |
5,761 |
В среднем: |
5,0 |
6,0 |
34,3 |
30,4 |
40,0 |
6,0 |
0,5761 |
Подставим в систему нормальных уравнений (2) фактические данные из таблицы 7.2 и получим равенства:
![]()
Систему нормальных уравнений решаем в такой последовательности (по методу множителей): умножим каждый член первого уравнения на 5:
![]()
Затем
вычтем из второго уравнения первое:
![]() .
Подставив полученное значение
в первое уравнение, получаем
.
Подставив полученное значение
в первое уравнение, получаем
![]() .
Уравнение регрессии имеет вид:
.
Уравнение регрессии имеет вид:
![]() .
.
С помощью определителей параметры уравнения прямой можно вычислить по формулам (3) и (4).
Если параметры регрессионного уравнения определены верно, то должно соблюдаться равенство сумм теоретических и эмпирических значений выпуска готовой продукции, а сумма разностей между эмпирическими и теоретическими значениями выпуска готовой продукции должна быть равна нулю.
Окончательную
проверку правильности расчета параметров
уравнения связи можно также произвести
подстановкой
![]() и
в систему нормальных уравнений
(рассматривая их как корни уравнения).
и
в систему нормальных уравнений
(рассматривая их как корни уравнения).
Используя
уравнение корреляционной связи, можно
определить теоретическое значение
![]() для
любой промежуточной точки (теоретическое
значение выпуска готовой продукции на
1 рабочего для любого промежуточного
значения электровооруженности труда
на 1 рабочего (см. табл. 7.1).
для
любой промежуточной точки (теоретическое
значение выпуска готовой продукции на
1 рабочего для любого промежуточного
значения электровооруженности труда
на 1 рабочего (см. табл. 7.1).
В
нашем уравнении регрессии параметр
![]() показывает, что с увеличением
электровооруженности труда 1 рабочего
на 1 кВт/ч выпуск готовой продукции
возрастет на 0,7963 т.
показывает, что с увеличением
электровооруженности труда 1 рабочего
на 1 кВт/ч выпуск готовой продукции
возрастет на 0,7963 т.
Средний коэффициент эластичности вычислим по формуле (7):
![]()
Коэффициент эластичности, равный 0,66, показывает, что с увеличением электровооруженности труда на 1% выпуск готовой продукции возрастет на 0,66%.
Измерим тесноту корреляционной связи между производительностью и электровооруженностью труда линейным коэффициентом корреляции, теоретическим корреляционным отношением, индексом корреляции (по формулам 23.26,28). Данные, необходимые для расчетов, представлены в таблице 7.1.

Для расчета теоретического корреляционного отношения необходимо предварительно вычислить дисперсии:
![]()
![]()
![]()
Теоретическое корреляционное отношение по формуле (25):
![]()
Коэффициент
детерминации
![]() равен 0,856. Индекс корреляции по формуле
(27):
равен 0,856. Индекс корреляции по формуле
(27):
![]()
Все показатели тесноты корреляционной связи показывают тесную связь между производительностью и электровооруженностью труда. Коэффициент детерминации 0.856 означает, что вариация выработки рабочих на 85,6% объясняется вариацией электровооруженности труда и на 14,4% – прочими факторами.
Так
как
![]() ,
то можно сделать заключение, что гипотеза
о линейной форме связи подтверждена.
,
то можно сделать заключение, что гипотеза
о линейной форме связи подтверждена.
Проведем оценку адекватности регрессионной модели с помощью F–критерия Фишера (формула 29)
![]()
Табличное значение с уровнем значимости 0.05 и числом степеней свободы (2–1), (10–2) равно 5,32. Так как > , уравнение регрессии можно признать адекватным.
Оценим значимость параметров уравнения регрессии с помощью t–критерия Стьюдента по формулам (30) и (31):
![]()
![]()
Значение
![]() вычисляется
по формуле (32):
вычисляется
по формуле (32):
![]()
Табличное значение t–критерия с уровнем значимости 0.05 и числом степеней свободы (n–2) равно 2,307.
Так
как
![]() >
>![]() ,
параметры уравнения регрессии можно
признать значимыми.
,
параметры уравнения регрессии можно
признать значимыми.
Значимость коэффициента корреляции оценим с помощью t–критерия по формуле (33):
![]()
Эмпирическое значение t больше табличного, следовательно, коэффициент корреляции можно признать значимым.
Вычислим
ошибку
аппроксимации
по формуле:
![]() .
.
![]()
Так как параметры уравнения регрессии значимы, уравнение значимо, показатели тесноты значимы, ошибка аппроксимации равна 5,8%, коэффициент детерминации равен 0,856, то можно сделать заключение, что построенная регрессионная модель зависимости производительности труда от его элекровооруженности может быть использована для анализа и прогноза.
Пример 7.2. Имеются данные по 52 предприятиям отрасли:
Таблица 7.3
Группы заводов по фондовооруженности, млн. руб. |
Количество заводов |
Объем продукции, млн. руб. |
5 – 7 |
1 |
3,0 |
7 – 9 |
2 |
5,0 |
9 – 11 |
3 |
6,3 |
... |
... |
... |
21 – 23 |
2 |
17,0 |
23 – 25 |
1 |
19,0 |
По исходным данным найти параметры линейного корреляционного уравнения, характеризующего зависимость между продукцией и фондовооруженностью.
Решение. Параметры линейного уравнения регрессии можно вычислить по формулам (9) и (10). Расчетные данные для вычисления параметров уравнения представлены в
таблице 7.4.
Таблица 7.4. – Расчет величин, необходимых для определения параметров уравнения прямой по сгруппированным данным
|
|
|
|
|
|
|
|
5 – 7 |
6 |
1 |
3,0 |
3,0 |
6 |
18,0 |
36 |
7 – 9 |
8 |
2 |
5,0 |
10,0 |
16 |
80,0 |
128 |
9 – 11 |
10 |
3 |
6,3 |
18,9 |
30 |
189,0 |
300 |
… |
... |
... |
... |
... |
... |
... |
... |
21 – 23 |
22 |
2 |
17,0 |
34,0 |
44 |
748,0 |
968 |
23 – 25 |
24 |
1 |
19,0 |
19,0 |
24 |
456,0 |
576 |
Итого: |
– |
52 |
– |
550,2 |
766 |
8641,2 |
11924 |
Расчетные данные из табл. 7.4 подставим в формулы (9) и (10):
![]() ;
;
![]()
Параметр показывает, что с ростом фондовооруженности на 1 млн. руб. объем произведенной продукции увеличивается на 0,838 млн. руб.
Уравнение
регрессии имеет вид:
![]() .
.
Пример 7.3. По 10 однородным магазинам имеются следующие данные:
Таблица 7.5
Товарооборот, тыс. руб. |
5 |
3 |
24 |
35 |
44 |
55 |
63 |
74 |
82 |
95 |
Товарные запасы, дни |
18 |
12 |
8 |
8 |
8 |
8 |
7 |
6 |
8 |
8 |
По исходным данным определить уравнение регрессии (связь гиперболическая) между товарооборотом и товарными запасами.
Решение. Для определения параметров уравнения гиперболы вида необходимо построить систему нормальных уравнений (19), (20) и методом определителей вычислить параметры уравнения по формулам (21). Расчетные данные для определения параметров уравнения гиперболы представлены в таблице 7.6.
Таблица 7.6. – Расчет величин, необходимых для определения параметров уравнения гиперболы
№ п/п |
Товарооборот, тыс. руб. |
Товарные запасы, дни |
|
|
|
|
1 |
5 |
18 |
0,2000 |
0,0400 |
3,6000 |
12,19 |
2 |
3 |
12 |
0,3333 |
0,1111 |
3,9996 |
15,35 |
3 |
24 |
8 |
0,0417 |
0,0017 |
0,3336 |
8,44 |
... |
... |
... |
... |
... |
... |
... |
9 |
82 |
8 |
0,0122 |
0,0001 |
0,0976 |
7,74 |
10 |
95 |
8 |
0,0105 |
0,0001 |
0,0840 |
7,69 |
Итого: |
480 |
91 |
0,6966 |
0,1550 |
8,8631 |
91,0 |
Подставив значения данных из табл. 7.6 в систему нормальных уравнений, получим
![]()
Вычислим параметры и по формулам (21), подставляя расчетные данные из табл. 8.3:

Уравнение регрессии имеет вид: .
Построение моделей связи в виде уравнения множественной регрессии. Изменение экономических явлений происходит под влиянием не одного, а большого числа самых разнообразных факторов. Связь между результативным признаком и двумя и более факторами принято выражать уравнением множественной регрессии.
Уравнения множественной регрессии могут быть линейные, криволинейные и комбинированные.
Наиболее простым видом уравнения множественной регрессии является линейное уравнение с двумя неизвестными переменными:
![]() (33)
(33)
Параметры уравнения множественной регрессии определяются методом наименьших квадратов путем системы нормальных уравнений:
 (34)
(34)
Параметры уравнения множественной регрессии показывают изменение результативного признака при изменении факторного признака на единицу. Для оценки влияния факторных признаков на результативный рассчитываются частные коэффициенты эластичности и бета–коэффициенты.
Частный коэффициент эластичности (Э) вычисляется по формуле:
![]() (35)
(35)
где
![]() – параметр при признаке–факторе;
– параметр при признаке–факторе;
![]() ,
,
![]() – средние значения факторного и
результативного признаков.
– средние значения факторного и
результативного признаков.
Частный коэффициент эластичности показывает, на сколько процентов изменяется результативный признак при измененеии факторного признака на 1% при фиксированных значениях других факторов.
Бета–коэффициент
(![]() )
вычисляется по формуле:
)
вычисляется по формуле:
![]() (36)
(36)
Бета–коэффициент показывает, как изменяется результативный признак при изменении факторного признака.
Сравнение бета–коэффициентов при различных факторах дает возможность оценить силу их воздействия на результативный признак.
Параметры уравнения регрессии можно определять по формулам через коэффициенты корреляции и средние квадратические отклонения:
![]() (37)
(37)
 (38)
(38)
 (39)
(39)
Парные коэффициенты корреляции можно вычислить по следующим формулам:
![]() (40)
(40)
![]() (41)
(41)
![]() (42)
(42)
Средние квадратические отклонения определяются по формулам:
![]() (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
Статистические методы измерения тесноты корреляционной связи в многофакторных моделях. При проведении многофакторного корреляционного анализа возникает необходимость расчета множественных, парных и частных коэффициентов корреляции. Для измерения тесноты корреляционной связи между результативным признаком и несколькими факторными при линейной форме связи рассчитывается множественный коэффициент корреляции по формуле:
 (46)
(46)
где
![]() ,
,![]() ,
,![]() – парные коэффициенты корреляции.
– парные коэффициенты корреляции.
Множественный коэффициент корреляции изменяется от 0 до +1. Он отражает тесноту корреляционной связи между результативным признаком и факторными признаками, включенными в уравнение множественной регрессии.
Парные коэффициенты корреляции вычисляются следующим образом:
![]() (47)
(47)
![]() (48)
(48)
 (49)
(49)
или по формулам (40), (41), (42).
Парные коэффициенты корреляции показывают тесноту корреляционной связи как между факторными и результативными признаками, так и между признаками–факторами.
Для исследования тесноты корреляционной связи между признаками при построении моделей множественной регрессии применяются частные (парные) коэффициенты корреляции, которые характеризуют тесноту корреляционной связи между факторным и результативным признаками, при элиминировании влияния учтенных факторов.
Частные коэффициенты корреляции вычисляются по формулам:
 (50)
(50)
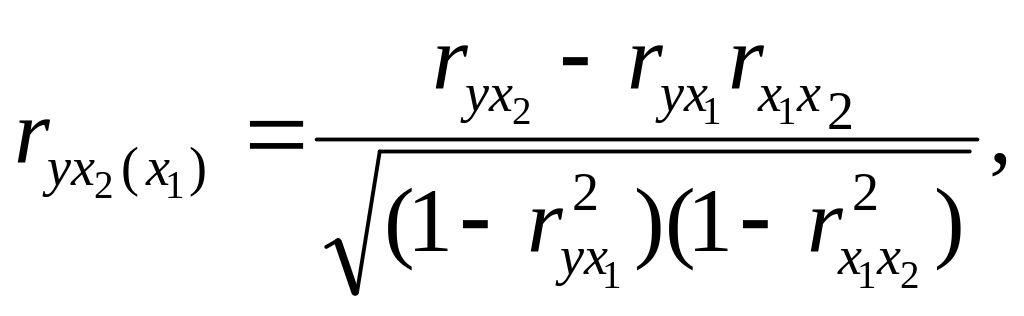 (51)
(51)
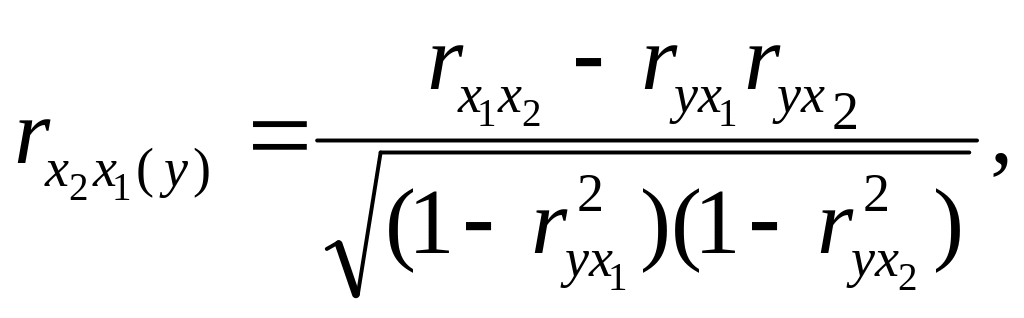 (52)
(52)
Теоретическое корреляционное отношение и совокупный индекс корреляции. Эти показатели имеют такой же экономический смысл, что при парной регрессии, и определяются по формулам
 (53)
(53)

Вместо теоретического корреляционного отношения может быть использован адекватный ему показатель – совокупный индекс корреляции:
 (54)
(54)

Проверка адекватности многофакторной регрессионной модели. Построенное уравнение множественной регрессии необходимо содержательно интерпретировать и оценить его с точки зрения адекватности реальной действительности. Прежде всего следует установить, соответствуют ли полученные данные тем гипотетическим представлениям, которые сложились в результате анализа, и показывают ли они причинно–следственные связи, которые ожидались.
Для оценки адекватности модели можно вычислить отклонение теоретических данных от эмпирических, остаточную дисперсию, а также ошибку аппроксимации, которая определяется по формуле
![]() (55)
(55)
Особое внимание необходимо обратить на интерпретацию и оценку параметров уравнения. Параметры уравнения регрессии следует проверить на их значимость.
Для оценки значимости параметров при малых выборках уравнения множественной регрессии используется t–критерий Стьюдента при (n–m–1) степенях свободы:
 (56)
(56)
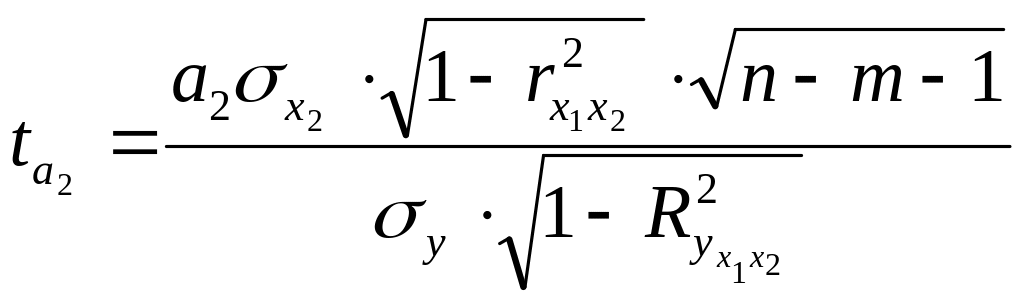 (57)
(57)
Значения
и
![]() берутся в абсолютном значении. Параметры
признаются значимыми, если
>
с уровнем значимости 0,05 и числом степеней
свободы (n–m–1).
берутся в абсолютном значении. Параметры
признаются значимыми, если
>
с уровнем значимости 0,05 и числом степеней
свободы (n–m–1).
Адекватность уравнения регрессии оценивается с помощью F–критерия Фишера, который определяется по формуле:
 (58)
(58)
Если > , то уравнение множественной регрессии признается значимым. Табличное значение FT определяется с уровнем значимости 0,01 или 0,05 и числом степеней свободы (m–1), (n–m).
Существенность совокупного коэффициента корреляции также оценивается с помощью t–критерия Стьюдента:
 (59)
(59)
Если > с заданным уровнем значимости 0,01 или 0.05 и числом степеней свободы (n–m–1), то коэффициент множественной корреляции признается значимым.
Пример 7.4. Имеются данные о выработке, продолжительности внутрисменных простоев и производственном стаже рабочих:
Таблица 7.7
№ рабочего |
Выработка продукции, т. |
Продолжительность внутрисменных простоев, мин. |
Производственный стаж, лет |
А |
1 |
2 |
3 |
1 |
39,0 |
19 |
4 |
2 |
38,7 |
15 |
3 |
3 |
38,9 |
17 |
4 |
Продолжение таблицы 7.7
А |
1 |
2 |
3 |
... |
... |
... |
... |
9 |
40,4 |
10 |
7 |
10 |
39,5 |
13 |
5 |
Итого: |
394 |
140 |
50 |
По исходным данным требуется построить уравнение множественной регрессии, характеризующее связь между выработкой, продолжительностью внутрисменных простоев и производственным стажем рабочих.
Решение.
Предположим,
что связь между исследуемыми признаками
линейная и уравнение регрессии имеет
вид:
![]() ,
где
,
где
![]() – продолжительность внутрисменных
простоев;
– продолжительность внутрисменных
простоев;
![]() – производственный
стаж рабочих;
– производственный
стаж рабочих;
– выработка изделий.
Параметры
уравнения множественной регрессии
определим по формулам (37), (38), (39). Произведем
расчет параметров уравнения множественной
регрессии, предварительно вычислив
![]() ,
,![]() ,
,![]() по формулам (43), (44), (45) (данные для их
расчета представлены в табл. 7.8).
по формулам (43), (44), (45) (данные для их
расчета представлены в табл. 7.8).
Таблица 7.8 – Расчетные данные
Исходные данные |
Расчетные данные |
|||||
№ рабочего |
Выработка, т.
|
Внутрисменные простои, мин. |
Производственный стаж, лет, |
|
|
|
1 |
39,0 |
19 |
4 |
1521 |
361 |
16 |
2 |
38,7 |
15 |
3 |
1497,69 |
225 |
9 |
3 |
38,9 |
17 |
4 |
1513,21 |
289 |
16 |
... |
... |
... |
... |
... |
... |
... |
9 |
40,4 |
10 |
7 |
1632.16 |
100 |
49 |
10 |
39,5 |
13 |
5 |
1560,25 |
169 |
25 |
Итого: |
394 |
140 |
50 |
15526,1 |
2030 |
264 |
В среднем: |
39,4 |
14 |
5 |
1552,61 |
203 |
26,4 |
![]()
![]()
![]()
Вычислим коэффициенты корреляции по формулам (40), (41), (42) (расчетные данные в табл. 7.9):
![]()
![]()
![]()
Таблица 7.9 – Расчетные данные
Исходные данные |
Расчетные данные |
|||||||
№ рабочего |
|
|
|
|
|
|
|
|
1 |
39,0 |
19 |
4 |
741 |
156 |
74 |
38,841 |
0,3721 |
2 |
38,7 |
15 |
3 |
580,5 |
116,1 |
45 |
38,912 |
0,0001 |
3 |
38,9 |
17 |
4 |
661,3 |
155,6 |
68 |
38,981 |
0,1681 |
... |
... |
... |
... |
... |
... |
... |
... |
... |
9 |
40,4 |
10 |
7 |
404 |
282,8 |
70 |
40,098 |
0,3844 |
10 |
39,5 |
13 |
5 |
513,5 |
197,5 |
65 |
39,470 |
0.04 |
Итого: |
394 |
140 |
50 |
5506,1 |
1974,6 |
676 |
394 |
5,763 |
В среднем: |
39,4 |
14 |
5 |
550,61 |
197,46 |
67,6 |
39,4 |
0,576 |
Рассчитаем значения параметров уравнения по формулам (37), (38), (39):
![]()
![]()
![]()
Уравнение
множественной регрессии имеет вид:
![]() .
.
Параметр
![]() показывает, что с увеличением внутрисменных
простоев на 1 мин. выработка продукции
снижается на 0,07 т.
показывает, что с увеличением внутрисменных
простоев на 1 мин. выработка продукции
снижается на 0,07 т.
Параметр
![]() показывает,
что с увеличением стажа рабочего на 1
год выработка продукции увеличивается
на 0,209 т.
показывает,
что с увеличением стажа рабочего на 1
год выработка продукции увеличивается
на 0,209 т.
Вычислим частный коэффициент эластичности по формуле (35):
![]() – с
увеличением простоев на 1% выработка
продукции снижается на 2,48%.
– с
увеличением простоев на 1% выработка
продукции снижается на 2,48%.
![]() – с
увеличением стажа на 1% выработка
увеличивается на 2,65%.
– с
увеличением стажа на 1% выработка
увеличивается на 2,65%.
Рассчитаем бета–коэффициенты по формуле (36):
![]() ;
;
![]() .
.
Анализ бета–коэффициентов показывает, что наиболее сильное влияние на производительность труда оказывает стаж рабочего.
Измерим
тесноту корреляционной связи между
выработкой рабочих, внутрисменными
простоями и стажем работы с помощью
парных коэффициентов корреляции. Эти
показатели, вычисленные ранее при
определении параметров уравнения
регрессии, равны:
![]()
![]()
![]()
Между выработкой и внутрисменными простоями существует тесная обратная корреляционная связь, между выработкой и стажем работы – тесная прямая связь. Коэффициенты парной корреляции отражают влияние на результативный признак не только исследуемого фактора, но и других, не включенных в модель факторов, которые связаны с исследуемым.
Для более точной оценки тесноты корреляционной связи вычислим частные коэффициенты корреляции по формулам (50), (51), (53)
![]()
![]()
![]()
Коэффициенты частной корреляции показывают, что влияние стажа на выработку рабочих, при исключении влияния внутрисменных простоев, меньше, чем при парной корреляции. Большое влияние на выработку оказывает стаж рабочих.
Вычислим множественный коэффициент корреляции по формуле (46):
![]()
Для измерения тесноты корреляционной связи между выработкой, простоем и стажем рабочего вычислим совокупный индекс корреляции по формуле (54):
![]()
Значения множественного коэффициента корреляции и индекса корреляции 0.869 и 0,812 свидетельствуют о наличии тесной корреляционной связи между выработкой, стажем и внутрисменными простоями, а расхождение между ними мене 0.1 подтверждает гипотезу о линейной форме связи.
Оценку
адекватности регрессионной модели
произведем с помощью F–критерия
Фишера. Для этого предварительно вычислим
факторную дисперсию по формуле:![]()
F–критерий
по формуле (58) равен:
![]()
Табличное значение с уровнем значимости 0,05 и числом степеней свободы 2 и 7 равно 4,74. Так как > , то уравнение регрессии можно признать адекватным.
Оценим значимость параметров уравнения множественной регрессии с помощью t–критерия Стьюдента по формулам (56) и (57)
![]()
![]()
Табличное значение t–критерия с уровнем значимости 0,05 и числом степеней свободы 6 равно 2,447. Так как < , то в отношении значимости параметров уравнения регрессии возникают сомнения.
Одной
из причин такой неопределенности
суждения относительно параметров
![]() и
является небольшое число наблюдений.
Эта величина должна превышать число
параметров в 6–7 раз, поэтому в данном
случае она должна составлять не менее
18 единиц.
и
является небольшое число наблюдений.
Эта величина должна превышать число
параметров в 6–7 раз, поэтому в данном
случае она должна составлять не менее
18 единиц.
Оценим значимость коэффициента множественной корреляции с помощью t–критерия Стьюдента по формуле (59):
![]()
Табличное значение t–критерия с уровнем значимости 0,05 и числом степеней свободы 6 равно 2,447. Так как > , коэффициент множественной корреляции можно признать значимым.
Коэффициент детерминации, равный 0,659, показывает, что вариация выработки на 65,9% объясняется вариацией внутрисменных простоев и стажем работы, а на 34,1% – прочими факторами.
Вычислим
среднюю ошибку аппроксимации:
![]() где
где
![]()
